leetcode2021年度刷题分类型总结(三)回溯法 (python)
主要参考:代码随想录
分为三个部分对回溯法进行总结
1.组合
例一:77. 组合
组合问题关键在于[1,4]和[4,1]算作重复答案,也即取数时往前推进,取到4时不能回头取1,所以每次都要记录取到的位置indx,并在下一循环中以这个位置作为循环的开始for i in range(indx,n):。还有就是剪枝时:
假设已经选择的元素个数:len(path)、那么还需要的元素个数为: k - len(path)。则在集合n中至多要从该起始位置 : n - (k - len(path)) + 1开始遍历,从大于n - (k - len(path)) + 1开始遍历会出现元素个数不足,没有必要遍历
例二:216. 组合总和 III
和例一同理,因为[1,3,5]和[5,3,1]的加和是一样的。只不过规定了取数的范围1-9,同样取数时往前推进,剪枝:
if sum(tmp)>n: #剪枝操作,元素总和如果已经大于n了,那么往后遍历就没有意义了
return
例三:17. 电话号码的字母组合
这题首先要进行一个数字到字母的映射,比较简单。重要的是它代表了不同集合之间的组合,而例一 例二都代表的是同一集合之间的组合。此时不用再记录在当前集合中的位置,而只用记录取到了第几个集合。
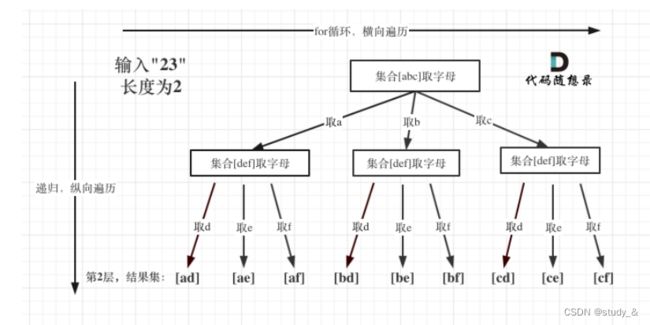
例四:39. 组合总和
同样还是组合问题,需要记录循环的起始位置for i in range(indx,len(candidates)),因为[2,2,3]和[3,2,2]被看作是重复的结果。
但是问题在于candidates 中的 同一个 数字可以 无限制重复被选取。 backtracking(candidates,target,i),把i传给下一次遍历而不是i+1,保证当前数可以被重复选取
规律
对于组合问题,什么时候需要startIndex来记录for循环的起始位置呢?(代码中用了indx)
如果是一个集合来求组合的话,就需要startIndex,例如:77.组合 (opens new window),216.组合总和III (opens new window),39. 组合总和
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17.电话号码的字母组合
2.子集
3.全排列
回溯算法的执行顺序 :当“衍生”的函数执行完后(可以是return,也可以是函数执行到了最后一句),回到之前函数的下一句,继续运行
组合
例一:77. 组合
77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
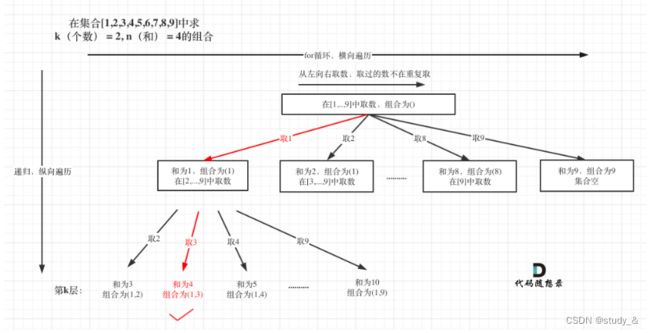
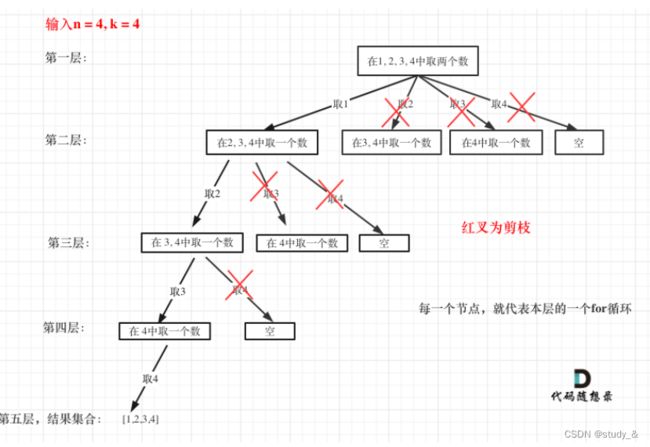
这题主要在于理解回溯算法的基本使用。以给出的n=4,k=2为例
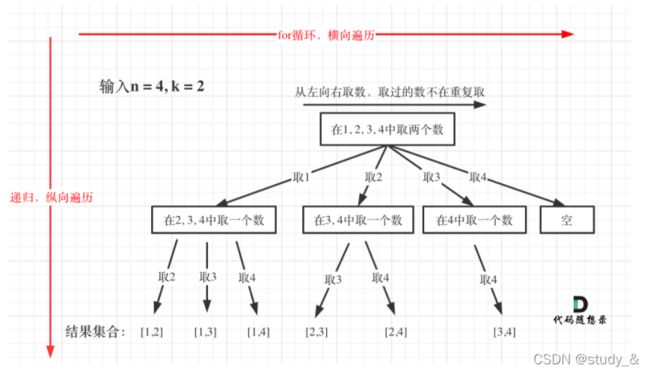
(上图来源:代码随想录)
由上图可知,代码的逻辑就是在递归中插入for循环遍历,一个递归循环的退出条件就是当path长度达到k。但是编码过程中容易出现一些小错误,比如我第一版的代码:
错误版本
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res=[]
path=[]
def dfs(n,k,indx):
if len(path)==k:
res.append(path)
return
for i in range(indx,n):
path.append(i)
dfs(n,k,i+1)
path.pop()
dfs(n,k,1)
return res
问题一出在res.append(path)这种写法是path的浅拷贝,每次path变化时res都会跟着变,所以最后得到的res是一个空数组,正确写法应该是res.append(path[:]);
问题二是for i in range(indx,n):这种写法导致path里面不会包含数字n,正确的写法应该是for i in range(indx,n+1):。之所以写成for i in range(indx,n):,是因为有点疑惑最后for循环里dfs(n,k,n+1)会得到什么,仔细想想若不满足len(path)==k的情况,由于此时indx是n+1也进不去for循环,dfs(n,k,n+1)自然跳过。
正确版本:
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res=[]
path=[]
def dfs(n,k,indx):
if len(path)==k:
res.append(path[:])
return
for i in range(indx,n+1):
path.append(i)
dfs(n,k,i+1)
path.pop()
dfs(n,k,1)
return res
上面的代码还有优化的空间,比如对于n=4,k=4这种情况,只有[1,2,3,4]这种情况符合要求,其他以2、3、4为起始位置的其他情况已经不足我们需要的元素个数了,所以就没有必要搜索了。对于这种情况可以用剪枝法来优化。
假设已经选择的元素个数:len(path)、那么还需要的元素个数为: k - len(path)。则在集合n中至多要从该起始位置 : n - (k - len(path)) + 1开始遍历,从大于n - (k - len(path)) + 1开始遍历会出现元素个数不足,没有必要遍历
(更仔细的说明:代码随想录)
剪枝优化版本:
这里需要注意取到n - (k - len(path)) + 1,所以写成n - (k - len(path)) + 2;
可以发现执行用时大大降低
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res=[]
path=[]
def dfs(n,k,indx):
if len(path)==k:
res.append(path[:])
return
for i in range(indx,n - (k - len(path)) + 2):
path.append(i)
dfs(n,k,i+1)
path.pop()
dfs(n,k,1)
return res
例二:216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
和77.组合同理
class Solution(object):
def combinationSum3(self, k, n):
"""
:type k: int
:type n: int
:rtype: List[List[int]]
"""
##只使用数字1到9
# k=2
# n=18
tmp=[]
res=[]
def backtracking(k,n,indx):
if sum(tmp)>n: #剪枝操作,元素总和如果已经大于n了,那么往后遍历就没有意义了
return
if k==0:
if sum(tmp)!=n:
return
else:
res.append(tmp[:])
return
if indx>9:
return
for i in range(indx,10): # (1,6)
tmp.append(i) # 1
backtracking(k-1,n,i+1)
tmp.pop()
backtracking(k,n,1)
# print(res)
return res
例三:17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
class Solution(object):
def letterCombinations(self, digits):
"""
:type digits: str
:rtype: List[str]
"""
def mapping(digit):
if digit=="2":
return list("abc")
if digit=="3":
return list("def")
if digit=="4":
return list("ghi")
if digit=="5":
return list("jkl")
if digit=="6":
return list("mno")
if digit=="7":
return list("pqrs")
if digit=="8":
return list("tuv")
if digit=="9":
return list("wxyz")
res=[]
tmp=[]
def backtracking(digits,n,indx):
if len(tmp)==n:
res.append("".join(tmp))
return
# if not digits: ##本来不应该运行到这里
# return
##原来版本:在回溯算法还有深度优先搜索算法中,谨慎用.pop(),因为函数出栈恢复环境的时候可不会把pop()掉的数重新补回来,这个时候还回到原来的地方pop()就会报错说不能对空list执行pop()
# digit=digits.pop()
digit=digits[indx]
opt=mapping(digit)
# print(opt)
for i in opt: ##
tmp.append(i) #d
backtracking(digits,n,indx+1) # "3" 2
tmp.pop()
digits=list(digits)
n=len(digits)
if n==0:
return []
backtracking(digits,n,0)
return res
回溯算法的执行顺序 :当“衍生”的函数执行完后(可以是return,也可以是函数执行到了最后一句),回到之前函数的下一句,继续运行
例四:39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
class Solution(object):
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
##重点之一:去重
## 刚开始循环写的是for candidate in candidates,没有记录for循环的起始位置
##这样会导致出现[2,2,3] [3,2,2]这类重复的答案
class Solution(object):
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
##重点之一:去重
## 刚开始循环写的是for candidate in candidates,没有记录for循环的起始位置
##这样会导致出现[2,2,3] [3,2,2]这类重复的答案
##原始版:每次backtracking都要求sum函数,sum函数时间复杂度O(n)
res=[]
tmp=[]
def backtracking(candidates,target,indx):
if sum(tmp)==target:
res.append(tmp[:])
return
if sum(tmp)>target:
return
for i in range(indx,len(candidates)):
tmp.append(candidates[i])
backtracking(candidates,target,i)##需要注意,还是要记录位置
tmp.pop()
backtracking(candidates,target,0)
return res
##优化版:sum函数用一个局部变量sum_代替,相比原始版时间近乎减半
res=[]
tmp=[]
def backtracking(candidates,target,indx,sum_):
if sum_==target:
res.append(tmp[:])
return
if sum_>target:
return
for i in range(indx,len(candidates)):
sum_+=candidates[i]
tmp.append(candidates[i])
backtracking(candidates,target,i,sum_)##需要注意,还是要记录位置
tmp.pop()
sum_-=candidates[i]
backtracking(candidates,target,0,0)
return res
##剪枝优化版:排序+剪枝
res=[]
tmp=[]
# sum_=0
def backtracking(candidates,target,indx,sum_):
if sum_==target:
res.append(tmp[:])
return
if sum_>target:
return
# 如果本层 sum + condidates[i] > target,就提前结束遍历,剪枝
for i in range(indx,len(candidates)):
if sum_ + candidates[i] > target:
return
sum_+=candidates[i]
tmp.append(candidates[i])
backtracking(candidates,target,i,sum_)##需要注意,还是要记录位置
tmp.pop()
sum_-=candidates[i]
# 为了剪枝需要提前进行排序
candidates.sort()
backtracking(candidates,target,0,0)
return res
剪枝优化版对比优化版来说加了排序+剪枝
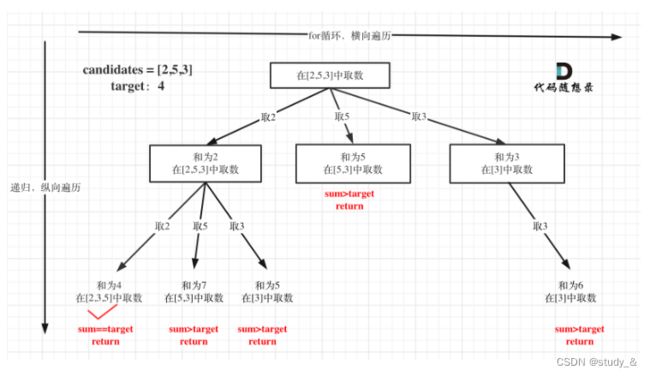
对比优化版,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。
那么可以在for循环的搜索范围上做做文章了。
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
但是要注意的是,这种剪枝不一定更高效,因为sort()函数也要耗费时间
优化版示意图
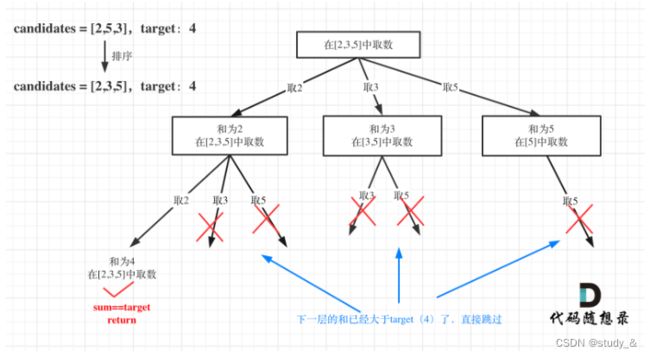
剪枝优化版示意图
例五:40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
class Solution(object):
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
#剪枝优化留着
#还是重复问题:之前的重复问题是startindx写错,导致有了[2,2,3]还会出现[3,2,2]
#现在的重复问题是数组本身有重复数据,需要排除重复数据影响
res=[]
tmp=[]
def backtracking(candidates,target,indx,sum_):
if sum_==target:
res.append(tmp[:])
return
if sum_>target:
return
for i in range(indx,len(candidates)):
if i!=indx: ##去除重复的组合
if candidates[i]==candidates[i-1]:
continue
# 剪枝,同39.组合总和
if sum_ + candidates[i] > target:
return
sum_+=candidates[i]
tmp.append(candidates[i])
backtracking(candidates,target,i+1,sum_)
sum_-=candidates[i]
tmp.pop()
candidates.sort()# 必须提前进行数组排序,避免重复
backtracking(candidates,target,0,0)
return res
说明:
这题最难的地方在于去重,我使用的去重逻辑是
candidates.sort()# 必须提前进行数组排序,避免重复
还有在循环时
if i!=indx: ##去除重复的组合
if candidates[i]==candidates[i-1]:
continue
原理是对同一树层使用过的元素进行跳过。if i!=indx用来确定是同一树层,否则后续candidates[i-1]可能跳回到上一树层;if candidates[i]==candidates[i-1]用来判断是同一树层的相同数,continue跳过
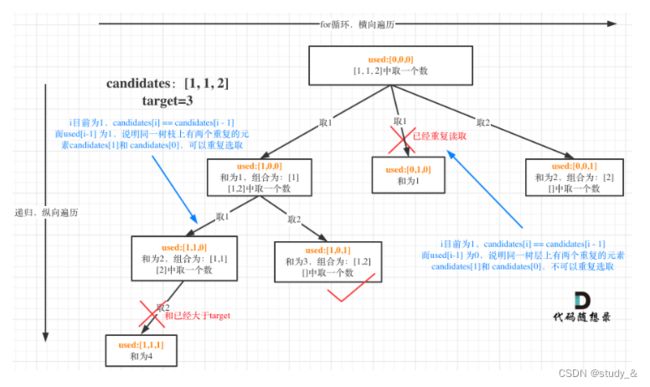
更详细的说明:代码随想录
子集
例六.131. 分割回文串
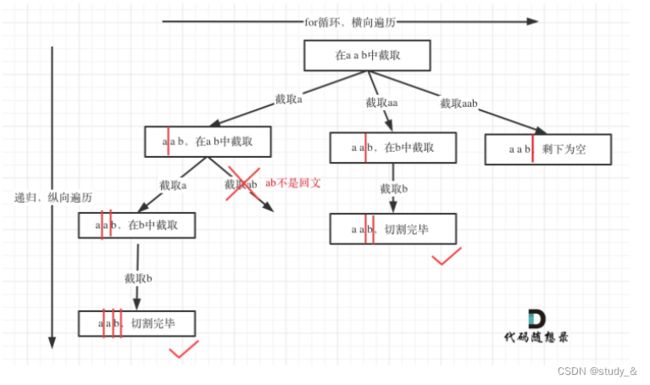
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
class Solution(object):
def partition(self, s):
"""
:type s: str
:rtype: List[List[str]]
"""
##回溯+函数判断回文串
res=[]
tmp=[]
# s=list(s)
def isreverse(ss):
left,right=0,len(ss)-1
while left<right:
if ss[left]==ss[right]:
left+=1
right-=1
else:
return False
return True
def backtracking(s,indx,n):
if indx>=n:
res.append(tmp[:])
return
for i in range(indx,n):
if isreverse(s[indx:i+1]):
tmp.append(s[indx:i+1])
backtracking(s,i+1,n)
tmp.pop()
backtracking(s,0,len(s))
return res
##回溯+正反序判断回文串
res=[]
tmp=[]
def backtracking(s,indx,n):
if indx>=n:
res.append(tmp[:])
return
for i in range(indx,n):
ss=s[indx:i+1]
if ss==ss[::-1]:
tmp.append(s[indx:i+1])
backtracking(s,i+1,n)
tmp.pop()
backtracking(s,0,len(s))
return res
例七.93. 复原 IP 地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。
例如:“0.1.2.201” 和 “192.168.1.1” 是 有效 IP 地址,但是 “0.011.255.245”、“192.168.1.312” 和 “[email protected]” 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 ‘.’ 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
输入:s = “25525511135”
输出:[“255.255.11.135”,“255.255.111.35”]
class Solution(object):
def restoreIpAddresses(self, s):
"""
:type s: str
:rtype: List[str]
"""
##探讨下0的情况
res=[]
tmp=[]
n=len(s)
if n>12: ##字符多于12个时不会有解
return []
def backtracking(s,indx):
if len(tmp)==4 and indx>=n:
res.append(".".join(tmp[:]))
return
if len(tmp)>4: #
return
for i in range(indx,n):
string=s[indx:i+1]
if string != "0" and string.lstrip('0') != string: #Python lstrip() 方法用于截掉字符串左边的空格或指定字符。
continue
#这个部分说明string != "0"且左边存在'0',比如“01”这种含有前导 0的例子,此时continue代表跳过
if int(string)>=0 and int(string)<=255:
tmp.append(s[indx:i+1])
backtracking(s,i+1)
tmp.pop()
backtracking(s,0)
return res
例八:78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
#去重
res=[]
tmp=[]
n=len(nums)
res.append([])
def backtracking(indx,n):
if indx>=n:
# res.append(tmp[:])
return
for i in range(indx,n):
tmp.append(nums[i])
res.append(tmp[:])
backtracking(i+1,n)
tmp.pop()
backtracking(0,n)
return res
说明:
一样的框架和步骤,只不过换成把中间的过程值当成结果存起来
例九:90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
class Solution(object):
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
#跟子集问题比较起来,需要去下重
res=[]
tmp=[]
n=len(nums)
nums.sort()
res.append([])
def backtracking(indx,n):
if indx>=n:
return
for i in range(indx,n):
if i!=indx:
if nums[i]==nums[i-1]:
continue
tmp.append(nums[i])
res.append(tmp[:])
backtracking(i+1,n)
tmp.pop()
backtracking(0,n)
return res
说明
跟78.子集问题比较,多了一个去重的步骤,这个去重的步骤和40.组合总和问题的去重方法一致,对同一树层使用过的元素进行跳过
if i!=indx: ##去除重复的组合
if candidates[i]==candidates[i-1]:
continue
原理是对同一树层使用过的元素进行跳过。if i!=indx用来确定是同一树层,否则后续candidates[i-1]可能跳回到上一树层;if candidates[i]==candidates[i-1]用来判断是同一树层的相同数,continue跳过
例十:491. 递增子序列
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
输入:nums = [4,6,7,7]
输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
class Solution(object):
def findSubsequences(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
##本题首先不能排序,因为要求不同的递增子序列
##同时要关注重复元素的去重,难点在怎么去除
##此时可以引入额外的数组来记录
## 同一父节点下的同层上使用过的元素就不能在使用了
res=[]
tmp=[]
n=len(nums)
def backtracking(indx,n):
if indx>=n:
return
store=[]
for i in range(indx,n):
if nums[i] not in store:
store.append(nums[i])
else:
continue
if tmp:
if nums[i]>=tmp[-1]:
tmp.append(nums[i])
else:
continue
else:
tmp.append(nums[i])
if len(tmp)>=2:
res.append(tmp[:])
backtracking(i+1,n)
tmp.pop()
backtracking(0,n)
return res
说明
##本题首先不能排序,因为要求不同的递增子序列
##同时要关注重复元素的去重,同一父节点下的同层上使用过的元素就不能在使用了,难点在怎么去除
##此时可以引入额外的数组来记录
## # 深度遍历中每一层都会有一个全新的store数组用于记录本层元素是否重复使用
全排列
例十一:46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res=[]
tmp=[]
n=len(nums)
def backtracking(n):
if len(tmp)==n:
res.append(tmp[:])
return
for i in range(n):
if nums[i] in tmp:
continue
tmp.append(nums[i])
backtracking(n)
tmp.pop()
backtracking(n)
return res
说明:
此时由于是求全排列,不用再记录在集合当中的位置。以nums = [1,2,3]为例,
for i in range(n):
tmp.append(nums[i])
backtracking(n)
tmp.pop()
可以得到有重复元素的全排列
[[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]]
按照题目要求,需要去掉[[1,1,1],[1,1,2],[1,1,3]等有重复元素的答案,所以添加条件
if nums[i] in tmp:
continue
例十二:47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
## 有逻辑错误的版本
res=[]
tmp=[]
n=len(nums)
used=[]
def backtracking(n):
if len(tmp)==n:
res.append(tmp[:])
return
store=[]#去除同层同元素的重复
for i in range(n):
if i in used: #在一种可能的组合中,用过的元素在下一次列举中不能再用
continue
if i in store:
continue
tmp.append(nums[i])
used.append(i)
store.append(i)
backtracking(n)
tmp.pop()
used.pop()
backtracking(n)
return res
## 正确的版本
res=[]
tmp=[]
n=len(nums)
used=[]
def backtracking(n):
if len(tmp)==n:
res.append(tmp[:])
return
store=[]#去除同层同元素的重复
for i in range(n):
if i in used: #在一种可能的组合中,用过的元素zia不能再用
continue
if nums[i] not in store:
store.append(nums[i])
else:
continue
tmp.append(nums[i])
used.append(i)
backtracking(n)
tmp.pop()
used.pop()
backtracking(n)
return res
说明:
这题的难点同样在于去重,而且分为两类去重,一类是#去除同层同值元素的重复,一类是#在一种可能的组合中,用过的元素在下一次列举中不能再用。分别用store和used数组记录同层同值元素 和用过的元素位置(防止在下一次列举中再次用到此元素)。store存的是元素值,used存的是元素位置。
以[1,1,2]为例加以说明,used数组是为了防止出现[1,1,1]之类答案,即多次使用同一元素;store数组是为了防止出现[1,1,2] [1,1,2]之类因为数组中下标0,1位置是相同元素而出现的重复答案
例二:306. 累加数
306. 累加数
这题和上一题是同样的逻辑,但是相比上一题更绕脑子。
首先分个三步走:
一、需要确定的变量。
num一定需要;用于指向当前所在数字的索引index;
数当前是第几个可行数的count(只有count>2,才符合累加数的条件);
还有就是指向前前个数的prevprev和前个数的prev,还有当前正在确定的数current
二、单层逻辑
先假设当前数current是0,i从指向当前所在数字的索引index取到len(num),把num[i]转成int,尝试附在current后,current=current*10+int(num[i])。在有效数大于等于两个时,即count>=2时,如果当前current<(prevprev+prev),说明当前取的数还不够大,有可能是需要取到下一个数,所以继续循环;如果current>(prevprev+prev),说明当前数不合格,直接return False。
而在count<2或者current==(prevprev+prev)的情况,则需要判断if dfs(num,i+1,count+1,prev,current)
以“199100”为例,如果count<2,先把初始数“1”当作独立的一个数,然后再把之后的“9”当作独立的一个数,prevprev=1,prev=9,current=9,此时current>(prevprev+prev),所以return False,即dfs(num,2,2,9,9)为False,for循环继续,current变成99,继续往下
current==(prevprev+prev)的情况,继续往下搜
三、退出递归的条件
当index>=len(num)且count>2,说明得以正常退出,return True
如果到了index>=len(num),还不满足有效数大于2,return False(比如"19910")
class Solution(object):
def isAdditiveNumber(self, num):
"""
:type num: str
:rtype: bool
"""
n=len(num)
# if n<3:
# return False
def dfs(num,index,count,prevprev,prev):
if index>=len(num):
if count>2:
return True
else:
return False
# return count>2
current=0
for i in range(index,len(num)):
c=num[i]
if num[index]=='0' and i>index:
return False
current=current*10+int(c)
if count>=2:
if current>(prevprev+prev):
return False
if current<(prevprev+prev):
continue
if dfs(num,i+1,count+1,prev,current):
return True
return False
return dfs(num,0,0,0,0)
例三:1980. 找出不同的二进制字符串
1980. 找出不同的二进制字符串
这题之前做的时候是直接暴力解决的,也能过,就是时间消耗大。
首先,如果n==2**length,说明表中互不相同 的二进制字符串齐全了,返回None
否则,首先生成n位二进制的全排列,如果全排列中的数在num中不存在,就可以作为答案
方法一:暴力解法
def findNearstZero(temp,n,perm):
for i in range(n-2,-1,-1):
if temp[i]=='0':
temp[i]='1'
for j in range(i + 1, n):
temp[j]='0'
perm.append(''.join(temp))
break
class Solution(object):
def findDifferentBinaryString(self, nums):
"""
:type nums: List[str]
:rtype: str
"""
n=len(nums)
length=len(nums[0])
if n==2**length:
return None
#生成n位二进制的全排列
perm=[]
temp=""
for i in range(length):
temp=temp+"0"
perm.append(temp) #初始化temp\perm为length长个0
temp = list(temp)
# # #生成具有n长,所有元素的哈希表
for i in range(2**length):
if temp[length-1]=='0':
temp[length-1]='1'
perm.append(''.join(temp)) #首先把最末尾的数字变1,放到perm中去
else:
findNearstZero(temp,length,perm) #如果最末尾已经是1了,在往前找最靠近末尾的0,把它翻成1,并把结果放在perm中
for j in perm: #如果全排列中的数在num中不存在,就可以作为答案
if j not in nums:
return j
当然,上面的代码可以进一步优化,比如不用perm把每一次排列的结果存起来,而是每次得到一个可行的排列数,就判断它是否在nums中。但是由于重点是回溯法,就不改了
方法二:回溯法
这题和例一非常相似,只改了for循环的次数和退出条件。
for循环:由于横向遍历每次都只用在0,1中选一个数,所以写成for i in range(2);
退出条件:depth作为深度搜索的输入变量,刚开始depth=0,之后每取一个数depth+1,depth用于判断一个字段是否足够长度,或者当path的长度达到length也可以判断一个字段是否足够长度,所以depth==length and len(path)==length可以只选用一个作为判断条件,因为两者同时达到要求。tmp用来记录生成的每个字段,比如如果nums=[“00”,“01”],tmp会依次变成“00”、“01”、“10”,到“10”时,由于tmp not in nums,所以return tmp
!!!这里要注意,return tmp不是return 到dfs(0),而是return 到dfs(2),所以需要用returnnum接住dfs(2)的返回值,再返回到dfs(0)
class Solution(object):
def findDifferentBinaryString(self, nums):
"""
:type nums: List[str]
:rtype: str
"""
n=len(nums)
length=len(nums[0])
if n==(1<<length):
return None
path=[]
# nums_compet=[] #生成n位二进制的全排列
def dfs(depth):
if depth==length and len(path)==length:
# print(path)
tmp=""
for k in path:
tmp+="".join(str(k))
# print(tmp)
if tmp not in nums:
return tmp
# nums_compet.append(path[:])
return
for i in range(2):
path.append(i)
returnnum=dfs(depth+1)
if returnnum!=None:
return returnnum
path.pop()
return dfs(0)
例四:2151. 基于陈述统计最多好人数
2151. 基于陈述统计最多好人数
方法一:二进制枚举
二进制遍历各种好人和坏人的可能性,然后提取出预设正确的中,好人数最多的预设
i代表对好人和坏人的一种预设,假设1代表好人,0代表坏人,从000……0到111……1 (长度为len(statements)),一共有2**len(statements)种可能。
只要存在二进制预设的真实值和提供的statements不符和,则预设错误 (any函数);否则预设正确,好人数加一;
返回正确预设中的最大好人数。
class Solution(object):
def maximumGood(self, statements):
"""
:type statements: List[List[int]]
:rtype: int
"""
def check(i):
cnt=0
for j,row in enumerate(statements):
if (i>>j)&1:
if any((st<2 and st!=(i>>k)&1) for k,st in enumerate(row)):
return 0 #只要存在二进制预设的真实值和提供的statements不符和,则预设错误 (any函数)
cnt+=1 #否则预设正确,好人数加一
return cnt #返回最大好人数
return max(check(i) for i in range(1,1<<len(statements)))#返回正确的二进制预设中,好人数最多的预设
代码参考自力扣题解
需要注意的地方有 1<
还有 (i>>j)&1 ,i>>j表示i(二进制表示)右移j位,左边空出的位补0;(i>>j)&1表示取出 i 二进制中第 j 位的值。也即表示取出第j个人是好人还是坏人的标志
方法二:回溯法
待补充
参考
【1】力扣
【2】代码随想录