LRU缓存机制(包含流程图分析以及各操作的解析详解)
LRU缓存机制
-
- 一、题目需求
- 二、LRU缓存机制的概念
- 三、LRU缓存机制的代码示例
- 四、LRU缓存机制的分析
-
- (一)、内部类CacheNode
- (二)、内部变量
- (三)、get()操作
- (四)、put()操作
- (五)、移动操作
- 五、流程图
一、题目需求
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果关键字 (key) 存在于缓存中,则获取关键字的值(总是正数),否则返回 -1。
写入数据 put(key, value) - 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字/值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得关键字 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得关键字 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
二、LRU缓存机制的概念
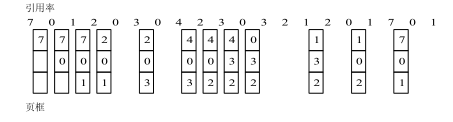
LRU是Least Recently Used的缩写,即最近最少使用,是一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段,用来记录一个页面自上次被访问以来所经历的时间 t,当须淘汰一个页面时,选择现有页面中其 t 值最大的,即最近最少使用的页面予以淘汰。
最近最少使用算法(LRU)是大部分操作系统为最大化页面命中率而广泛采用的一种页面置换算法。该算法的思路是,发生缺页中断时,选择未使用时间最长的页面置换出去。 [1] 从程序运行的原理来看,最近最少使用算法是比较接近理想的一种页面置换算法,这种算法既充分利用了内存中页面调用的历史信息,又正确反映了程序的局部问题。利用
LRU 算法对上例进行页面置换的结果如图1所示。当进程第一次对页面 2 进行访问时,由于页面 7 是最近最久未被访问的,故将它置换出去。当进程第一次对页面 3进行访问时,第 1 页成为最近最久未使用的页,将它换出。由图1可以看出,前 5 个时间的图像与最佳置换算法时的相同,但这并非是必然的结果。因为,最佳置换算法是从“向后看”的观点出发的,即它是依据以后各页的使用情况;而 LRU 算法则是“向前看”的,即根据各页以前的使用情况来判断,而页面过去和未来的走向之间并无必然的联系。
三、LRU缓存机制的代码示例
public class LRUCache {
private class CacheNode {
private CacheNode prev;
private CacheNode next;
private int key;
private int value;
public CacheNode(int key, int value) {
this.key = key;
this.value = value;
this.prev = null;
this.next = null;
}
}
private int capacity;
private HashMap<Integer, CacheNode> valNodeMap = new HashMap<>();
private CacheNode head = new CacheNode(-1, -1);
private CacheNode tail = new CacheNode(-1, -1);
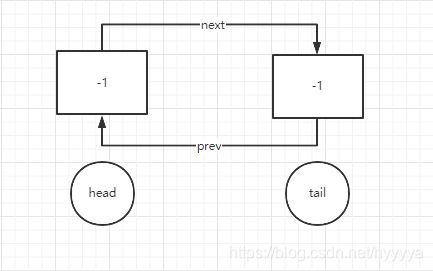
public LRUCache(int capacity) {
this.capacity = capacity;
head.next = tail;
tail.prev = head;
}
public int get(int key) {
if (!valNodeMap.containsKey(key)) {
return -1;
}
CacheNode current = valNodeMap.get(key);
current.prev.next = current.next;
current.next.prev = current.prev;
moveToTail(current);
return valNodeMap.get(key).value;
}
public void put(int key, int value) {
if (get(key) != -1) {
valNodeMap.get(key).value = value;
return;
}
if (valNodeMap.size() == capacity) {
valNodeMap.remove(head.next.key);
head.next = head.next.next;
head.next.prev = head;
}
CacheNode node = new CacheNode(key, value);
valNodeMap.put(key, node);
moveToTail(node);
}
private void moveToTail(CacheNode node) {
node.prev = tail.prev;
tail.prev = node;
node.next = tail;
node.prev.next = node;
}
}
四、LRU缓存机制的分析
(一)、内部类CacheNode
设置内部类CacheNode,由于题目要求put()操作为O(1)的时间复杂度,所以通过指针的方式,可实现数据的添加以及当达到缓存上限时移除最近最少使用的数据,添加新的数据的操作。
private class CacheNode {
private CacheNode prev;
private CacheNode next;
private int key;
private int value;
public CacheNode(int key, int value) {
this.key = key;
this.value = value;
this.prev = null;
this.next = null;
}
}
(二)、内部变量
capacity:表明当前的缓存上限。
valNodeMap:通过HashMap的数据结构,可实现get()和put()数据的时间复制度都为O(1)。
head:作为头节点,方便定位
tail:作为尾节点,方便定位
private int capacity;
private HashMap<Integer, CacheNode> valNodeMap = new HashMap<>();
private CacheNode head = new CacheNode(-1, -1);
private CacheNode tail = new CacheNode(-1, -1);
(三)、get()操作
首先判断该key是否存在HashMap缓存中,如果不在,根据题目要求返回-1。
如果该key存在,则调整其位置,将其移至尾巴节点的前一节点位置。同时改变该节点的前后两个节点的next指针和prev指针的指向目标。
public int get(int key) {
if (!valNodeMap.containsKey(key)) {
return -1;
}
CacheNode current = valNodeMap.get(key);
current.prev.next = current.next;
current.next.prev = current.prev;
moveToTail(current);
return valNodeMap.get(key).value;
}
(四)、put()操作
首先判断该key是否存在缓存中,如果存在。则进行重新赋值操作。由于get()操作中便将该节点的位置进行了调整,所以无须进行调整操作。
如果不在缓存中,则判断是否到达缓存上限。如果达到缓存上限,则将头节点的下一节点移除。并将该节点置于尾节点的前一节点位置。
public void put(int key, int value) {
if (get(key) != -1) {
valNodeMap.get(key).value = value;
return;
}
if (valNodeMap.size() == capacity) {
valNodeMap.remove(head.next.key);
head.next = head.next.next;
head.next.prev = head;
}
CacheNode node = new CacheNode(key, value);
valNodeMap.put(key, node);
moveToTail(node);
}
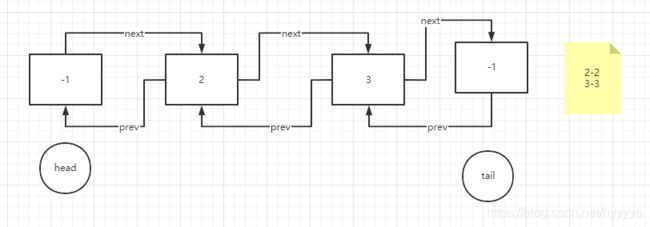
(五)、移动操作
只是简单的进行指针的重新指向,使得该节点插入到尾节点的前一位置。
private void moveToTail(CacheNode node) {
node.prev = tail.prev;
tail.prev = node;
node.next = tail;
node.prev.next = node;
}
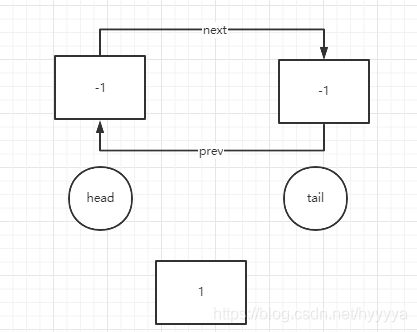
五、流程图
1、初始状态
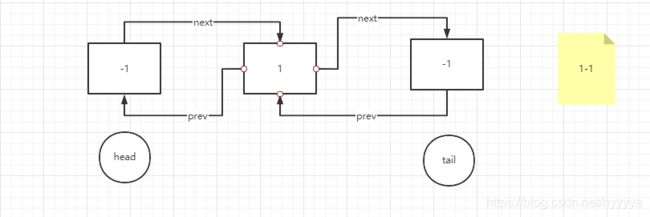
4、开始插入第二个节点
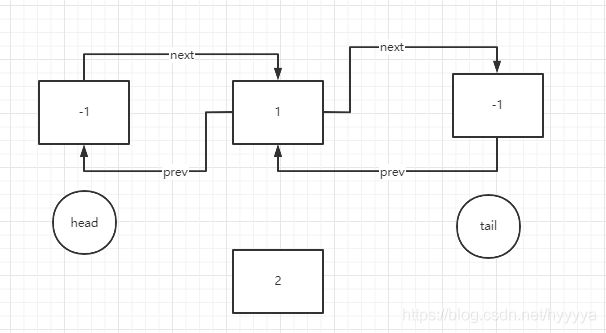
5、插入完毕,并且存入缓存Map(已到达缓存上限)
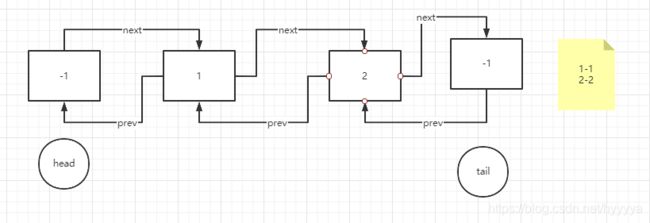
6、插入新的节点(已到达缓存上限)
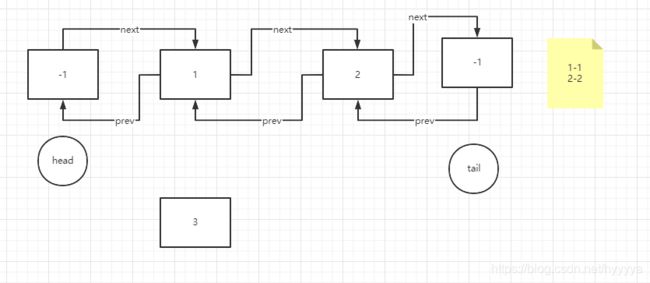
7、插入完毕,同时1号节点已被移除出缓存,并且2号节点的位置被调整