西瓜书+南瓜树第八章 集成学习
集成学习
- 8.1 个体与集成
- 8.2 Boosting
-
- 8.2.1Boosting介绍
- 8.2.2AdaBoost算法
- 8.3Bagging与随机森林
-
- 8.3.1Bagging
- 8.3.2 随机森林
- 8.4多样性增强
8.1 个体与集成
集合个体应该和而不同,
①和指个体学习器的泛化误差应该小于随机误差,以二分类问题为例,就是指误差 ϵ \epsilon ϵ<0.5
②不同指的是,个体学习器之间应该有所差异,这样集成学习才有意义
收敛条件的两个结论:
①个体学习器越多越好,能降低集成错误率
② ϵ ≠ \epsilon\neq ϵ= 0.5
8.2 Boosting
8.2.1Boosting介绍
Boosting是一族可将弱学习器提升为强学习器的算法,这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器的数目达到事先指定的指T,最终将这T个基学习器进行加权结合。
8.2.2AdaBoost算法
Boosting族最著名的代表是AdaBoost,其描述如下图所示,其中 y i ∈ { − 1 , 1 } , f y_i\in\{-1,1\},f yi∈{−1,1},f是真值函数。

AdaBoost算法有多种推导方式,比较容易理解的是基于“加性模型”,即基学习的线性组合
H ( x ) = ∑ t = 1 T a t h t ( x ) H(x)=\sum_{t=1}^{T}a_th_t(x) H(x)=t=1∑Tatht(x)
来最小化指数损失函数
ℓ exp ( H ∣ D ) = E x ∼ D [ e − f ( x ) H ( x ) ] \ell_{\exp}(H|D)=\mathbb{E}_{x\thicksim D}[e^{-f(x)H(x)}] ℓexp(H∣D)=Ex∼D[e−f(x)H(x)]
若 H ( x ) H(x) H(x)令指数损失函数最小化,则考虑损失函数对其的偏导
∂ ℓ exp ( H ∣ D ) ∂ H ( x ) = 1 2 l n P ( f ( x ) = 1 ∣ x ) P ( f ( x ) = − 1 ∣ x ) , \frac{\partial\ell_{\exp}(H|D)}{\partial H(x)}=\frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)}, ∂H(x)∂ℓexp(H∣D)=21lnP(f(x)=−1∣x)P(f(x)=1∣x),因此,有
s i g n ( H ( x ) ) = s i g n ( 1 2 l n P ( f ( x ) = 1 ∣ x ) P ( f ( x ) = − 1 ∣ x ) ) = arg max y ∈ { − 1 , 1 } P ( f ( x ) = y ∣ x ) sign(H(x))=sign(\frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)}) \\ =\argmax_{y \in\{-1,1\}}P(f(x)=y|x) sign(H(x))=sign(21lnP(f(x)=−1∣x)P(f(x)=1∣x))=y∈{−1,1}argmaxP(f(x)=y∣x)
这意味着sign(H(x))达到了贝叶斯最优错误率,换言之,若指数损失函数最小化。则分类错误率也将最小化;这说明指数损失函数是分类任务原本0/1损失函数的一致的替代损失函数。由于这个替代函数有更好的数学性质,例如他是连续可微函数,因此我们用它代替0/1损失函数。作为优化目标。
在AdaBoost算法中,第一个基分类器 h 1 h_1 h1是通过直接将基学习算法用于初始数据分布而得;此后迭代地生成 h t h_t ht和 a t a_t at,当基分类器 h t h_t ht基于分布 D t D_t Dt产生后,该基分类器的权重 a t a_t at应使得 a t h t a_th_t atht最小化指数损失函数。
ℓ exp ( a t h t ∣ D t ) = E x ∼ D t [ e − f ( x ) a t h t ( x ) ] = e − a t ( 1 − ϵ t ) + e a t ϵ t \ell_{\exp}(a_th_t|D_t)=\mathbb{E}_{x\thicksim D_t}[e^{-f(x)a_th_t(x)}]\\ =e^{-a_t}(1-\epsilon_t)+e^{a_t}\epsilon_t ℓexp(atht∣Dt)=Ex∼Dt[e−f(x)atht(x)]=e−at(1−ϵt)+eatϵt
其中 ϵ t = P x ∼ D t ( h t ( x ) ≠ f ( x ) ) . \epsilon_t=P_{x\thicksim D_t}(h_t(x)\neq f(x)). ϵt=Px∼Dt(ht(x)=f(x)).考虑指数损失函数的导数
∂ ℓ exp ( a t h t ∣ D t ) ∂ a t = − e − a t ( 1 − ϵ T ) + e a t ϵ t \frac{\partial\ell_{\exp}(a_th_t|D_t)}{\partial a_t}=-e^{-a_t}(1-\epsilon_T)+e^{a_t}\epsilon_t ∂at∂ℓexp(atht∣Dt)=−e−at(1−ϵT)+eatϵt
令其为零可得
a t = 1 2 l n ( 1 − ϵ t ϵ t ) a_t=\frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t}) at=21ln(ϵt1−ϵt)
这恰是算法图中第六行的分类器权重更新公式。
AdaBoost算法在获得 H t − 1 H_{t-1} Ht−1之后样本分布将进行调整,使下一轮的基学习器 h t h_t ht能纠正 H t − 1 H_{t-1} Ht−1的一些错误.理想的 h t h_t ht能纠正 H t − 1 H_{t-1} Ht−1的全部错误,即最小化 ℓ exp ( H t − 1 + h t ∣ D ) = E x ∼ D t [ e − f ( x ) ( H t − 1 ( x ) + h t ( x ) ) ] = E x ∼ D t [ e − f ( x ) H t − 1 ( x ) e − f ( x ) h t ( x ) ] \ell_{\exp}(H_{t-1}+h_t|D)=\mathbb{E}_{x\thicksim D_t}[e^{-f(x)(H_{t-1}(x)+h_t(x))}]\\=\mathbb{E}_{x\thicksim D_t}[e^{-f(x)H_{t-1}(x)}e^{-f(x)h_t(x)}] ℓexp(Ht−1+ht∣D)=Ex∼Dt[e−f(x)(Ht−1(x)+ht(x))]=Ex∼Dt[e−f(x)Ht−1(x)e−f(x)ht(x)]
注意到 f 2 ( x ) = h t 2 ( x ) = 1 f^2(x)=h_t^2(x)=1 f2(x)=ht2(x)=1上式可用 e − f ( x ) h t ( x ) e^{-f(x)h_t(x)} e−f(x)ht(x)的泰勒展开近似为
ℓ exp ( H t − 1 + h t ∣ D ) = E x ∼ D t [ e − f ( x ) H t − 1 ( x ) ( 1 − f ( x ) h t ( x ) + f 2 ( x ) h t 2 ( x ) 2 ) ] = E x ∼ D t [ e − f ( x ) H t − 1 ( x ) ( 1 − f ( x ) h t ( x ) + 1 2 ) ] \ell_{\exp}(H_{t-1}+h_t|D)\\=\mathbb{E}_{x\thicksim D_t}[e^{-f(x)H_{t-1}(x)}(1-f(x)h_t(x)+\frac{f^2(x)h_t^2(x)}{2})]\\ =\mathbb{E}_{x\thicksim D_t}[e^{-f(x)H_{t-1}(x)}(1-f(x)h_t(x)+\frac{1}{2})] ℓexp(Ht−1+ht∣D)=Ex∼Dt[e−f(x)Ht−1(x)(1−f(x)ht(x)+2f2(x)ht2(x))]=Ex∼Dt[e−f(x)Ht−1(x)(1−f(x)ht(x)+21)]
于是,理想的基学习器
h t ( x ) = arg max h ℓ exp ( H t − 1 + h ∣ D ) = arg min h E x ∼ D [ e − f ( x ) H t − 1 ( x ) ( 1 − f ( x ) h ( x ) + 1 2 ) ] = arg max h E x ∼ D [ e − f ( x ) H t − 1 ( x ) f ( x ) h ( x ) ] = arg max h E x ∼ D [ e − f ( x ) H t − 1 ( x ) E x ∼ D [ e − f ( x ) H t − 1 ( x ) ] f ( x ) h ( x ) ] h_t(x)=\argmax_h\ell_{\exp}(H_{t-1}+h|D)\\ =\argmin_h\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}(1-f(x)h(x)+\frac{1}{2})]\\ =\argmax_h\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}f(x)h(x)]\\ =\argmax_h\mathbb{E}_{x\thicksim D}[\frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}]}f(x)h(x)] ht(x)=hargmaxℓexp(Ht−1+h∣D)=hargminEx∼D[e−f(x)Ht−1(x)(1−f(x)h(x)+21)]=hargmaxEx∼D[e−f(x)Ht−1(x)f(x)h(x)]=hargmaxEx∼D[Ex∼D[e−f(x)Ht−1(x)]e−f(x)Ht−1(x)f(x)h(x)]
注意到 E x ∼ D [ e − f ( x ) H t − 1 ( x ) ] \mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}] Ex∼D[e−f(x)Ht−1(x)]是一个常数。令 D t D_t Dt表示一个分布
D t ( x ) = D ( x ) e − f ( x ) H t − 1 ( x ) E x ∼ D [ e − f ( x ) H t − 1 ( x ) ] D_t(x)=\frac{D(x)e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}]} Dt(x)=Ex∼D[e−f(x)Ht−1(x)]D(x)e−f(x)Ht−1(x)则根据数学期望的定义这等价于令
h t ( x ) = arg max h E x ∼ D [ e − f ( x ) H t − 1 ( x ) E x ∼ D [ e − f ( x ) H t − 1 ( x ) ] f ( x ) h ( x ) ] = arg max h E x ∼ D [ f ( x ) h ( x ) ] h_t(x)=\argmax_h\mathbb{E}_{x\thicksim D}[\frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}]}f(x)h(x)]\\ =\argmax_h\mathbb{E}_{x\thicksim D}[f(x)h(x)] ht(x)=hargmaxEx∼D[Ex∼D[e−f(x)Ht−1(x)]e−f(x)Ht−1(x)f(x)h(x)]=hargmaxEx∼D[f(x)h(x)]
由 f ( x ) , h ( x ) ∈ { − 1 , + 1 } f(x),h(x)\in\{-1,+1\} f(x),h(x)∈{−1,+1},有
f ( x ) h ( x ) = 1 − 2 ∏ ( f ( x ) ≠ h ( x ) ) f(x)h(x)=1-2∏(f(x)\neq h(x)) f(x)h(x)=1−2∏(f(x)=h(x))
则理想的学习器
h t ( x ) = arg max h E x ∼ D [ ∏ ( f ( x ) ≠ h ( x ) ] h_t(x)=\argmax_h\mathbb{E}_{x\thicksim D}[∏(f(x)\neq h(x)] ht(x)=hargmaxEx∼D[∏(f(x)=h(x)]
由此可见,理想的 h t h_t ht将在分布 D t D_t Dt下最小化分类误差。因此弱分类器将基于分布 D t D_t Dt来训练,且针对 D t D_t Dt的分类误差应小于0.5,这在一定程度上类似“残差逼近”的思想。考虑到 D t D_t Dt和 D t + 1 D_{t+1} Dt+1的关系有
D t + 1 = D ( x ) e − f ( x ) H t ( x ) E x ∼ D [ e − f ( x ) H t ( x ) ] = D ( x ) e − f ( x ) H t − 1 ( x ) e − f ( x ) a t h t ( x ) E x ∼ D [ e − f ( x ) H t ( x ) ] = D t ( x ) e − f ( x ) a t h t ( x ) E x ∼ D [ e − f ( x ) H t − 1 ( x ) ] E x ∼ D [ e − f ( x ) H t ( x ) ] D_{t+1}=\frac{D(x)e^{-f(x)H_{t}(x)}}{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t}(x)}]}\\ =\frac{D(x)e^{-f(x)H_{t-1}(x)}e^{-f(x)a_th_t(x)}}{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t}(x)}]}\\ =D_t(x)e^{-f(x)a_th_t(x)}\frac{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t-1}(x)}]}{\mathbb{E}_{x\thicksim D}[e^{-f(x)H_{t}(x)}]} Dt+1=Ex∼D[e−f(x)Ht(x)]D(x)e−f(x)Ht(x)=Ex∼D[e−f(x)Ht(x)]D(x)e−f(x)Ht−1(x)e−f(x)atht(x)=Dt(x)e−f(x)atht(x)Ex∼D[e−f(x)Ht(x)]Ex∼D[e−f(x)Ht−1(x)]
这恰是图中算法第七行的样本分布更新公式。
于是,我们从基于加性模型迭代式优化指数损失函数的角度推导出了AdaBoost算法。
8.3Bagging与随机森林
欲得到泛化性能强的集成,集成中的个体学习器尽可能相互独立。对给定的数据集,我们可以通过采样产生不同的子集,再从每个子集中训练出一个基学习器。但是,如果每个子集完全不同,相当于每个基学习器只用到了一小部分训练数据,就不能产生好的学习器,为了解决这个问题,我们可考虑使用相互有交叠的采样子集
8.3.1Bagging
Bagging基于自助采样法,给定包含m个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样,经过m次随机采样操作,我们得到含有m个样本的采样集,初始训练集中有的样本在采样集中多次出现,有的则从未出现。这样初始训练集中约有63.2%的样本出现在采样集中。
照这样,我们可以采样出T个含m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合,这就是Bagging的基本流程。在对预测输出进行结合时,Bagging通常对分类任务使用简单投票法,对回归任务使用简单平均法,若分类分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者。
Bagging的算法描述如图所示。
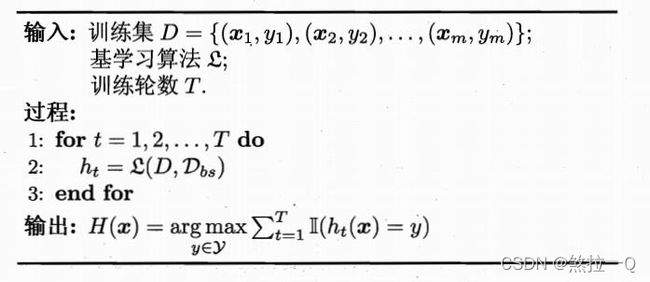
自助采样过程还给Bagging带来了另外一个优点:由于每个基学习器只使用了初始训练集中约63.2%的样本,剩下约36.8%的样本可用作验证集来对泛化性能进行“包外估计”。为此需记录每个基学习器所使用的训练样本。不妨定 D t D_t Dt表示 h t h_t ht实际使用的训练样本集,令 H o o b ( x ) H^{oob}(x) Hoob(x)表示对样本x的包外预测,即仅考虑那些未使用 x x x训练的基学习器在 x x x上的预测。有
H o o b ( x ) = arg max y ∈ Y H^{oob}(x)=\argmax_{y\in Y} Hoob(x)=y∈Yargmax
8.3.2 随机森林
随机森林(Random Forest)是Bagging的一个扩展变体,在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了属性的随机选择。假设样本包含个属性对基决策树的每个节点,先从该节点的属性结合中随机选择包含k( k ≤ d k≤d k≤d)个属性的子集用来进行最优划分。随机森林训练效率通常优于Bagging,因为每个节点的划分只需要部分属性参与,而随机森林的泛化误差通常低于bagging,因为属性的扰动为每个基决策树提供了更高的鲁棒性(不易过拟合到训练集上)。
8.4多样性增强
1.数据样本扰动
对输入扰动敏感的基学习器:决策树、神经网络等
对输入扰动不敏感的基学习器:线性学习器、支持向量机、朴素贝叶斯、k近邻等
2.输入属性扰动
对包含有大量冗余属性的数据能够大幅加速训练效率
3.输出属性扰动
随机改变一些训练样本的标记
Dropout
4.算法参数扰动
L1、L2
正则化等
以上内容源于周志华《机器学习》(西瓜书),笔者以自己的理解写了这篇笔记,如有错误欢迎指正