【C语言】递归讲解

前言
函数递归讲解，递归实例，函数递归与迭代

---

一、什么是递归？

我来告诉你什么是递归！

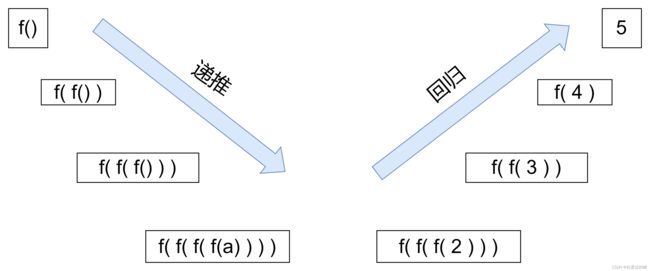
递归就好像你去看病，首先你要去挂号，然后拿着挂号单去找医生，医生了解你的情况后，让你去拍个片。你拿着医生的说明去找拍片，然后你拿着结果去找医生，医生再给你开药，你到药房抓药，最后缴费。到此为止，完成了整个流程，而你也达到了目的。挂号，找医生，拍片这可以看作函数里的自我调用，即“递”，而拿着片找医生，抓药，缴费可以看作“归”。

写成式子是这样的 b=f( f( f( f(a) ) ) ) ，要想求b的值就要先求f( f ( f(a) ) ),先求 f ( f(a) )，先求 f(a)，当我们求出f(a),就要回归求f( f(a) )…,直到求出f( f( f( f(a) ) ) )
假设f(a)=a+1,令a=1

用代码来表示

void function(int a){
 a=1;
 a+=1;
if(a<5)
   function(a);
}

二、递归的要素

2.1子问题

递归实际上就是将一个大问题逐步化解为多个小型、更简单或更具基本性的子问题，这些子问题与原问题在形式上是相同的或类似的，再逐个解决这些个子问题以此来解决原问题。这是我们首先需要考虑的，一个问题是否能用递归来解决。
比如阶乘，10的阶乘不好算，那我们可以先算9的阶乘，8的阶乘，一步步缩小问题，直到1的阶乘。当我们可以把一个大的复杂的问题分成若干个相似的小问题，我们就可以考虑是否用递归来解决问题。

2.2递归调用的结束

我们使用函数递归，每调用一次就会开辟一个栈，栈空间是有限的。所以我们需要一个结束的条件，当不再满足条件，就会跳出来，开始回归。

2.3问题规模的减小（案例：汉诺塔）

在递归过程中，问题的规模必须不断减小，使得每次递归调用都处理一个更小的子问题。否则，递归将永远不会结束。

案例
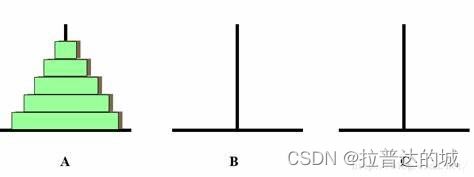
汉诺塔游戏

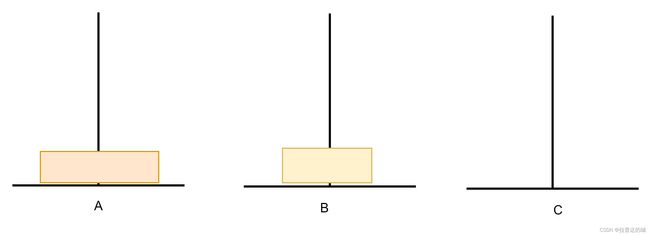
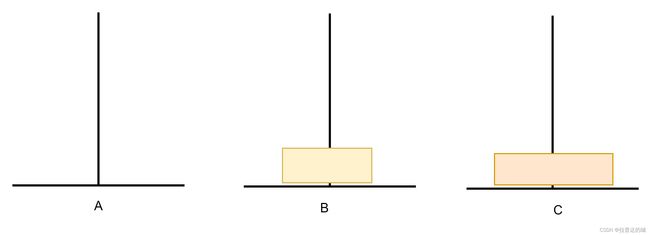
这个游戏就是将A处的五个圆盘挪到C（按从小到大的顺序），且在移动的过程中小的圆盘总是在大圆盘上，一次只能挪一个
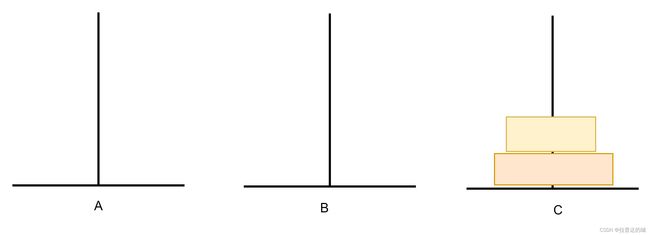
如下，是将三个圆盘挪到C处，且挪动步数是最优解

汉诺塔游戏就是典型的将一个复杂的问题分解成多个小型、更简单或更具基本性的子问题。

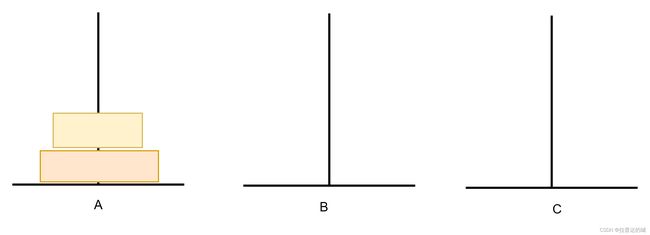
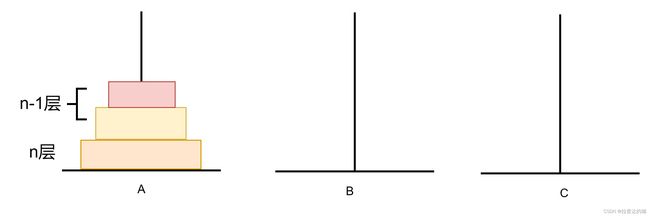
有两层圆盘，我们进行如下三个步骤。那么这就是当我们有n层时，解决n层的子问题

那我们有n层那又该如何解决，我们不妨将n层看作两层，n-1单独作为一层，然后重复两层的操作。

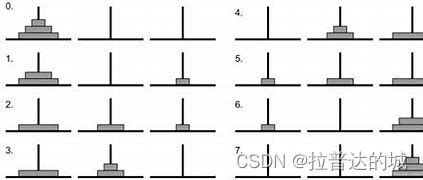
如图，我们将0～3看作步骤一，将4看作步骤二，那么5~7就是步骤三
在0～3我们是不是又可以分为三个步骤，同样5~7也是

如果还是不理解，可以看看B站李永乐老师的
有趣的汉诺塔游戏怎么玩？把大象放冰箱里一共分几步？

2.4汉诺塔游戏的实现

相信汉诺塔游戏的原理都懂了，接着我们用代码来实现

首先写下主函数,接着我们定义变量pos1，pos2，pos3，它们分别表示起始，中转和目的位置。A，B，C并不是和pos1，pos2，pos3绑定在一起的。

int main() {
	char pos1 = 'A';//起始位置
	char pos2 = 'B';//中转位置
	char pos3 = 'C';//目的位置
	int tier = 0;
	scanf("%d",&tier);
	Hanoi(tier,'A','B','C');
	return 0;
}

其中中转位置是什么意思呢？我们要想将n-1层挪到B，肯定要借助C，显而易见，A是n-1层的起始，C是中转，B是目的。这就是我为什么说A，B，C并不是和pos1，pos2，pos3绑定在一起的。

函数Hanoi

void Hanoi(int t,char p1,char p2,char p3) {	
	
	//只有一层的情况
	if (t == 1)
		printf(" %c->%c ", p1, p3);
	else
	{
	    //步骤一
		Hanoi(t - 1, p1, p3, p2);

        //步骤二
		printf(" %c->%c ", p1, p3);
        
        //步骤三
		Hanoi(t - 1, p2, p1, p3);
	}
}

运行结果

三、递归的特点

3.1递归的优点

• 简洁：递归可以将复杂的问题转化为相对简单的子问题，使代码更加简洁和易于理解。通过递归的思想，可以大大降低代码的复杂度，使程序结构更加清晰。

• 直观：递归代码通常能够更加直观地表达问题的本质，因为递归是从问题的定义和解决方法出发进行编程，符合人们对问题的认知。

• 可读性：递归使代码更接近问题本身的描述，使得代码更易于理解和阅读，从而降低了代码的维护难度。

• 分而治之：递归使得复杂的问题可以分解为多个更简单的子问题，这符合“分而治之”（Divide and Conquer）的算法思想，使得问题的解决更加高效。

• 适用于某些问题：有些问题天然适合用递归解决，如树形结构问题、回溯算法、深度优先搜索等。在这些情况下，递归往往是最自然和最直观的解决方案。

3.2递归的缺点

递归的缺点很明显，就是栈溢出。一个问题太复杂，太深，难免会调用很多次函数导致栈溢出。
一个经典案例就是青蛙跳台阶问题

说一个青蛙跳台阶，一次可以跳一阶或者两阶，如果有n阶台阶，那有多少种跳法？
假若有一阶台阶，那只有一种跳法，两阶台阶，有两种跳法，三阶台阶跳法就是一阶台阶的跳法加上两阶台阶的跳法，为什么会这样？实际上，三阶分为最后一次跳的一阶和两阶两种情况，一阶台阶再跳两阶就是三阶台阶，同样两阶台阶再跳一阶也是三阶。因此我们得到一个规律，n阶台阶跳法=（n-1）阶+（n-2）阶。

代码如下

//青蛙跳台阶问题
int JumpSteps(int n) {
		if (n == 1||n == 0)//当只有一阶或零阶楼梯，只有一种跳法或不跳
			return 1;
		else

			//（n-1）和（n-2）分别为最后一步跳了一阶和两阶两种情况，那么跳n阶台阶方法个数就是这两种情况之和
			return JumpSteps(n-1) + JumpSteps(n-2);
	}


int main(){
	int num = 0;
	scanf("%d",&num);
	int count= JumpSteps(num);
	printf("%d",count);
	return 0;
}

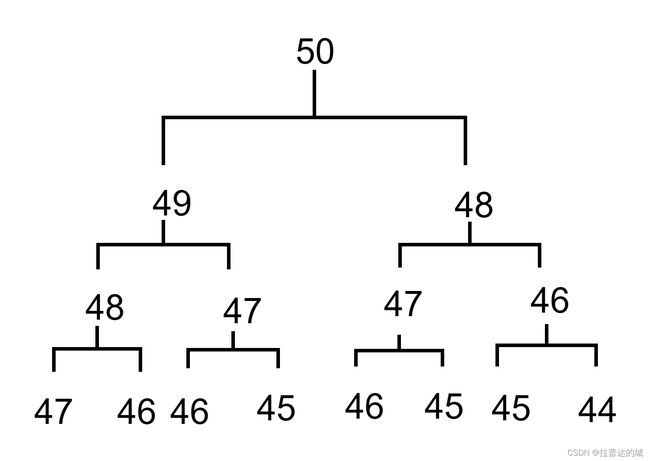
当我们输入50，程序一直执行，不断调用函数，直到n=1或n=0停止，难以想象，函数就像无丝分裂一样，到底会调用多少次，而且调用过程中还有重复的。这样的代码效率低下，不推荐使用递归

3.3递归与迭代

迭代：

• 迭代是一种通过循环来重复执行代码块的方法，通过不断更新循环变量来逐步求解问题。
• 迭代通常需要显式地定义循环变量、循环条件和循环体，使得代码结构更加明确，有助于优化性能。
• 迭代的缺点是可能需要编写较多的代码来实现循环，有时可能不如递归来表达问题的本质。

青蛙跳台阶可以用迭代代替递归

虽然迭代比递归代码长，不够简洁，而且创建了多个变量，但迭代比递归效率高很多

代码如下

#include 

int JumpSteps(int n) {
    if (n == 0 || n == 1) {
        return 1; // 当只有一阶或零阶台阶，只有一种跳法或不跳
    }

    int prev1 = 1; // n-1 阶台阶的跳法数
    int prev2 = 1; // n-2 阶台阶的跳法数
    int current = 0; // 当前台阶的跳法数

    for (int i = 2; i <= n; i++) {
        current = prev1 + prev2;
        prev2 = prev1;
        prev1 = current;
    }

    return current;
}

int main() {
    int num;
    printf("请输入台阶数 n：");
    scanf("%d", &num);

    int count = JumpSteps(num);
    printf("%d 阶台阶的跳法数为 %d\n", num, count);
    return 0;
}

四、总结

选择递归还是迭代，取决于问题的性质、规模和实现的方便程度。所以不管是迭代还是递归，总归给我们提供了不同的思路，当我们遇到问题时，不妨尝试思考，哪种方法效率更高，实现更加容易。
有时，递归和迭代可以互相转换。在递归解决的问题中，有些可以通过迭代的方式来实现，而在一些迭代解决的问题中，也可以通过递归的方式来解决。选择哪种方法，要看具体的问题和编程的要求。

---

如果你喜欢这篇文章，点赞+评论+关注⭐️哦！
欢迎大家提出疑问，以及不同的见解。