LeetCode 63. 不同路径 II
63. 不同路径 II
题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
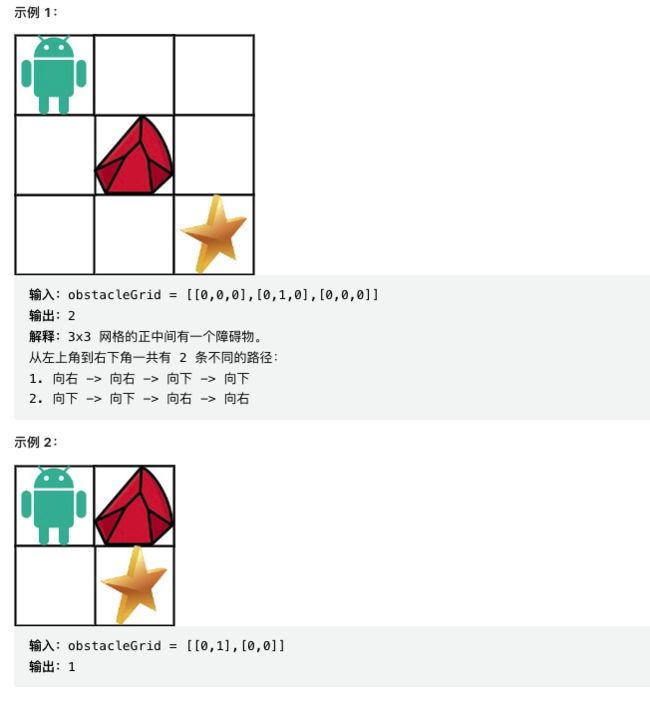
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
解题思路
思路一: 动态规划
1. 状态定义
dp[i][j] 表示走到格子 (i, j)(i,j) 的方法数
2. 状态转移
如果网格 (i, j) 上有障碍物,则 dp[i][j] 值为 0,表示走到该格子的方法数为 0;
否则网格 (i, j) 可以从网格 (i - 1, j)或者 网格 (i, j - 1) 走过来,因此走到该格子的方法数为走到网格 (i - 1, j) 和网格 (i, j - 1) 的方法数之和,即 dp[i, j] = dp[i - 1, j] + dp[i, j - 1]。
状态转移方程如下:
d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] , ( i , j ) 上无障碍物 0 , ( i , j ) 上有障碍物 dp[i][j] = \begin{cases} dp[i - 1][j] + dp[i][j - 1], &(i, j)上无障碍物\\ 0, &(i, j)上有障碍物 \end{cases} dp[i][j]={dp[i−1][j]+dp[i][j−1],0,(i,j)上无障碍物(i,j)上有障碍物
3. 初始条件
初始化二维数组,初始化值都为0
第 1 列的格子只有从其上边格子走过去这一种走法,因此初始化 dp[i][0] 值为 1,存在障碍物时为 0;
第 1 行的格子只有从其左边格子走过去这一种走法,因此初始化 dp[0][j] 值为 1,存在障碍物时为 0。
注意: 初始化数组的时候, 要考虑 上一个状态,如果有一个为障碍物,以后的 值都要是 0 , 而不是只考虑当前 是否为障碍物的情况, 而是当前如果为障碍物了, 以后所有的值都为0 代表不可达。
4. 遍历顺序
由状态转移方程知道dp[i] 是从 dp[i−1,j] 和 dp[i,j−1] 转移过来所以从前往后遍历
5. 返回值
返回dp[m - 1][n - 1]
实现代码如下:
/**
* @param {number[][]} obstacleGrid
* @return {number}
*/
var uniquePathsWithObstacles = function(obstacleGrid) {
let m = obstacleGrid.length,
n = obstacleGrid[0].length;
dp = Array.from(Array(m), () => Array(n).fill(0));
//初始化注意
for(let i = 0;i < m;i++) {
if(obstacleGrid[i][0] == 1){ // 如果出现障碍物,则该行之后的都不可到达
break;
}
dp[i][0] = 1;
}
for(let j = 0;j < n;j++) {
if(obstacleGrid[0][j] == 1){
break;
}
dp[0][j] = 1;
}
for(let i = 1;i < m;i++){
for(let j = 1;j < n;j++){
// 去除障碍物
if(obstacleGrid[i][j] == 1) continue;
if(obstacleGrid[i][j] == 0){
//约束条件
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
};
时间复杂度:O(mn)
空间复杂度:O(mn)
优化版本
dp[i][j] 只与 dp[i - 1][j] 和 dp[i][j - 1] 相关,我们可以运用「滚动数组思想」把空间复杂度优化称 O(m) 。
/**
* @param {number[][]} obstacleGrid
* @return {number}
*/
var uniquePathsWithObstacles = function(obstacleGrid) {
let m = obstacleGrid.length,
n = obstacleGrid[0].length,
dp = Array(n).fill(0);
dp[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
continue;
}
if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
dp[j] += dp[j - 1];
}
}
}
return dp[n - 1];
};
空间复杂度:O(m)
参考资料
https://leetcode.cn/problems/unique-paths-ii/solution/jian-dan-dpbi-xu-miao-dong-by-sweetiee/