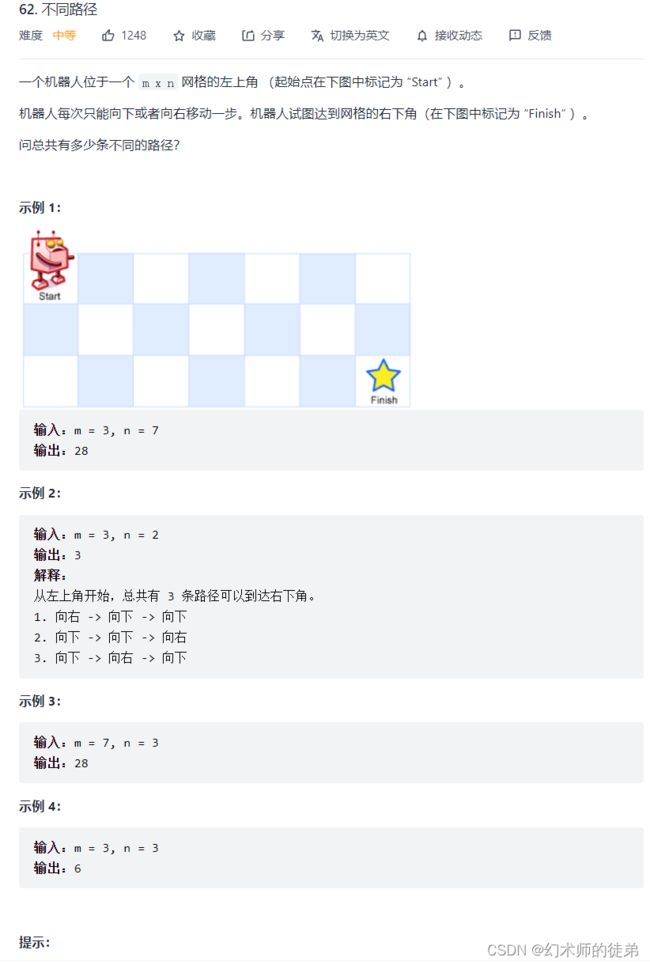
LeetCode62. 不同路径

题目概述

题目链接：点我做题

解法

一、缓存递归法优化

  我们定义$dp[i][j]$为题目在中所说的条件下，一个$i\ast j$矩阵从左上角走到右下角的不同路径个数，那么对于当前位置来说，其实只有两种选择，要么向右走，要么向下走，由于这一步不同，这两个事件是互斥的；
  如果向右走，第一步向右走不就相当于把列数减1，行数不变，数学一点描述这句话，就是一个$m\ast n$矩阵从左上角出发，到达右下角，且第一步向右走到达的不同路径个数，等于一个$i\ast (j-1)$矩阵从左上角走到右下角的不同路径个数；
  同理，如果第一步向下走，就是一个$m\ast n$矩阵从左上角出发，到达右下角，且第一步向下走到达的不同路径个数，等于一个$(i-1)\ast j$矩阵从左上角走到右下角的不同路径个数；
  再思考一些边界条件，当i等于1的时候，那么矩阵退化为了一个行向量，到达右下角走法只有一种：一直向右走；当j等于1的时候，矩阵退化为一个列向量，到达右下角走法同样只有一种：一直向下走。
  状态转移方程如下：
$$\begin{gathered} dp[i][j]=dp[i-1][j]+dp[i][j-1] \\ foralli,dp[i][1]=1; \\ forallj,dp[1][j]=1; \end{gathered}$$
  下面我们用缓存化的思路用递归实现这个题。

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int>> dp(m, vector<int>(n));
        //STL中的元素值，默认初始化为0
        return _uniquePaths(m, n, dp);
    }
    int _uniquePaths(int m, int n, vector<vector<int>>& dp)
    {
        if (dp[m - 1][n - 1] != 0)
        {
            //如果不为0，说明之前计算过了 直接返回
            return dp[m - 1][n - 1];
        }
        int ret = 0;
        if (m == 1 || n == 1)
        {
            //如果m或n减到1了，对应dp[1][j]=1,dp[i][1]=1;
            ret = 1;
        }
        else
        {
            //否则，向下走和向右走加起来
            //由于它们是互斥的，这一步是合法的
            int a = _uniquePaths(m - 1, n, dp);
            int b = _uniquePaths(m, n - 1, dp);
            ret = a + b;
        }
        //缓存储存起来
        dp[m - 1][n - 1] = ret;
        return ret;
    }
};

时间复杂度：$O(m\ast n)$
空间复杂度：$O(m\ast n)$,存储状态m*n的数组，递归由于存储了状态，最多m*n层。

二、直接动态规划

  观察状态转移方程：
$$\begin{gathered} dp[i][j]=d[i-1][j]+dp[i][j-1] \\ foralli,dp[i][1]=1; \\ forallj,dp[1][j]=1; \end{gathered}$$
  发现dp[i][j]的值只和比它下标小的值有关，我们可以通过循环,从小下标计算到大下标，计算$dp[i][j]$,代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int>> dp(m, vector<int>(n));
        for (int i = 0; i < m; i++)
        {
            //初始化dp[i][0]都成1
            dp[i][0] = 1;
        }
        for (int j = 1; j < n; j++)
        {
            //初始化dp[0][j]都成1
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

时间复杂度:$O(m\ast n)$
空间复杂度:$O(m\ast n)$

三、优化版动态规划（主要优化空间复杂度）

  其实前面能直接通过两层循环来以计算过的值来计算$dp[i][j]$还有一个原因，观察我们的状态转移方程：
$$\begin{gathered} dp[i][j]=dp[i-1][j]+dp[i][j-1] \\ foralli,dp[i][1]=1; \\ forallj,dp[1][j]=1; \end{gathered}$$
  如果外层循环遍历i，内层循环遍历j，那么在i固定，j不断加1变化时，dp[i][j]的值只和外层的上一轮遍历得到的dp[i-1][j]的值和在遍历j时，上次计算dp[i][j-1]的值，这些值都计算过，所以这样用二层循环来遍历是合法的。
  从这就可以看出我们优化的地方在哪了，我们只需要一个数组维护上次外层循环遍历(大小为内层遍历的循环次数)的计算值和一个临时变量维护上次内层循环的计算值不就可以了，并且为了记录上次外层遍历的结果的数组空间最小，我们可以如果n>m，那么让0<=j   注意到一个事实$m\ast n$矩阵从左上角到右下角走法的不同路径数和$n\ast m$矩阵从左上角到右下角的不同路径数一样，所以我们可以只写一份i在外面的代码，如果n>m就去交换m和n的值。

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        //优化动态规划
        //观察到dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        //所以两层循环遍历j时，只要保存上一层i的dp和j - 1前置就好
        if (n > m)
        {
            int tmp = m;
            m = n;
            n = tmp;
        }
        vector<int> dp(n, 1);
        for (int i = 1; i < m; i++)
        {
            int prev = dp[0];
            for (int j = 1; j < n; j++)
            {
                dp[j] = dp[j] + prev;
                prev = dp[j];
            }
        }
        return dp.back();
    }
};

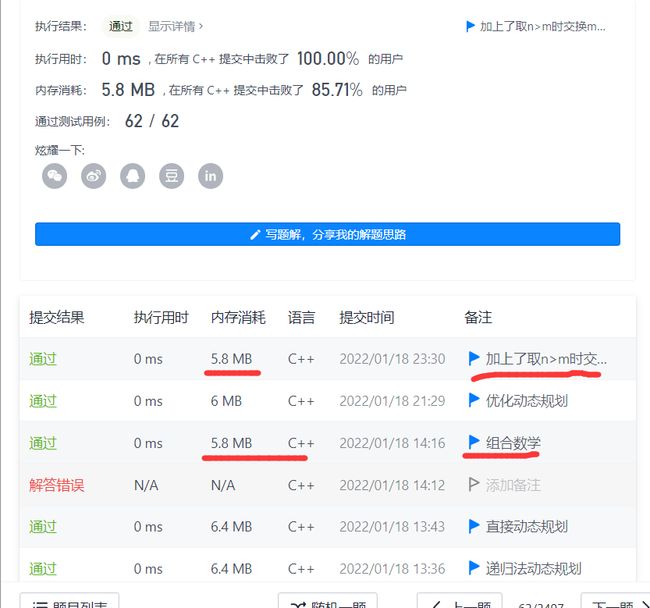
  下面这图也可以看出来这波优化的空间复杂度确实降低了很多，内存消耗和我们下面要讲的组合数学方法(空间复杂度O(1))都差不多了。

时间复杂度：$O(m\ast n)$
空间复杂度：$O(min(m,n))$

四、排列组合法

  思考一下，如果只能向下走或者向右走，那么从$m\ast n$矩阵的左上角到达右下角的总步数一定是$m+n-2$，向右走的步数一定是$m-1$步，向下走的步数一定是$n-1$步，每一步选择向下走或是向右走会导致完全不同的走法，所以我们总的走法数目等于从$m+n-2$步中选出$m-1$步向下走，那么剩下的步骤就是向右走，由于每一步向下或向右都不同，选法有$C_{m+n-2}^{m-1}$种，根据数学公式，这个组合数等于：
$$C_{m+n-2}^{m-1}=\frac{(m+n-2)!}{(m-1)!(n-1)!}=\frac{(m-2+n)\ast (m-3+n)...\ast n}{(m-1)!}$$
  如果语言内置了阶乘，直接用就好，C++没内置，我们用循环模拟一下：

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        //排列组合法
        //发现从左上角走到右下角总共要走m + n - 2步
        //其中要走m - 1步向右走 n - 1步向下走
        //选第一步向下走和选第二部向下走是完全不同的
        //所以我们要从m + n - 2步里选出m - 1步向右走
        //这时 剩下的步骤一定是向下走 就选完了
        long long ret = 1;
        //控制m一定比n小，那么这个循环次数就可以最少
        if (m > n)
        {
            int tmp = m;
            m = n;
            n = tmp;
        }
        for (int i = 1; i <= m - 1; i++)
        {
            ret = ret * (n + i - 1) / i;
        }
        return ret;
    }
};

时间复杂度:$O(min(m,n))$
空间复杂度：$O(1)$