【计算机组成原理】一文搞懂原码、反码、补码和位运算符（左移右移按位与异或等）

1.什么是源码补码反码

1. 机器数
   一个数在计算机中的表示形式是二进制的话，这个数其实就叫机器数。

机器数通常是带有符号的（指有正数和负数之分），计算机用最高位存放符号，这个 bit 一般叫做符号位。 正数的符号位为 0， 负数的符号位为 1。比如，十进制中的数 +7 ，计算机字长为8位，转换成二进制就是 0 0 0 0 0 1 1 1（一个 byte 有 8bit，有效的取值范围是 -128 ~ +127）。

如果是 -7 ，就是 1 0 0 0 0 1 1 1 。一个存储的二进制码分原码、反码、补码，下面我们就来介绍一下什么是原码、反码、补码
补充：
计算机底层使用二进制形式的补码来计算和存储数据

1.原码

十进制数据的二进制表现形式就是原码，原码最左边的一个数字就是符号位，0为正，1为负。

例如：56 -> 0 0 1 1 1 0 0 0

左边第一位为符号位，其他位为数据位。

一个 byte 有 8bit，最大值是 0 1 1 1 1 1 1 1 (+127)，最小值是 1 1 1 1 1 1 1 1 (-128)

在计算机中之所以使用二进制来表示原码是因为逻辑简单，对于电路来说只有开或者关两种状态，用二进制是在方便不过的了。如果使用的进制是十进制、八进制或者十六进制的话，电路没有办法表示那么多的状态

正数计算
使用原码对正数进行计算不会有任何问题的

例如：5 + 2

 0 0 0 0 0 1 0 1
+        0 0 1 0
-----------------
 0 0 0 0 0 1 1 1

把这个结果转成十进制刚好就等于 7，完全正确无误

负数计算
但是如果是负数的话，那计算的结果就会大相径庭了

我们拿 -56 这个数字来举例，它的原码是 1 0 1 1 1 0 0 0 ，减一之后，就会变成 1 0 1 1 0 1 1 1 ，这个数转成十进制就是 -55。计算前是 -56，减一之后正确的结果应该是 -57（1 0 1 1 1 0 0 1）才对，居然还越减越大了

 1 0 1 1 1 0 0 0
-              1
-----------------
 1 0 1 1 0 1 1 1

为了解决原码不能用于计算负数的这种问题，这时候，反码它出现了，作为负数的“计算的救星”。

计算规则是正数的反码不变和原码一致，负数的反码会在原码的基础上，高位的符号位不变，其他位取反（ 1 变成 0 ， 0 变为 1 ）。

2.反码

正数的反码是其本身（等于原码），负数的反码是符号位保持不变，其余位取反。 反码的存在是为了正确计算负数，因为原码不能用于计算负数

负数计算
这时候，我们再来使用反码计算一下 -56 - 1 的结果

-56 的原码是 1 0 1 1 1 0 0 0 ，如果转成反码（符号位不变，其他位取反），

那么它的反码就是 1 1 0 0 0 1 1 1

  1 1 0 0 0 1 1 1
 -              1
-----------------
  1 1 0 0 0 1 1 0

-56 -1 = -57，-57 的原码是 1 0 1 1 1 0 0 1，转成反码刚好是 1 1 0 0 0 1 1 0，刚好等于刚才我们算出的值

跨零计算
不过反码也有它的 “ 软肋 ”，如果是负数跨零进行计算的话，计算得出的结果不对

我们拿 -3 + 5 来举例

-3 的原码是 1 0 0 0 0 0 1 1，转成反码的话就是 1 1 1 1 1 1 0 0

 1 1 1 1 1 1 0 0
+        0 1 0 1  
-----------------
 0 0 0 0 0 0 0 1 

把计算结果转成十进制就是 1，这结果显然不对。那么我们该怎么计算呢，这时候，作为反码的补充编码 —— 补码就出现了。

3.补码

正数的补码是其本身，负数的补码等于其反码 +1。因为反码不能解决负数跨零（类似于 -6 + 7）的问题，所以补码出现了。

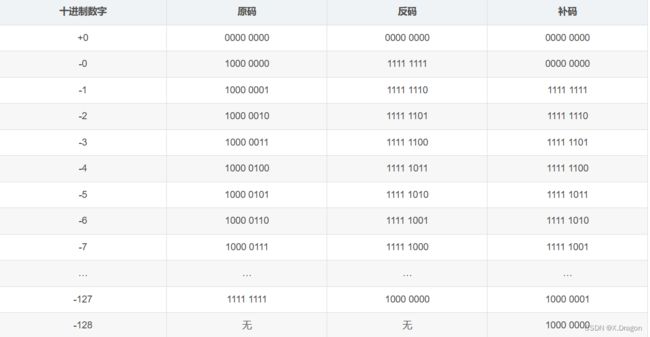
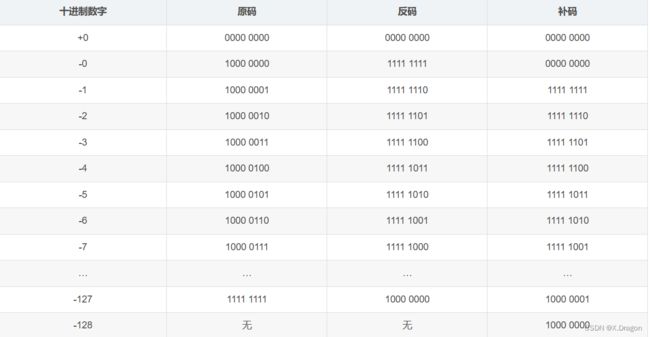- 跨零计算
这时候，我们再来使用反码计算一下 -3 + 5 的结果

-3 的原码是 1 0 0 0 0 0 1 1，转成反码的话就是 1 1 1 1 1 1 0 0，再转成补码就是 1 1 1 1 1 1 0 1

 1 1 1 1 1 1 0 1
+        0 1 0 1
----------------- 
 0 0 0 0 0 0 1 0

把这个数转成十进制刚好等于2，结果正确

4、总结

在计算机当中都是使用补码来进行计算和存储的。补码很好的解决了反码负数不能跨零计算的弊端，并且补码还可以记录一个特殊的值 -128，这个数据在 1 个字节下是没有原码和反码

学习了原码、反码和补码的知识之后，我们就可以了解到，Java 当中所有的基本数据类型。比如整数类型的数据类型，存储的数都是同样的，区别是在于什么地方，假设存储的值都是 10

2. 位操作

一、前言

在C语言中除了算数操作符、关系操作符、逻辑操作符外还有一类操作符 “ 位操作符 ”。这类操作符可以直接对内存中存储的二进制位进行操作，但有个前提条件：其所操作的对象只能是整形家族的成员（char、short、int、long、longlong）。为什么呢？拿浮点型举个例子吧。你看啊，我们都知道整形与浮点型在内存中的存储方式是完全不同的，如果胡乱的按照处理整形数据时的观念操作浮点数，那必然乱套啊。所以说到底位操作符就是专门为操作整数而存在的，下面就来介绍一下吧。

二、整数在内存中的存储形式

在讲位操作符之前我们先需要了解一下整数在内存中的存储形式才行。我们都知道一个整数在内存中需要4个字节的空间来存放，也就是32个二进制位。而这32个二进制位对于有符号整数来说最高位为符号位（为0则表示正数，为1则表示负数），所以有符号整数表示的范围在：-2,147,483,648 ~ 2,147,483,647；而对于无符号整数来说最高位并不是符号位，因为其本来就是用来表示非负整数的，所以表示范围在：0 ~ 4,294,967,295。值得补充的一点是：在32个二进制位中我们通常把最右边的那位称为最高位，最坐边的那位称为最低位。
  整数有三种表示形式：原码、反码、补码。但值得注意的是：整数最终在内存中是以补码的形式存放的。并不是有些参考资料上说的：正整数是以原码的形式存放，负整数是以补码的形式存放。它这么说是为了方便记忆罢了，与真实情况是不符的。所以记住只要是整数，内存中存储的都是二进制的补码，只不过正数的原码、反码、补码相同，而负数的原、反、补不同，补码是要通过一系列计算才能得到。 而对于无符号整数来说，由于其全是正整数所以压根就不存在负数，所以原码、反码、补码和正数一样是相同的。
  要得到负数的补码，首先就要先写出负数的原码（原码按照最高位为符号位来写），不拿写出 -1 的原码为：10000000000000000000000000000001；然后通过原码写出它的反码（原码的符号位不变其他位按位取反得到的就是反码），所以反码为：11111111111111111111111111111110；最后通过反码写出补码（反码加1就是补码），所以补码为：11111111111111111111111111111111 。值得注意的是printf()函数在打印整数时是通过读取内存中的补码，然后将其转换成原码的形式再打印的。简单来说就是printf()函数打印的是这个数的原码，记住了。

三、位操作符

C语言中基本的位操作符有： 左移、右移、按位与、按位或、按位异或、取反。警告：对于移位操作，不要移动负数位，这个是标准未定义的！！！

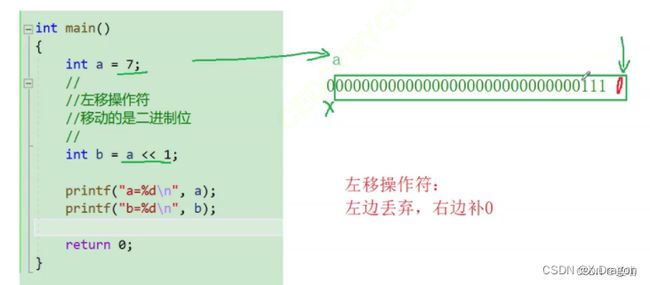
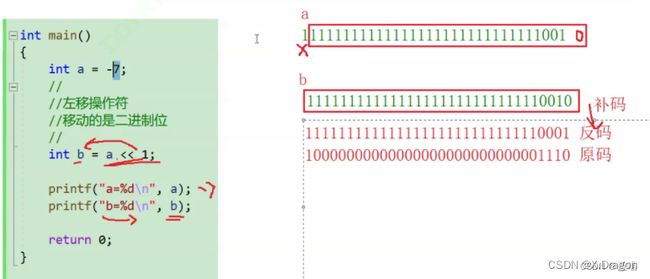
3.1 左移"<<"
  左移是双目运算符 “ << ” ，运算符左边是移动对象，右边是左移位数（整形表达式）。左移时高位丢弃，低位补0。如下图所示的，正整数7向左移动一位后不难算出结果为14；负整数-7向左移动一位结果为-14。

3.2 右移">>"
  右移运算符的使用方法与左移一样，不同的是移位方向相反。而且右移分为两种：算数右移、逻辑右移。算数右移：低位丢弃，高位补原符号位。逻辑右移：低位丢弃，高位补0。而在vs编译器中采用的是算数右移，如下图所示：

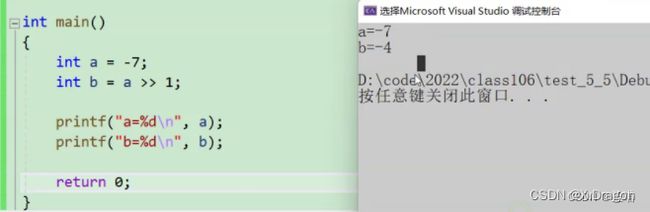
经过一段时间后你一定会惊讶的发现，左移操作符向左移动一位相当于乘上一个2 ^ 1，左移两位就相当于乘上一个2 ^ 2。而右移操作符右移一位相当于除上一个2 ^ 1。

3.3 按位取反"~"
  按位取反是位运算符中唯一的一个单目运算符，运算符为 “ ~ ” 。其功能是：把目标的二进制位按位取反，即：使得每一位上的0变成1，1变成0。例子如下：

3.4 按位与"&"
  运算符 “ & ” 的作用是：把参见运算两个数所对应的二进制位分别进行“与”运算，即：两位同为“1”，结果才为“1”，否则为0。例子如下：

3.5 按位或"|"
  运算符 “ | ” 的作用是：把参见运算两个数所对应的二进制位分别进行“或”运算，即：两位同为“0”，结果才为“0”，否则为1。例子如下：

3.6 按位异或"^"
  按位异或运算规则为：把参见运算两个数所对应的二进制位分别进行“异或”运算，相同为0，相异为1。例子如下：

四、总结

通过上面的讲解相信大家已经对位操作符有所了解了，但大家有没有想过其实位操作符的对象可以是char、short、int、long、longlong型的，而这些类型的二进制位数是不同的，那该如何进行运算呢？遇到这种情况，系统会自动进行处理对齐操作，被称为：隐式类型的转换。

拓展阅读： 链接: 算法 | 如何用位运算实现加减运算？