初识GAN

前言

　　简单认识下GAN，GAN与最大似然的关系，几个基本概念的介绍

GAN

对抗网络

　　GAN的思想，一个判别模型D，一个生成模型G组成对抗网络。如何对抗呢？ D的目的是尽量识别出G生成的样本， D(x) 表示样本被判断为真实数据的概率；G的目的是尽量让D无法识别自己生成的样本。
　　生成对抗网络的D之优化函数：

V(G,D)=Ex∼pdata[lnD(x)]+Ex∼pg[ln(1−D(x))]

　　这个优化函数是怎么来的呢？ 本质是最大似然参数估计。

最大似然参数估计

　　先来回顾下最大似然估计问题，以二分类为例。
　　样本总是唯一地属于某个类1/0，假设正样本标记为1，负样本标记为0。
　　在一个样本在label已知时，则样本为类别y=label的概率为：

P(y|x;θ)=[P(y=1|x;θ)]T[y=1]∗[1−P(y=1|x;θ)]T[y=0]

　　其中 T[⋅] 表示判断是否为真，真则=1，假则=0。样本类别具有唯一性，故T[Y]也表示了随机变量 Y 发生的概率(Import)，发生时概率为1，不发生时概率为0，这个特点将交叉熵和最大似然完美统一起来（对这里要解释地没用可以忽略）。
　　最大似然估计参数的思想是：选择某参数θ ，使得，当前样本集出现的总体概率 L(D;θ)=P(Y|D;θ) 最大，即：

maxθ{P(Y|D;θ)}=maxθ{∏imP(yi|xi;θ)}

==>等价于max{Ln[L(D;θ)]}=max{∑imlnP(yi|xi;θ)}

∝max{1m∑imlnP(yi|xi;θ)}≈Ex∼p真实分布[lnP(yi|xi;θ)]

　　最后一步：对某随机变量而言，其总体期望可以用样本的均值估计。

V(G,D) 与ML 关系

　　对抗网络的样本来自真实数据 xi 和生成数据 G(zi) ，天然分裂为label=1（当 xi∈data 时）和label=0（当 xi∈G(zi) 时），判别器判别某样本类型y=label的概率函数可以表示为 P(y|x;(θd)) ，生成器的模型表示为 G(z) ，其中 z 为随机噪声。
　　其样本集判别为各自类别的总概率：

∏im[D(xi;θd)]T[y=1][1−D(G(zi;θg))]T[y=0]

=∏imD(xi;θd)T[xi∈data][1−D(xi;θd)]T[xi∈G(zi)]

==>等价于∑x∈datalnP(y|x;θd)+∑x∈G(z)[1−lnP(y|x;θd)]

∝1m1∑x∈datalnP(y|x;θd)+1m2∑x∈G(x)[1−lnP(y|x;θd)]

≈Ex∼pdata[lnP(y|x;θd)]+Ex∼pg(z)[1−lnP(y|x;θd)]

　　再变化下形式

=Ex∼pdata[lnD(x)]+Ex∼pg(x)[1−D(x)]

=Ex∼pdata[lnD(x)]+Ez∼Pg(z)[1−D(G(z))]

=Ex∼pdata[lnD(x)]+Ex∼Pg(x)[1−D(G(x))]

　　到这里就清晰了，对抗网络的判别器D的优化函数与ML是一致的，都是最大化当前样本集的出现总概率（判对的总概率），用样本均值估计全体均值。

生成器的优化目标

　　对抗网络，还有另一方生成器 G(z;θg) 。它的优化目标是什么呢？
　　G对自身参数的优化方向，依赖于外部，主要是让D对其生成样本无法识别，最好是判断概率为0.5。

maxθg{1−D(G(z;θg))}

对抗学习过程

　　前面只是介绍了对抗网络的组成结构，及优化目标的构造，怎么具体训练呢？

学习过程

　　需要注意的是，G和D的训练时交叉进行的。

为什么有效

　　两个最优+一个过程收敛。
　　1) given G ， 则D∗G(x)=Pdata(x)Pdata(x)+Pg(x)。
　　如何解释： V(G,D) 化简
　　　　 =∫xpdata(x)lnD(x)dx+∫zpz(z)ln(1−D(G(z)))dz
　　　　 =∫xpdata(x)lnD(x)dx+∫xpg(x)ln(1−D(x))dx
　　　　 =∫xalny+bln(1−y)dx
　　最后的式子在 y=aa+b 时，取得最值。有空再想这个最值求解吧。

　　2) given D∗ ，则 V(G,D∗) 在 Pg=Pd 时，有最值 V∗(G,D∗)=−ln4 。
　　在 D∗ 下，整体的最优状态是什么样子呢？预期是 pg=pd ，且 D(G(z))=12 。验证下是否是呢？
　　 V(G,D∗) 化简：
　　　　 =Ex∼pdata[lnPdata(x)Pdata(x)+Pg(x)]+Ex∼pg[lnPg(x)Pdata(x)+Pg(x)]
　　　　 =∑x∈datapd(x)lnlnPd(x)Pd(x)+Pg(x)+∑x∈G(z)Pg(x)lnlnPg(x)Pd(x)+Pg(x)
　　　　 =∑x∈datapd(x)ln2lnPd(x)Pd(x)+Pg(x)+∑x∈G(z)Pg(x)ln2lnPd(x)Pd(x)+Pg(x)
　　　　 −∑x∈dataPd(x)ln2−∑x∈GPg(x)ln2=−1∗ln2−1∗ln2=−ln4
　　　　 =KL(Pd||Pd+Pg2)+KL(Pg||Pd+Pg2)−ln4
　　对于最后的式子，可以根据KL最值得知， Pd=Pd+Pg2; Pg=Pd+Pg2时，有最小值KL=0 ，从而得证 V(G,D∗) 的最优值及条件。
　　
　　3) 训练过程收敛。
　　训练过程是交叉进行的，分别优化G和D， opt{G|givenD∗t}⇔opt{D|givenG∗} 。实际训练过程不容易收敛到最优值，进一步优化看GCGAN。GAN的论文有个Table2对生成模型面临的难点总结了下。

优缺点

　　优点：
　　1） 训练时，只需要BackPropagation和dropout即可，不需要使用MC（Markov Chain），不需要根据网络推断某些分布。Import
　　2）对抗网络，对任意可导函数有效。
　　3）生成模型不用直接根据真实样本更新，而是利用流经判别模型的梯度。减少了数据依赖。
　　4）生成模型可表示的分布 Pg 更多样化，可以表示陡峭的分布，而MC训练的分布对此力不从心。Import
　　缺点：
　　1） Pg 表示方式不明确。
　　2）G和D的训练要同步好，否则容易G(x)生成单一性太强的样本，无法训练。

思考

　　两方对抗，多方对抗有没有可能？纳什均衡、博弈论的内容看下。

名词解释

　　1) momentum
　　梯度下降的加速技巧：积累之前的同向梯度，震荡方向的梯度相互抵消。
　　将参数更新 θt+1=θt−ηΔtJ(θ) 替换为：

{vt+1=γvt+ηΔtJ(θ)θt+1=θt−vt+1，其中γ<1,general=0.9

　　更常规的moment版本如下：

{vt+1=βvt+(1−β)ΔtJ(θ)θt+1=θt−ηvt+1

　　为避免初始值过低，做bias-correcte如下： v=v1−βt ，推导过程可以将 v 表示为加和形式，然后尝试E[v] 正相关于 E[dw] ，就会发现为什么这么除分母项。
　　 2) dropout algorithm
　　 解决问题：针对DeepNet训练overfit的问题，而提出的一种类似RandomForest的bagging思想的方法。
　　 如何dropout：每次训练时，对输入节点按照0.2的概率drop，对隐藏节点按照0.5的概率drop。
　　drop的意思是这个节点在本次不起作用，包括forward的计算和backward的误差后传。
　　 辅助regular：与dropout相应的辅助调参技巧： Max-nrom regularization。
　　对任意隐藏节点 hi ，在更新参数后，限制其最大squared-nrom值<=L。 Wi,j 表示隐藏节点 hi 的输入侧权重向量。
　　

{Whi,j=Whi,jWhi,j=Whi,jLL′,if ∑jWhi,j=L′<=L,others
　　 3) ReLU和Leak ReLU
　　激活函数的一种类型，具有更好的特性： 更具生物特性；导数常值不消失等。
　　基本函数形式： ReLU(x)=max(0,x)={0x,if x≤0,others
　　使用形式 ReLU(x)=max(0,wx+b) ，其梯度 Grad={0w,if wx+b≤0,others
　　ReLU比sigmoid要好使的讨论： https://www.zhihu.com/question/29021768

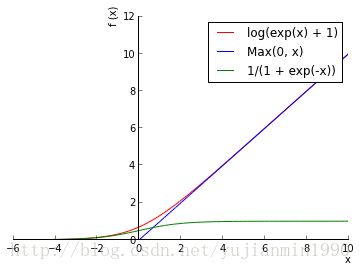
　　可以用pych实现下不同active function，试试。
　　ReLU的变种： Leaky ReLU(x)={λxx,if x≤0,others 。其中 λ∈(0,1)
　　4) batch normalization
　　 解决问题：网络的每层输入都要受到上层的参数变化而导致输入数据的分布变化，被称作“internal covariate shift”。
　　batch-normalizing transform。
　　对某一节点 y=g(wx+b) 变为 y=g[BN(wx+b)]
　　 i.e.

　　对每个输入维度 xi 都有对应的 yi=γkxi^+βk 。
　　其中梯度如下：

　　据作者说，BN可以丢掉对dropout的依赖。同时，可以毫无障碍地使用larger learning rate（max-norm也是可以用更大的学习率）。可以降低对L2的依赖。等好处…
　　5) maxout
　　6) global average pooling
　　7) trided convolution

参考

　　1) https://ishmaelbelghazi.github.io/ALI/
　　2) http://blog.aylien.com/introduction-generative-adversarial-networks-code-tensorflow/
　　3)《Generative Adversarial Nets》
　　4)《Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks》
　　5) 《Batch Normalization, Accelerating Deep Network Training by Reducing Internal Covariate Shift》
　　6）《Dropout, A Simple Way to Prevent Neural Networks from Overfitting》