CEC2018:动态多目标测试函数DF10~DF14的PS及PF(提供Matlab代码)
现实世界中,许多优化问题不仅具有多属性,而且与时间相关,即随着时间的变化,优化问题本身也发生改变,这类问题称为动态多目标优化问题(dynamic multi-objective optimization problems,DMOP)。DMOP是一类目标之间相互冲突,目标函数、约束函数和相关参数等可能随着时间的变化而改变的多目标优化问题。不失一般性,以最小化多目标问题为研究对象,一个具有n个决策变量,m个目标函数的DMOP可以描述为:
{ min x ∈ Ω ( x , t ) = ( f 1 ( x , t ) , f 2 ( x , t ) , ⋯ , f m ( x , t ) ) T s ⋅ t ⋅ g i ( x , t ) ⩽ 0 ( i = 1 , 2 , ⋯ , p ) h j ( x , t ) = 0 ( j = 1 , 2 , ⋯ , q ) \left\{\begin{array}{l} \min _{x \in \Omega}(\boldsymbol{x}, t)=\left(f_{1}(\boldsymbol{x}, t), f_{2}(\boldsymbol{x}, t), \cdots, f_{m}(\boldsymbol{x}, t)\right)^{T} \\ s \cdot t \cdot g_{i}(\boldsymbol{x}, t) \leqslant 0(i=1,2, \cdots, p) \\ h_{j}(\boldsymbol{x}, t)=0(j=1,2, \cdots, q) \end{array}\right. ⎩ ⎨ ⎧minx∈Ω(x,t)=(f1(x,t),f2(x,t),⋯,fm(x,t))Ts⋅t⋅gi(x,t)⩽0(i=1,2,⋯,p)hj(x,t)=0(j=1,2,⋯,q)
其中 , t 为时间变量 , x = ( x 1 , x 1 , ⋯ , x n ) ∈ Ω 为 n 维决策变量 , F = ( f 1 , f 2 , ⋯ , , f m ) 为 m 维目标向量 , g i ⩽ 0 ( i = 1 , 2 , ⋯ , p ) 为 p 个不等式约束 , h j = 0 ( j = 0 , 1 , ⋯ , q ) 为 q 个等式约束。 其中, t 为时间变量, \\x=\left(x_{1}, x_{1}, \cdots, x_{n}\right) \in \Omega 为 n 维决策变量, \\\boldsymbol{F}=\left(f_{1}, f_{2}, \cdots,\right. , \left.f_{m}\right) 为 m 维目标向量, \\ g_{i} \leqslant 0(i=1,2, \cdots, p) 为 p 个不等式约束,\\ h_{j}=0(j=0 , 1, \cdots, q) 为 q 个等式约束。 其中,t为时间变量,x=(x1,x1,⋯,xn)∈Ω为n维决策变量,F=(f1,f2,⋯,,fm)为m维目标向量,gi⩽0(i=1,2,⋯,p)为p个不等式约束,hj=0(j=0,1,⋯,q)为q个等式约束。
一、CEC2018简介
CEC2018共有14个测试函数:DF1-DF14,其中DF1-DF9是两个目标,DF10-DF14是三个目标。
![]()
二、测试函数
点击查看DF1-DF5详细信息
点击查看DF6-DF9详细信息
点击查看DF10-DF14详细信息
%% 画PS
figure
for i=1:maxgen/taut
plot(h(i).dataPS(:,1),h(i).dataPS(:,2),'.')
hold on;
end
% grid on;
xlabel('\it\fontname{Times New Roman}x_1'); ylabel('\it\fontname{Times New Roman}x_2');
title(strcat(probID,'-PS'))
%% 画PF
figure
if TestProblem<10
if (TestProblem==1)||(TestProblem==2)||(TestProblem==3)||(TestProblem==6)
for i=1:maxgen/taut
plot(h(i).dataPF(:,1),h(i).dataPF(:,2),'.')
hold on;
end
xlabel('\it\fontname{Times New Roman}f_1'); ylabel('\it\fontname{Times New Roman}f_2');
elseif (TestProblem==4)||(TestProblem==5)||(TestProblem==7)||(TestProblem==9)
for i=1:maxgen/taut
plot(h(i).dataPF(:,1)+2*h(i).t,h(i).dataPF(:,2)+2*h(i).t,'.')
hold on;
end
xlabel('\it\fontname{Times New Roman}f_1+2t'); ylabel('\it\fontname{Times New Roman}f_2+2t');
else
for i=1:maxgen/taut
plot(h(i).dataPF(:,1)+4*h(i).t,h(i).dataPF(:,2)+4*h(i).t,'.')
hold on;
end
xlabel('\it\fontname{Times New Roman}f_1+4t'); ylabel('\it\fontname{Times New Roman}f_2+4t');
end
else
for i=1:maxgen/taut
plot3(h(i).dataPF(:,1),h(i).dataPF(:,2),h(i).dataPF(:,3),'.')
hold on;
end
xlabel('\it\fontname{Times New Roman}f_1'); ylabel('\it\fontname{Times New Roman}f_2');zlabel('\it\fontname{Times New Roman}f_3');
end
% grid on;
title(strcat(probID,'-PF'))
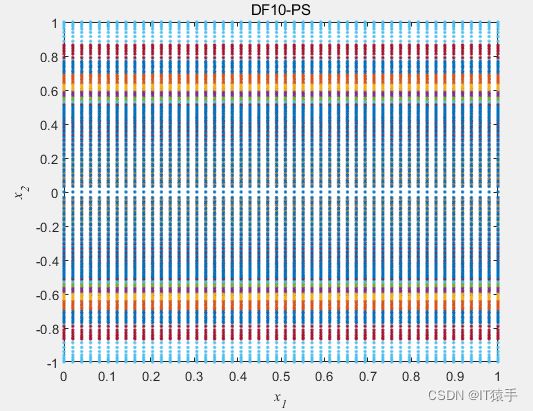
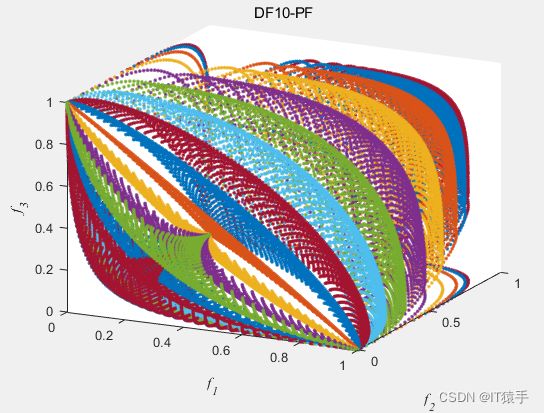
2.10 DF10:PS随时间变化,PF随时间变化
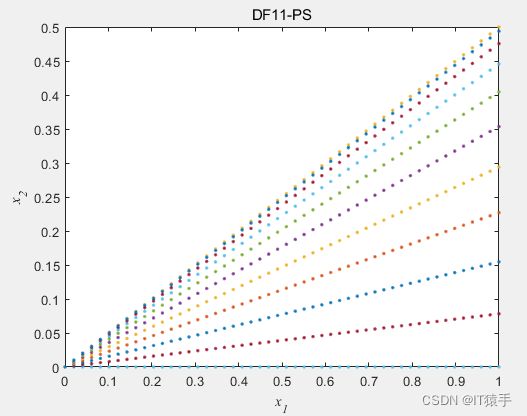
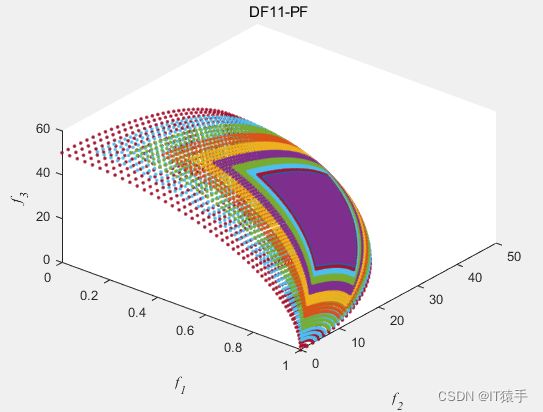
2.11 DF11:PS随时间变化,PF随时间变化
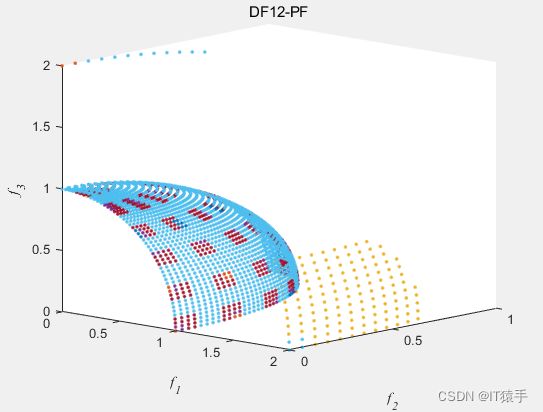
2.12 DF12:PS随时间变化,PF随时间变化
2.13 DF13:PS随时间变化,PF随时间变化
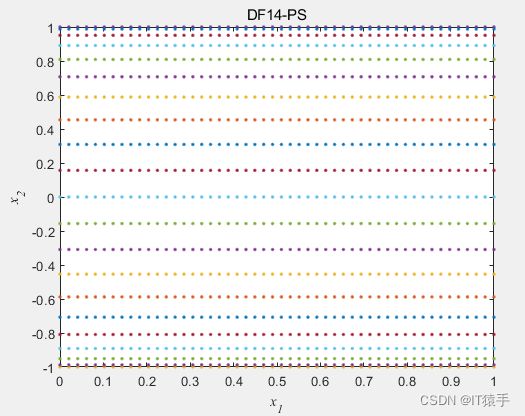
2.14 DF14:PS随时间变化,PF随时间变化
三、完整代码
文件夹内包含动态多目标测试函数DF6、DF7、DF8和DF9的PS及PF完整MATLAB代码。