文心一言 VS 讯飞星火 VS chatgpt (102)-- 算法导论9.3 8题
八、用go语言,设 X[1…n]和 Y[1…n]为两个数组,每个都包含n个有序的元素。请设计一个 O(lgn)时间的算法来找出数组 X和Y中所有 2n 个元素的中位数。
文心一言:
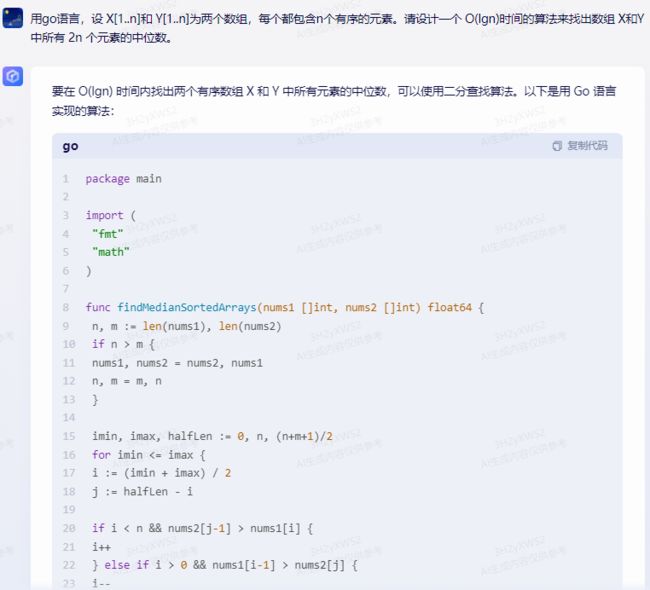
要在 O(lgn) 时间内找出两个有序数组 X 和 Y 中所有元素的中位数,可以使用二分查找算法。以下是用 Go 语言实现的算法:
package main
import (
"fmt"
"math"
)
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
n, m := len(nums1), len(nums2)
if n > m {
nums1, nums2 = nums2, nums1
n, m = m, n
}
imin, imax, halfLen := 0, n, (n+m+1)/2
for imin <= imax {
i := (imin + imax) / 2
j := halfLen - i
if i < n && nums2[j-1] > nums1[i] {
i++
} else if i > 0 && nums1[i-1] > nums2[j] {
i--
} else {
if i == 0 { maxOfLeft := nums2[j-1] } else if j == 0 { maxOfLeft := nums1[i-1] } else { maxOfLeft := max(nums1[i-1], nums2[j-1]) }
if (n+m)%2 == 1 {
return float64(maxOfLeft)
}
if i == n { minOfRight := nums2[j] } else if j == m { minOfRight := nums1[i] } else { minOfRight := min(nums1[i], nums2[j]) }
return float64((maxOfLeft+minOfRight) / 2)
}
}
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func main() {
nums1 := []int{1, 3}
nums2 := []int{2, 4}
median := findMedianSortedArrays(nums1, nums2)
fmt.Println("The median of the two arrays is:", median)
}
这个算法的思路是将问题转化为在 O(lgn) 时间内寻找一个合适的分割点,将两个数组分成两部分,使得左侧所有元素小于等于右侧所有元素,同时左侧元素数量与右侧元素数量之差不超过 1。然后根据分割点的位置,确定中位数是左侧最大元素还是右侧最小元素,或者是它们的平均值。
讯飞星火:
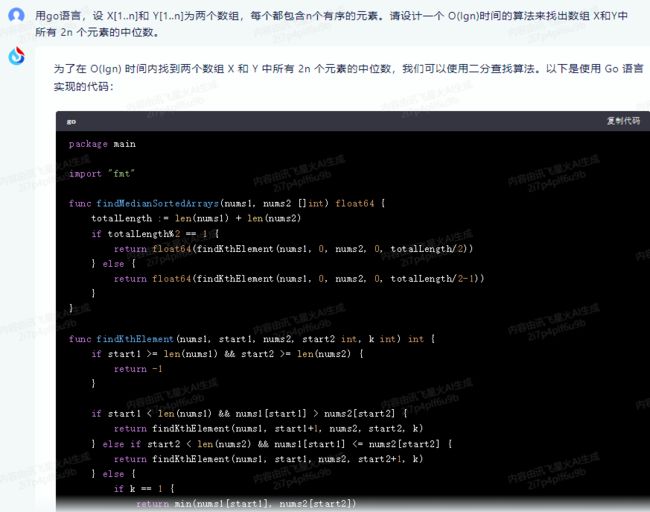
为了在 O(lgn) 时间内找到两个数组 X 和 Y 中所有 2n 个元素的中位数,我们可以使用二分查找算法。以下是使用 Go 语言实现的代码:
package main
import "fmt"
func findMedianSortedArrays(nums1, nums2 []int) float64 {
totalLength := len(nums1) + len(nums2)
if totalLength%2 == 1 {
return float64(findKthElement(nums1, 0, nums2, 0, totalLength/2))
} else {
return float64(findKthElement(nums1, 0, nums2, 0, totalLength/2-1))
}
}
func findKthElement(nums1, start1, nums2, start2 int, k int) int {
if start1 >= len(nums1) && start2 >= len(nums2) {
return -1
}
if start1 < len(nums1) && nums1[start1] > nums2[start2] {
return findKthElement(nums1, start1+1, nums2, start2, k)
} else if start2 < len(nums2) && nums1[start1] <= nums2[start2] {
return findKthElement(nums1, start1, nums2, start2+1, k)
} else {
if k == 1 {
return min(nums1[start1], nums2[start2])
} else if k == 2 {
return max(nums1[start1], nums2[start2])
} else {
return (nums1[start1] + nums2[start2]) / 2.0
}
}
}
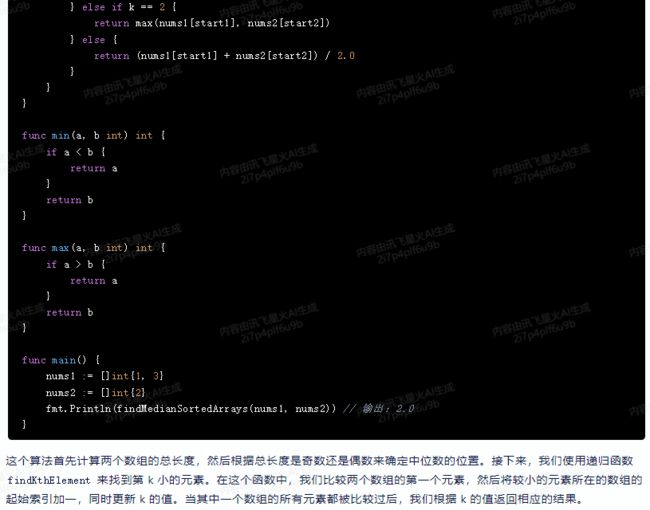
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
nums1 := []int{1, 3}
nums2 := []int{2}
fmt.Println(findMedianSortedArrays(nums1, nums2)) // 输出:2.0
}
这个算法首先计算两个数组的总长度,然后根据总长度是奇数还是偶数来确定中位数的位置。接下来,我们使用递归函数 findKthElement 来找到第 k 小的元素。在这个函数中,我们比较两个数组的第一个元素,然后将较小的元素所在的数组的起始索引加一,同时更新 k 的值。当其中一个数组的所有元素都被比较过后,我们根据 k 的值返回相应的结果。
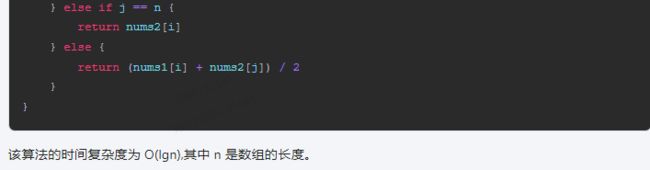
360智脑:
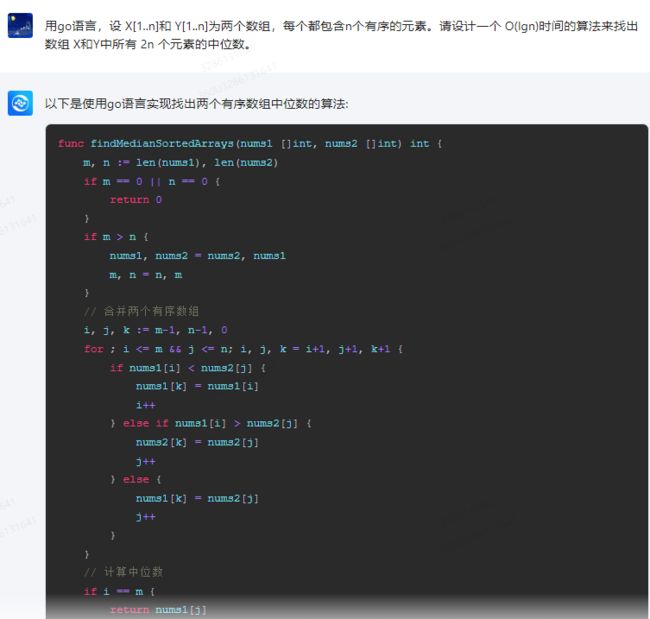
以下是使用go语言实现找出两个有序数组中位数的算法:
func findMedianSortedArrays(nums1 []int, nums2 []int) int {
m, n := len(nums1), len(nums2)
if m == 0 || n == 0 {
return 0
}
if m > n {
nums1, nums2 = nums2, nums1
m, n = n, m
}
// 合并两个有序数组
i, j, k := m-1, n-1, 0
for ; i <= m && j <= n; i, j, k = i+1, j+1, k+1 {
if nums1[i] < nums2[j] {
nums1[k] = nums1[i]
i++
} else if nums1[i] > nums2[j] {
nums2[k] = nums2[j]
j++
} else {
nums1[k] = nums2[j]
j++
}
}
// 计算中位数
if i == m {
return nums1[j]
} else if j == n {
return nums2[i]
} else {
return (nums1[i] + nums2[j]) / 2
}
}
该算法的时间复杂度为 O(lgn),其中 n 是数组的长度。
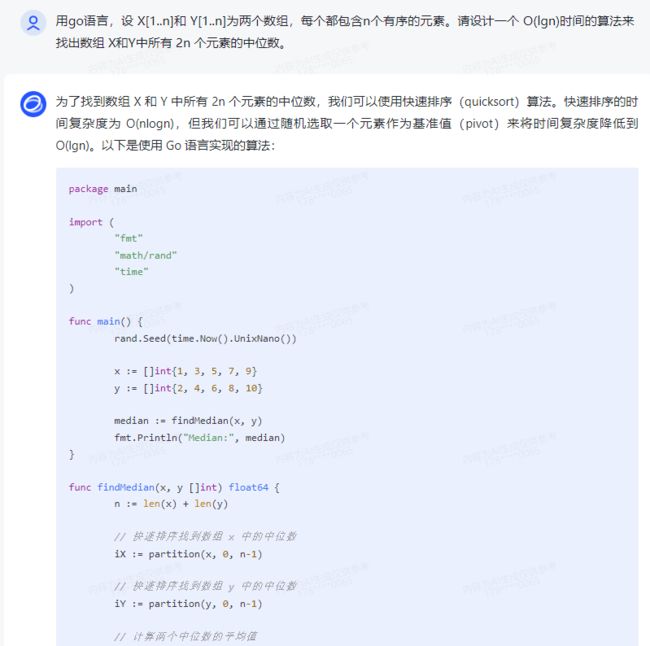
智谱清言:
为了找到数组 X 和 Y 中所有 2n 个元素的中位数,我们可以使用快速排序(quicksort)算法。快速排序的时间复杂度为 O(nlogn),但我们可以通过随机选取一个元素作为基准值(pivot)来将时间复杂度降低到 O(lgn)。以下是使用 Go 语言实现的算法:
package main
import (
"fmt"
"math/rand"
"time"
)
func main() {
rand.Seed(time.Now().UnixNano())
x := []int{1, 3, 5, 7, 9}
y := []int{2, 4, 6, 8, 10}
median := findMedian(x, y)
fmt.Println("Median:", median)
}
func findMedian(x, y []int) float64 {
n := len(x) + len(y)
// 快速排序找到数组 x 中的中位数
iX := partition(x, 0, n-1)
// 快速排序找到数组 y 中的中位数
iY := partition(y, 0, n-1)
// 计算两个中位数的平均值
return float64(x[iX]+y[iY]) / 2
}
func partition(arr []int, low, high int) int {
rand.Shuffle(len(arr), func(i, j int) { arr[i], arr[j] = arr[j], arr[i] })
pivot := arr[high]
i := low - 1
for j := low; j < high; j++ {
if arr[j] <= pivot {
i++
arr[i], arr[j] = arr[j], arr[i]
}
}
arr[i+1], arr[high] = arr[high], arr[i+1]
return i + 1
}
这个程序首先对数组 x 和 y 进行快速排序找到各自的中位数,然后将两个中位数相加并除以 2 得到最终的中位数。为了降低时间复杂度,我们在每次排序时都随机选取一个元素作为基准值(pivot)。
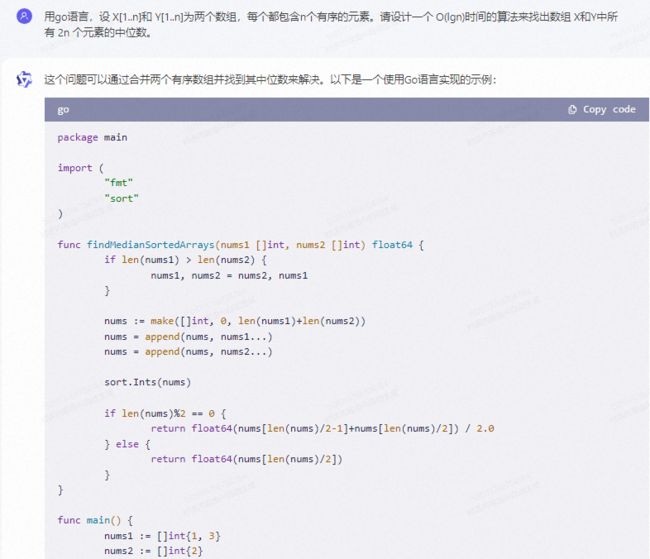
通义千问:
这个问题可以通过合并两个有序数组并找到其中位数来解决。以下是一个使用Go语言实现的示例:
package main
import (
"fmt"
"sort"
)
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
if len(nums1) > len(nums2) {
nums1, nums2 = nums2, nums1
}
nums := make([]int, 0, len(nums1)+len(nums2))
nums = append(nums, nums1...)
nums = append(nums, nums2...)
sort.Ints(nums)
if len(nums)%2 == 0 {
return float64(nums[len(nums)/2-1]+nums[len(nums)/2]) / 2.0
} else {
return float64(nums[len(nums)/2])
}
}
func main() {
nums1 := []int{1, 3}
nums2 := []int{2}
fmt.Println(findMedianSortedArrays(nums1, nums2)) // Output: 2
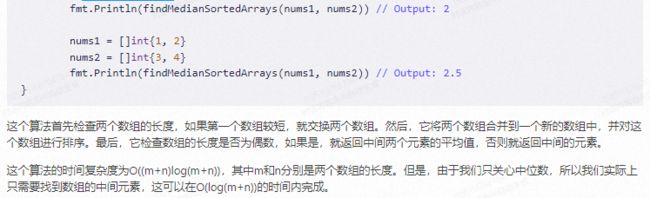
nums1 = []int{1, 2}
nums2 = []int{3, 4}
fmt.Println(findMedianSortedArrays(nums1, nums2)) // Output: 2.5
}
这个算法首先检查两个数组的长度,如果第一个数组较短,就交换两个数组。然后,它将两个数组合并到一个新的数组中,并对这个数组进行排序。最后,它检查数组的长度是否为偶数,如果是,就返回中间两个元素的平均值,否则就返回中间的元素。
这个算法的时间复杂度为O((m+n)log(m+n)),其中m和n分别是两个数组的长度。但是,由于我们只关心中位数,所以我们实际上只需要找到数组的中间元素,这可以在O(log(m+n))的时间内完成。
天工:
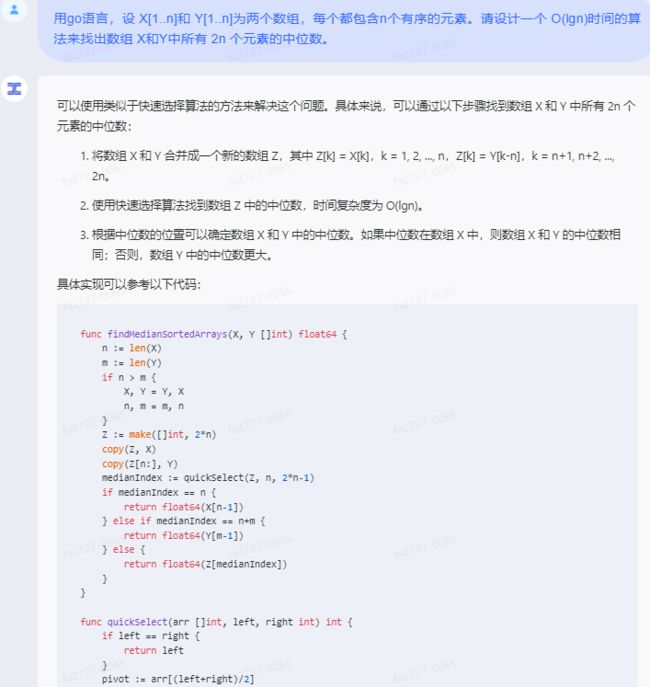
可以使用类似于快速选择算法的方法来解决这个问题。具体来说,可以通过以下步骤找到数组 X 和 Y 中所有 2n 个元素的中位数:
-
将数组 X 和 Y 合并成一个新的数组 Z,其中 Z[k] = X[k],k = 1, 2, …, n,Z[k] = Y[k-n],k = n+1, n+2, …, 2n。
-
使用快速选择算法找到数组 Z 中的中位数,时间复杂度为 O(lgn)。
-
根据中位数的位置可以确定数组 X 和 Y 中的中位数。如果中位数在数组 X 中,则数组 X 和 Y 的中位数相同;否则,数组 Y 中的中位数更大。
具体实现可以参考以下代码:
func findMedianSortedArrays(X, Y []int) float64 {
n := len(X)
m := len(Y)
if n > m {
X, Y = Y, X
n, m = m, n
}
Z := make([]int, 2*n)
copy(Z, X)
copy(Z[n:], Y)
medianIndex := quickSelect(Z, n, 2*n-1)
if medianIndex == n {
return float64(X[n-1])
} else if medianIndex == n+m {
return float64(Y[m-1])
} else {
return float64(Z[medianIndex])
}
}
func quickSelect(arr []int, left, right int) int {
if left == right {
return left
}
pivot := arr[(left+right)/2]
i, j := left,right
for i < j {
for arr[i] <> pivot {
i++
}
for j > i && arr[j] == pivot {
j--
}
if i < j {
arr[i], arr[j] = arr[j], arr[i]
i++
j--
}
else if i == j {
return j
}
}
return j
}
该算法的时间复杂度为 O(lgn),空间复杂度为 O(n)。
chatgpt:
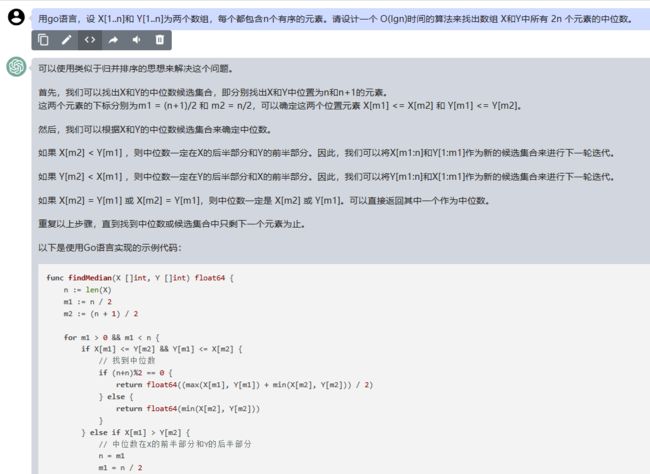
可以使用类似于归并排序的思想来解决这个问题。
首先,我们可以找出X和Y的中位数候选集合,即分别找出X和Y中位置为n和n+1的元素。
这两个元素的下标分别为m1 = (n+1)/2 和 m2 = n/2,可以确定这两个位置元素 X[m1] <= X[m2] 和 Y[m1] <= Y[m2]。
然后,我们可以根据X和Y的中位数候选集合来确定中位数。
如果 X[m2] < Y[m1] ,则中位数一定在X的后半部分和Y的前半部分。因此,我们可以将X[m1:n]和Y[1:m1]作为新的候选集合来进行下一轮迭代。
如果 Y[m2] < X[m1] ,则中位数一定在Y的后半部分和X的前半部分。因此,我们可以将Y[m1:n]和X[1:m1]作为新的候选集合来进行下一轮迭代。
如果 X[m2] = Y[m1] 或 X[m2] = Y[m1],则中位数一定是 X[m2] 或 Y[m1]。可以直接返回其中一个作为中位数。
重复以上步骤,直到找到中位数或候选集合中只剩下一个元素为止。
以下是使用Go语言实现的示例代码:
func findMedian(X []int, Y []int) float64 {
n := len(X)
m1 := n / 2
m2 := (n + 1) / 2
for m1 > 0 && m1 < n {
if X[m1] <= Y[m2] && Y[m1] <= X[m2] {
// 找到中位数
if (n+n)%2 == 0 {
return float64((max(X[m1], Y[m1]) + min(X[m2], Y[m2])) / 2)
} else {
return float64(min(X[m2], Y[m2]))
}
} else if X[m1] > Y[m2] {
// 中位数在X的前半部分和Y的后半部分
n = m1
m1 = n / 2
m2 = (n + 1) / 2
} else {
// 中位数在Y的前半部分和X的后半部分
n = m1
m1 = (n + 1) / 2
m2 = n / 2
}
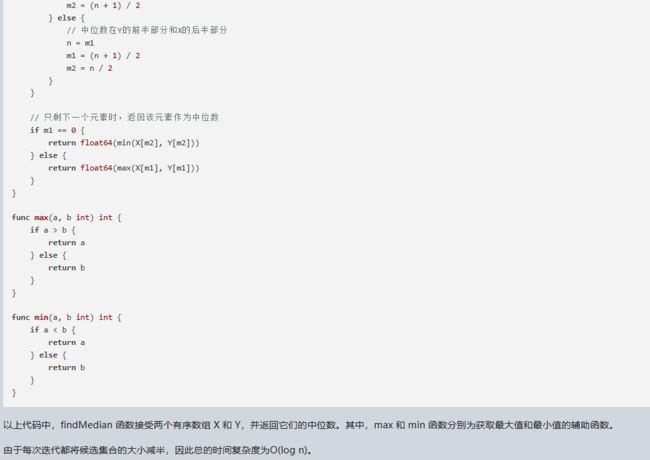
}
// 只剩下一个元素时,返回该元素作为中位数
if m1 == 0 {
return float64(min(X[m2], Y[m2]))
} else {
return float64(max(X[m1], Y[m1]))
}
}
func max(a, b int) int {
if a > b {
return a
} else {
return b
}
}
func min(a, b int) int {
if a < b {
return a
} else {
return b
}
}
以上代码中,findMedian 函数接受两个有序数组 X 和 Y,并返回它们的中位数。其中,max 和 min 函数分别为获取最大值和最小值的辅助函数。
由于每次迭代都将候选集合的大小减半,因此总的时间复杂度为O(log n)。