《论文阅读27》SuperGlue: Learning Feature Matching with Graph Neural Networks
一、论文
- 研究领域: 图像特征点匹配
- 论文:SuperGlue: Learning Feature Matching with Graph Neural Networks
- CVPR 2020
- veido
- 论文code
二、论文简述
[参考] [参考] [参考]
三、论文详述
SuperGlue:使用图神经网络学习特征匹配
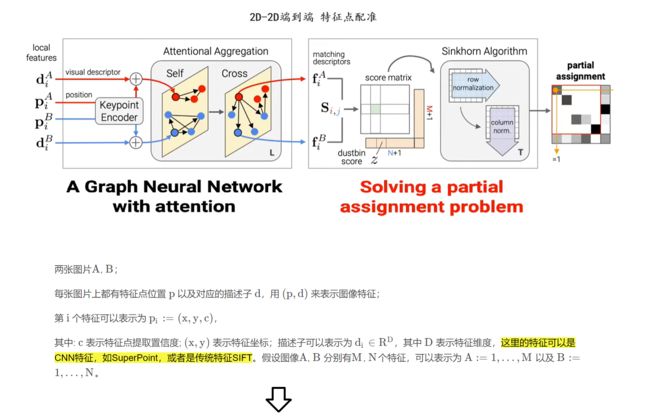
本文介绍了SuperGlue,一种神经网络,通过共同寻找对应点和拒绝不匹配点来匹配两组本地特征。分配估计通过解决一个可微的最优运输问题,其成本预测的图形神经网络。我们引入了一个灵活的上下文聚合机制的基础上的注意力,使SuperGlue的原因有关的基础3D场景和功能分配联合。与传统的手工设计的启发式算法相比,我们的技术通过从图像对进行端到端的训练来学习3D世界的几何变换和规则。SuperGlue优于其他学习方法,并在具有挑战性的真实世界室内和室外环境中的姿态估计任务上取得了最先进的结果。所提出的方法在现代GPU上实时执行匹配,并且可以容易地集成到现代SfM或SLAM系统中
- Introduction
图像中的点之间的对应关系对于在几何计算机视觉任务(诸如同时定位和映射(SLAM)和运动恢复结构(SfM))中估计3D结构和相机姿态是必不可少的。这种对应性通常通过匹配局部特征来估计,这是一种被称为数据关联的过程。大的视点和光照变化、遮挡、模糊和缺乏纹理是使2D到2D数据关联特别具有挑战性的因素。
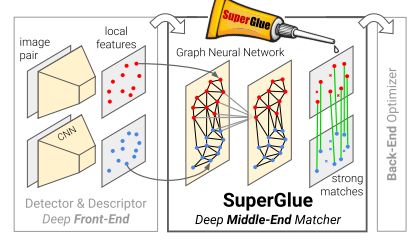
在本文中,我们提出了一种新的思维方式的特征匹配问题。本文提出了一种基于SuperGlue神经网络的局部特征匹配算法,该算法不需要学习任务不可知的局部特征,然后通过简单的匹配启发式算法和技巧来完成匹配过程。在SLAM环境中,通常[8]将问题分解为视觉特征提取前端和束调整或姿势估计后端,我们的网络直接位于中间- SuperGlue是一个可学习的中间端(见图1)。
与SuperGlue的特征匹配。我们的方法从现成的局部特征建立逐点对应:它充当手工或学习的前端和后端之间的中间端。SuperGlue使用图形神经网络和注意力来解决分配优化问题,并优雅地处理部分点的可见性和遮挡,从而产生部分分配。
在本文中,学习特征匹配被视为寻找两组局部特征之间的部分分配。通过求解线性分配问题,我们重新审视了经典的基于图的匹配策略,当将线性分配问题放松为最优运输问题时,可以微分地求解线性分配问题。该优化的成本函数由图神经网络(GNN)预测。受Transformer [61]成功的启发,它使用自我(图像内)和交叉(图像间)注意力来利用关键点的空间关系及其视觉外观。该公式强制执行预测的分配结构,同时使成本能够学习复杂的先验知识,优雅地处理遮挡和不可重复的关键点。我们的方法是从图像对中进行端到端的训练--我们从一个大型的带注释数据集中学习姿势估计的先验知识,使SuperGlue能够推理3D场景和分配。我们的工作可应用于各种需要高质量特征对应的多视图几何问题(见图2)。
图2:SuperGlue对应关系。对于这两个具有挑战性的室内图像对,使用SuperGlue进行匹配可以获得准确的姿势,而其他学习或手工制作的方法则会失败(对应关系被极线误差着色)。
我们展示了SuperGlue与手工制作的匹配器和学习的内点分类器相比的优越性。当与SuperPoint [18](一种深度前端)相结合时,SuperGlue推进了室内和室外姿势估计任务的最新技术,并为端到端深度SLAM铺平了道路。
- Related work
局部特征匹配通常通过以下步骤来执行:
i)检测兴趣点,
i)计算视觉描述符,
iii)将这些与最近邻(NN)搜索进行匹配,
iv)过滤不正确的匹配,
最后v)估计几何变换。
21世纪初开发的经典管道通常基于SIFT [31],过滤器匹配Lowe比率测试[31],相互检查和启发式方法,如邻域共识[59,10,6,49],并使用RANSAC [21,43]等鲁棒求解器找到变换。
最近的深度学习匹配工作通常集中在使用卷积神经网络(CNN)从数据中学习更好的稀疏检测器和局部描述符[18,19,37,45,69]。为了提高它们的区分度,一些作品使用区域特征[32]或对数极坐标补丁[20]明确地查看更广泛的背景。其他方法通过将其分类为内点和离群点来学习过滤匹配[33,44,7,71]。这些操作仍然通过NN搜索估计的匹配集,因此忽略分配结构并丢弃视觉信息。到目前为止,学习执行匹配的作品集中在密集匹配[46]或3D点云[65]上,并且仍然表现出相同的限制。相比之下,我们的可学习的中间端同时执行上下文聚合,匹配和过滤在一个单一的端到端架构。
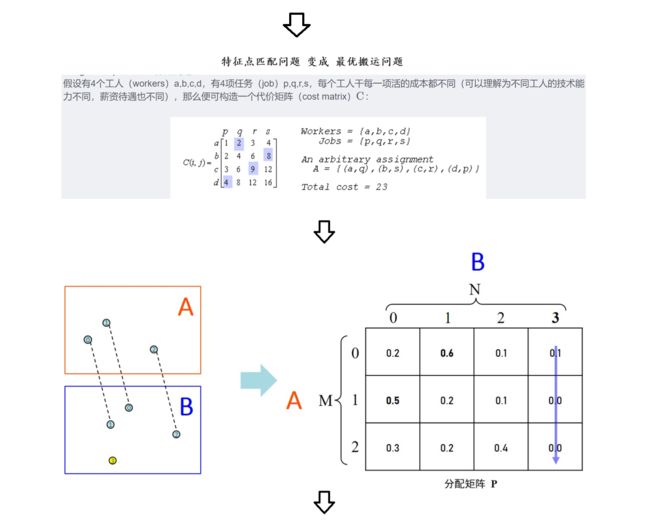
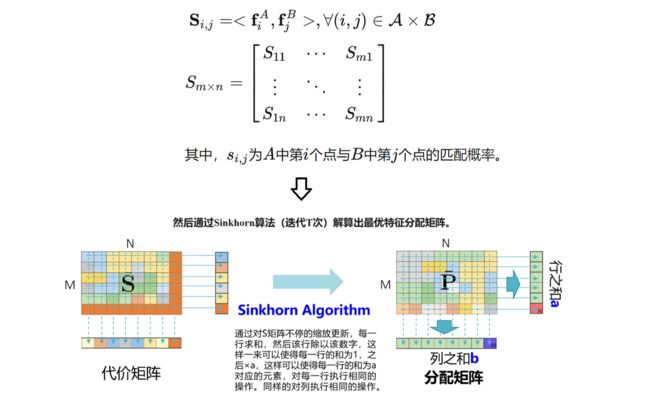
图匹配问题通常被公式化为二次分配问题,其是NP难的,需要昂贵、复杂并且因此不切实际的求解器[30]。对于局部特征,2000年代的计算机视觉文献[5,27,57]使用了许多启发式的手工成本,使其变得复杂和脆弱。Caetano等人[9]学习更简单的线性分配的优化成本,但只使用浅层模型,而我们的SuperGlue使用深度神经网络学习灵活的成本。与图匹配相关的是最优运输问题[63] -它是一个广义线性分配,具有有效而简单的近似解,即Sinkhorn算法[55,12,39]。
点云等集合的深度学习旨在通过聚合元素之间的信息来设计置换等不变函数。一些作品通过全局池化[70,40,15]或实例归一化[60,33,32]平等地对待所有元素,而其他作品则专注于坐标或特征空间中的局部邻域[41,66]。Attention [61,64,62,26]可以通过关注特定的元素和属性来执行全局和数据相关的局部聚合,因此更加灵活。通过观察到自我注意力可以被视为完整图上的消息传递图神经网络[23,4]的实例,我们将注意力应用于具有多种类型边缘的图,类似于[28,72],并使SuperGlue能够学习关于两组局部特征的复杂推理。
- The SuperGlue Architecture
动机:在图像匹配问题中,可以利用世界的一些规律:3D世界在很大程度上是平滑的,有时是平面的,如果场景是静态的,则给定图像对的所有对应关系都从单个对极变换导出,并且一些姿势比其他姿势更可能。此外,2D关键点通常是突出的3D点的投影,如角点或斑点,因此图像之间的对应关系必须遵守某些物理约束:
i)关键点可以在另一图像中具有至多单个对应关系
ii)由于检测器的遮挡和故障,一些关键点将不匹配。用于特征匹配的有效模型应旨在找到相同3D点的重投影之间的所有对应关系,并识别没有匹配的关键点。
我们将SuperGlue(见图3)表述为解决一个优化问题,其成本由深度神经网络预测。这减轻了对领域专业知识和启发式的需求-我们直接从数据中学习相关的先验知识。
在线性规划问题中,可能会有以下形式的约束条件:
1. Ax ≤ b(不等式约束)
2. Ax = b(相等约束)其中
- A 是代表约束条件的系数矩阵。
- x 是决策变量向量。
- b 是右侧的常量向量。
假设有一个相等约束 引入松弛变量 s 将其转换为不等式约束: Ax + s = b,其中 s 为非负。松弛变量 s 的作用是衡量在满足相等约束条件时有多少 "松弛 "或剩余。
如果 s 为零,表示完全满足相等约束条件。
如果 s 为正数,则表示平等约束条件没有得到充分利用,还存在一定的松弛。
如果 s 为负数,则表示违反了相等约束条件。
加入松弛变量后,线性规划求解器就能处理不等式,并找到尽可能满足相等约束条件的解决方案,即使这些约束条件因其他约束条件而无法完全满足。
总之,引入松弛变量是为了将相等约束条件转化为不等式约束条件,同时确保非负性,这样就可以使用不等式约束问题的标准技术来求解线性规划问题。