【学习笔记】CF1817F Entangled Substrings(基本子串结构)
前置知识:基本子串结构,SAM的结构和应用
学长博客
字符串理论比较抽象,建议直观的去理解它
子串 t t t的扩展串定义为 ext(t) : = t ′ \text{ext(t)}:=t' ext(t):=t′,满足 t t t是 t ′ t' t′的子串,且 occ(t) = occ(t’) \text{occ(t)}=\text{occ(t')} occ(t)=occ(t’)
基本性质:若 t = [ l : r ] , t ′ = [ l ′ : r ′ ] t=[l:r],t'=[l':r'] t=[l:r],t′=[l′:r′], t ′ ′ = [ l ′ ′ : r ′ ′ ] t''=[l'':r''] t′′=[l′′:r′′],使得 l ′ ≤ l ′ ′ ≤ l ≤ r ≤ r ′ ′ ≤ r ′ l'\le l''\le l\le r\le r''\le r' l′≤l′′≤l≤r≤r′′≤r′,则 ext(t”) = t ′ \text{ext(t'')}=t' ext(t”)=t′
子串 x , y x,y x,y等价当且仅当 ext(x) = ext(y) \text{ext(x)}=\text{ext(y)} ext(x)=ext(y)。然后,记录每个等价类的最长串作为代表元。
在 s [ l : r ] ↦ ( l , r ) s[l:r]\mapsto (l,r) s[l:r]↦(l,r)的作用下,在 y = x y=x y=x以上的点被等价类划分入若干个阶梯状集合,其中 g \text{g} g对应的阶梯 出现次数 为 occ(rep(g)) \text{occ(\text{rep(g)})} occ(rep(g))。
对于等价类 g g g个某个 完整阶梯,其完整的一行对应的子串集合与 T 0 T_0 T0的某个结点对应的子串集合相同,其完整的一列对应的子串集合与 T 1 T_1 T1(反串对应的后缀树)某个节点对应的子串集合相同,并且一一对应。
定义等价类 g g g的周长为其 一个 完整阶梯的行数列数之和,性质: ∑ g per(g) = O ( n ) \sum_g\text{per(g)}=O(n) ∑gper(g)=O(n)
比较抽象。不是很直观。
如何显式求出这个结构?
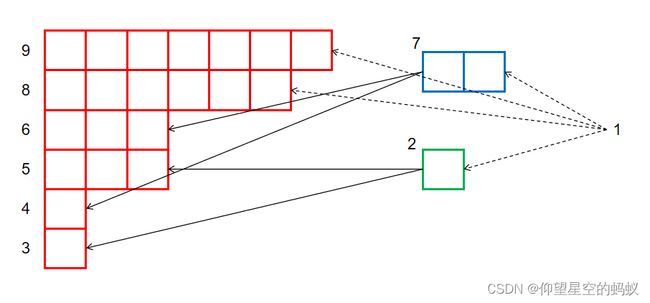
第一种方式:对于 T 0 T_0 T0的从父亲到儿子的树边,其从一行的左边界指向另一行的右边界;对于 T 1 T_1 T1的从父亲到儿子的树边,其从一行的上边界连向另一行的下边界。
例如, s = aababcd ‾ s=\underline{\text{aababcd}} s=aababcd,其对应的阶梯划分为:
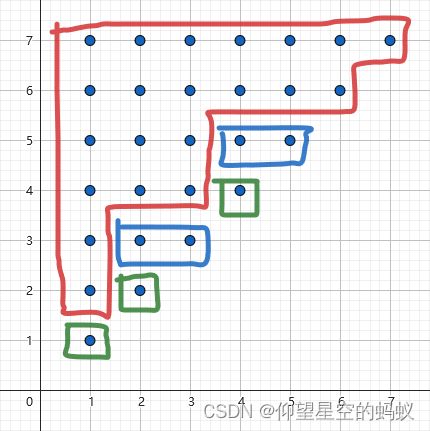
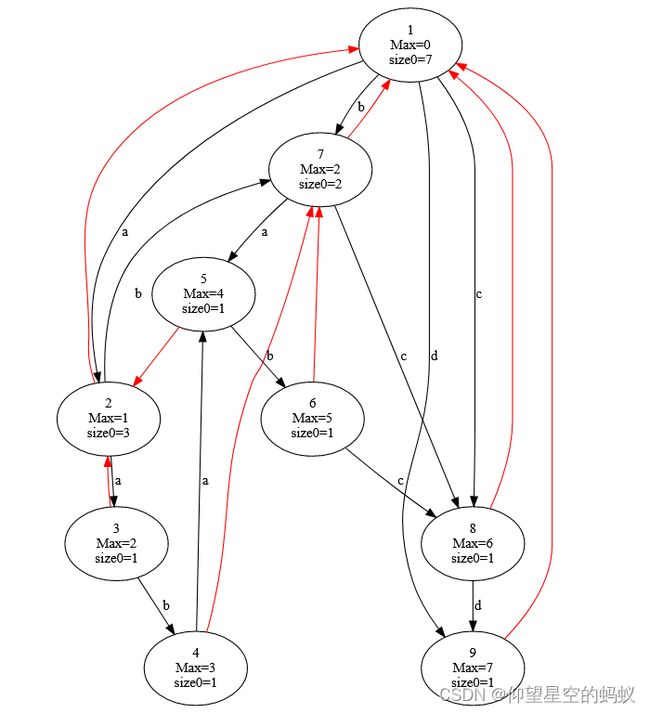
其对应的 S A M SAM SAM和 T 0 T_0 T0为:
其对应的连边为:
第二种方式(感觉更常用):对于 D A G DAG DAG上的一条边 ( u , v ) (u,v) (u,v),如果 occ(u) = occ(v) \text{occ(u)}=\text{occ(v)} occ(u)=occ(v),那么就将这条边标记为关键边。
性质:如果只保留关键边,那么每个点入度和出度都至多为一,因此我们得到了若干条关键链。显然,链的末尾就是代表元,一条链就代表了一个等价类
考虑这道题目在让我们干什么:可以发现一个字符串对 ( b 1 , b 2 ) (b_1,b_2) (b1,b2)是好的当且仅当满足以下条件:
1.1 1.1 1.1 b 1 , b 2 b_1,b_2 b1,b2在同一个等价类中
1.2 1.2 1.2 设 b 1 , b 2 b_1,b_2 b1,b2所在等价类中的代表元为 b b b,那么 b 1 , b 2 b_1,b_2 b1,b2在 b b b中出现的位置不交,且 b 1 b_1 b1在 b 2 b_2 b2左边
这样,我们对于每个 阶梯状物 统计答案即可。(建议数形结合,以及把下标搞清楚)
代表元的 len \text{len} len实际上表示阶梯状物左上角那个位置的横纵坐标之差。
复杂度 O ( n ) O(n) O(n)。
#include