算法思想之排序
你所知道的排序算法有哪些?
快速排序、冒泡排序,希尔排序,二分排序(二路归并)(nlogn),桶排序,堆排序,基数排序,插入O (n^2),选择排序
学习分组归类
插入&希尔&归并排序:递进学习
选择&冒泡&快速:递进递进学习
堆排序:树论高级篇里面
平常用的最多的排序算法又有哪些呢?他们的效率怎么样呢?
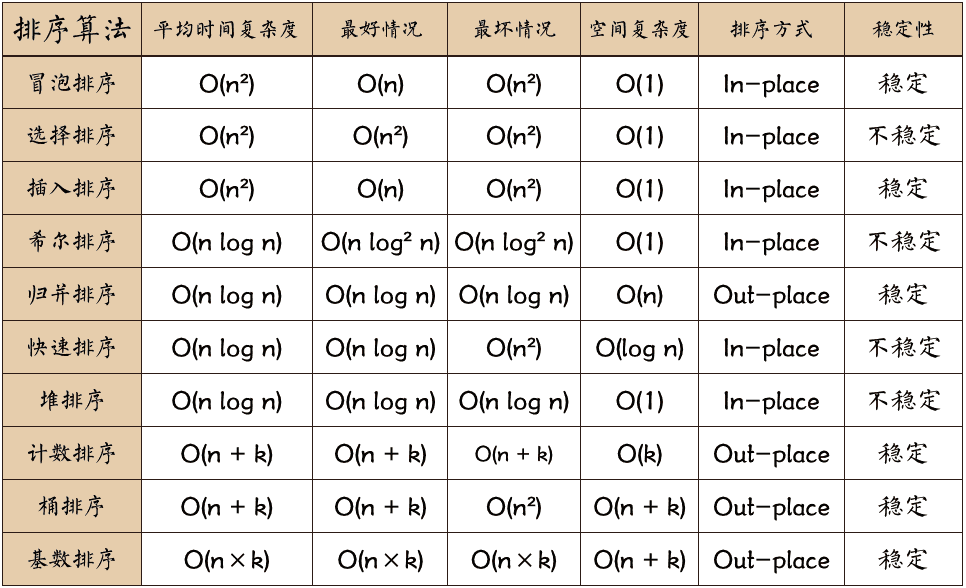
排序算法的好坏怎么区分?
- 时间效率
- 空间复杂度
- 比较次数&交换次数:排序肯定会牵涉到两个操作,一个比较是肯定的。交换
- 稳定性
插入&希尔&归并
插入排序
假设有个这样的问题:打扑克。
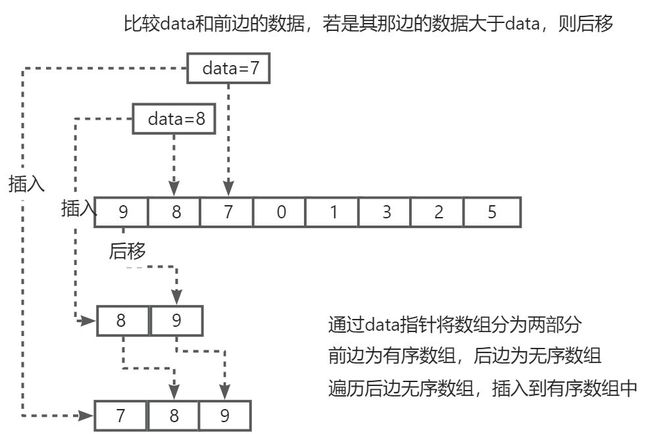
分成两部分:一部分是你手里的牌(已经排好序),一部分是要拿的牌(无序)。把一个无序的数列一个个插入到有序数列中。
一个有序的数组,我们往里面添加一个新的数据后,如何继续保持数据有序呢?我们只要遍历数组,找到数据应该插入的位置将其插入即可。
插入排序具体是怎么实现呢?具体步骤如下:
- 将数组分成已排序段和未排序段。初始化时已排序端只有一个元素
- 到未排序段取元素插入到已排序段,并保证插入后仍然有序
- 重复执行上述操作,直到未排序段元素全部加完
有几种数据结构,用什么数据结构来实现。数组,链表,2个数组
/**
* 1.将数组分成已排序段和未排序段。初始化时已排序端只有一个元素 【通过指针区分】
* 2.到未排序段取元素插入到已排序段,并保证插入后仍然有序
* 3.重复执行上述操作,直到未排序段元素全部加完
*
* @param arr
*/
public static void sort(int[] arr) {
// i=1,将第一个元素作为有序序列
for (int i = 1; i < arr.length; i++) {
int inserData = arr[i]; // 当前排序数据【临时变量】
// 当前元素与之前的有序序列对比插入
for (int j = i - 1; j >= 0; j--) {
if (arr[j] > inserData) { // 当前数>后边数
arr[j + 1] = arr[j]; // 后移,当前位置空缺
arr[j] = inserData; // 插入,当前位置
} else {
arr[j + 1] = inserData;
break; // 找到了插入位置
}
}
}
}
希尔排序
public void sort(int[] arr) {
for (int step = arr.length / 2; step >= 1; step /= 2) {
for (int i = step; i < n; i++) { // 为什么i要从1开始?
int data = arr[i];
int j = i - step;
for (; j >= 0; j -= step) {// 从尾到头 1+2+3+4+5+...+n=>
if (arr[j] > data) {
arr[j + step] = arr[j]; // 数据往后移动
} else { // 因为前面已经是排好序的 那么找到一个比他小的就不用找了,因为前面的肯定更小
break; // O(1) 如果这个break执行的越多 那么我是不是效率就越高?
}
}
arr[j + step] = data;
}
}
}
归并排序

/**
* 归:拆分数组
* 并:排序合并数组
*
* @param arr
* @param left
* @param right
*/
public static void megerSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
megerSort(arr, left, mid);
megerSort(arr, mid + 1, right);
// 合并
meger(arr, left, mid, right);
}
}
/**
* @param data 数组
* @param left 左指正
* @param mid 将数组区分为左右两部分
* @param right 右指针
*/
public static void meger(int data[], int left, int mid, int right) {
int temp[] = new int[data.length]; //借助一个临时数组用来保存合并的数据
int leftPoint = left;
int rightPoint = mid + 1;
int loc = left; //表示的是我们当前已经到了哪个位置了
while (leftPoint <= mid && rightPoint <= right) {
if (data[leftPoint] < data[rightPoint]) {
temp[loc++] = data[leftPoint++];
} else {
temp[loc++] = data[rightPoint++];
}
}
// 处理边界情况,while处理后左边或者右边最后一个元素一定没处理,或者某一边没处理【一边的数<另外一边最小的数】
// 处理左边
while (leftPoint <= mid) {
temp[loc++] = data[leftPoint++];
}
// 处理右边
while (rightPoint <= right) {
temp[loc++] = data[rightPoint++];
}
// 将排序好的数据覆盖回去
for (int i = left; i <= right; i++) {
data[i] = temp[i];
}
}
选择&冒泡&快排
选择排序
选择排序的思路和插入排序非常相似,也分已排序和未排序区间。但选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。但是不像插入排序会移动数组 选择排序会每次进行交换
/**
* 思路:
* 1. 将数组分为已排序和未排序区间【指针区分】
* 2. 每次排序找到未排序区间中最小的数
* 3. 将找到的数放入已排区间最后
*/
public static void selectionSort(int[] data) {
for (int i = 0; i < data.length; i++) {
int minPoint = i;
for (int j = i; j < data.length; j++) {
if(data[j]<data[minPoint]) minPoint = j;
}
// 交换位置
int tmp = data[i];
data[i] = data[minPoint];
data[minPoint] = tmp;
}
}
冒泡排序
public static void bubbleSort(int[] data) {
int last = data.length - 1;
for (int i = 0; i < last; last--) {
for (int j = i; j < last; j++) {
// 比较相邻两个数,交换位置
if (data[j] > data[j + 1]) {
int tmp = data[j];
data[j] = data[j + 1];
data[j + 1] = tmp;
}
}
}
}
快速排序
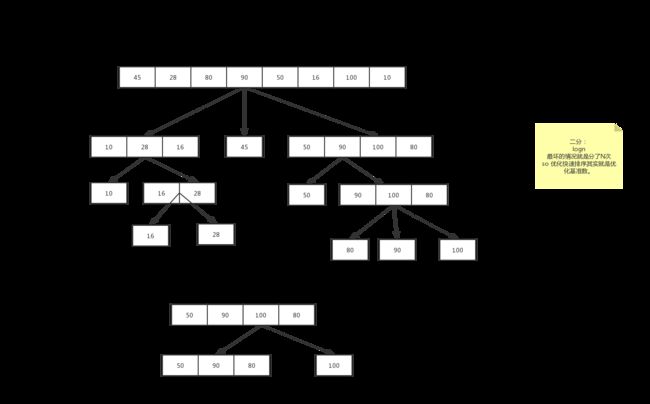
基准数:一般取要排序序列的第一个 45。
第一次排序基准数:
从后面往前找到比基准数小的数进行对换:10 28 80 90 50 16 100 45
从前面往后面找比基准数大的进行对换:10 28 45 90 50 16 100 80从后面往前找到比基准数小的数进行对换:10 28 16 90 50 45 100 80
从前面往后面找比基准数大的进行对换:10 28 16 45 50 90 100 80以基准数分为3部分,左边的比之小,右边比之大:{10 28 16} 45 {50 90 100 80}
到此第一次以45位基准数的排序完成
/**
* 快排:以基准数,交换比较数,直到基准数将数组分为三部分,左边<基准数,右边>基准数
*
* @param data
* @param left
* @param right
*/
public static void quickSort(Integer[] data, int left, int right) {
System.out.println("当前排序数组:" + Arrays.asList(data).subList(left, right + 1) + "\t基准数=" + data[left]);
// 基准数,取序列的第一个,不能用data[0]
int base = data[left];
// 基准数位置,表示的是从左边找的位置
int l = left;
// 表示从右边开始找的位置
int r = right;
while (l < r) {
// 从后面往前找比基准数小的第一个数
for (; l < r && data[r] >= base; r--) {
}
if (l < r) swap(data, l++, r);
// 从前面往前找比基准数大的第一个数
for (; l < r && data[l] <= base; l++) {
}
if (l < r) swap(data, l, r--);
}
String log = new StringBuffer().append("子排序结果:").append(Arrays.asList(data).subList(left, right + 1)).append("\r\n")
.append("总排序结果:").append(Arrays.toString(data)).append("\r\n")
.append("----------------------------------------------").toString();
System.out.println(log);
// 循环完成后, 左边<基准数<右边,左右递归快排
if (left < l) quickSort(data, left, l - 1);
if (l < right) quickSort(data, l + 1, right);
}
private static void swap(Integer[] data, int p1, int p2) {
int temp = data[p1];
data[p1] = data[p2];
data[p2] = temp;
}
测试用例
public static void main(String[] args) {
Integer[] arr = {45, 28, 80, 90, 50, 16, 100, 10};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
运行结果
当前排序数组:[45, 28, 80, 90, 50, 16, 100, 10] 基准数=45
子排序结果[10, 28, 16, 45, 50, 90, 100, 80]
总排序结果[10, 28, 16, 45, 50, 90, 100, 80]
----------------------------------------------
当前排序数组:[10, 28, 16] 基准数=10
子排序结果[10, 28, 16]
总排序结果[10, 28, 16, 45, 50, 90, 100, 80]
----------------------------------------------
当前排序数组:[28, 16] 基准数=28
子排序结果[16, 28]
总排序结果[10, 16, 28, 45, 50, 90, 100, 80]
----------------------------------------------
当前排序数组:[16] 基准数=16
子排序结果[16]
总排序结果[10, 16, 28, 45, 50, 90, 100, 80]
----------------------------------------------
当前排序数组:[50, 90, 100, 80] 基准数=50
子排序结果[50, 90, 100, 80]
总排序结果[10, 16, 28, 45, 50, 90, 100, 80]
----------------------------------------------
当前排序数组:[90, 100, 80] 基准数=90
子排序结果[80, 90, 100]
总排序结果[10, 16, 28, 45, 50, 80, 90, 100]
----------------------------------------------
当前排序数组:[80] 基准数=80
子排序结果[80]
总排序结果[10, 16, 28, 45, 50, 80, 90, 100]
----------------------------------------------
当前排序数组:[100] 基准数=100
子排序结果[100]
总排序结果[10, 16, 28, 45, 50, 80, 90, 100]
计数&基数
计数排序
算法的步骤如下:
- (1)找出待排序的数组中最大和最小的元素
- (2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- (3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- (4)反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
private static void countingSort(int[] datas, int maxDate) {
int[] counts = new int[maxDate + 1];
for (int data : datas) {
// 将排序数据作为下标,统计出现次数
counts[data]++;
}
// 排序
int sortedIndex = 0;
for (int i = 0; i < counts.length; i++) {
while (counts[i] > 0) {
datas[sortedIndex++] = i;
counts[i]--;
}
}
}
测试用例
public static void main(String[] args) throws Exception {
// 读取文件
String path = CountingSort.class.getClassLoader().getResource("200w.txt").getPath();
int[] datas = readText(path);
// 基数排序,数据最大值不会超过10w
countingSort(datas,100000);
// 写出文件
writeText("E:\\workspace_study\\technologist\\algorithm\\src\\main\\resources\\200w-csort.txt",datas);
}
private static int[] readText(String fileName) throws Exception {
InputStreamReader isr = new InputStreamReader(new FileInputStream(fileName), "UTF-8");
BufferedReader br = new BufferedReader(isr);
int data[] = new int[2100002];
int i = 0;
String str = null;
while ((str = br.readLine()) != null) {
double readDate = Double.valueOf(str);
data[i++] = (int) readDate * 100;
}
return data;
}
private static void writeText(String fileName, int[] datas) throws Exception {
File file = new File(fileName);
Writer out = new FileWriter(file);
for (int i = 0; i <= datas.length; i++) {
if (datas[i] > 0) {
for (int j = 0; j < datas[i]; j++) {
out.write(((double) (i / 100.0)) + "\r\n");
}
}
}
out.close();
}