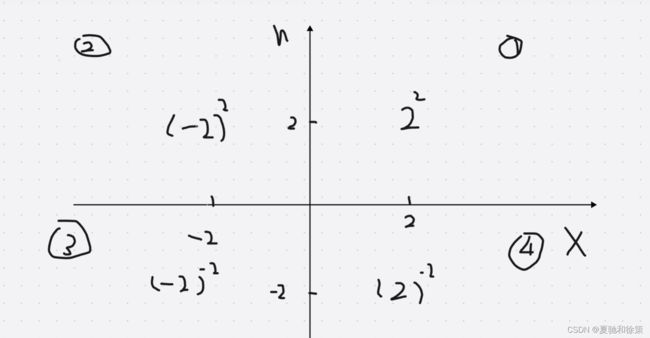Leetcode 50.Pow(x,n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3 输出:9.26100
示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0-231 <= n <= 231-1n是一个整数- 要么
x不为零,要么n > 0。 -104 <= xn <= 104
一、信息
1.实现数学中的幂函数。
2.三个示例
二、分析
条件1:告诉我此次的目的
条件2:告诉我这个函数结果保留小数点后五位
三、步骤
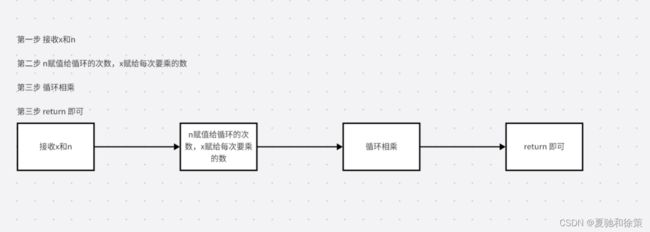
第一步 接收x和n
第二步 n赋值给循环的次数,x赋给每次要乘的数
第三步 循环相乘
第三步 return 即可
流程图:
四、遇到问题
1.由于n如果时负数那么我们显然累乘将失效,因为此时的x已经是它的倒数的累乘了而计算机其实根本不认识负幂数,所以我们得分类讨论。
分类讨论——四种情况:
分析:
1.情况1和情况2都不需要对x进行操作直接累乘就行了
2.情况3和情况4则首先需要判断n是否为负数如果是负数那么我们就先对x取倒数然后再进行累乘。
3.其次这样的话就不能直接把n赋给x了
五、实现
错误代码:
第一次错误——应该把num赋给i而不是原始的n:
double myPow(double x, int n){
int i,num=n;
double factor,answer=1;
factor=x;
if(num<0){
num=-num;
factor=1/x;
}
for(i=1;i<=n;i++){
answer=answer*factor;
}
return answer;
}当 n 是负数时,你已经将 num 转换为了正数,并且相应地调整了 factor。但是在循环中,你使用的是原始的 n,而不是调整后的 num。这会导致在 n 为负数时循环不执行。
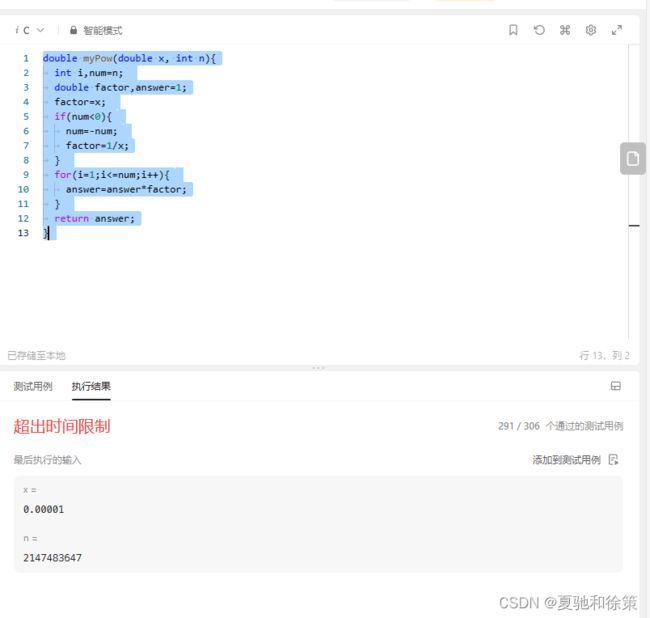
第二次错误——超时了+溢出:
double myPow(double x, int n){
int i,num=n;
double factor,answer=1;
factor=x;
if(num<0){
num=-num;
factor=1/x;
}
for(i=1;i<=num;i++){
answer=answer*factor;
}
return answer;
}当 n 是负数时,由于 int 类型的范围是 −2,147,483,648 到 2,147,483,647,所以当 n 等于 -2,147,483,648 时,转换为正数会导致溢出。为了避免这个问题,我应该使用 long long 类型来存储 num。
运行结果:
六、更正后我的答案
### 题目描述:
计算 `x` 的 `n` 次幂,即求 `x^n`。
### 思考过程:
1. **基本情况:**
- 如果 `n` 等于 0,对于任何 `x`(除了0),`x^0` 都是 1。
- 如果 `x` 等于 1 或 -1,并且 `n` 是负数,我们要计算的是 `1/x` 的正 `n` 次幂。
2. **负指数处理:**
- 如果 `n` 是负数,我们可以计算 `1/x` 的正 `n` 次幂。
3. **快速幂算法:**
- 快速幂算法的基本思想是将问题分解为更小的部分。例如,`x^8` 可以分解为 `(x^4)^2`。
- 我们可以利用这个性质,将 `n` 进行二进制分解,从而将原问题分解为若干个子问题,并利用已解决的子问题来解决更大的问题。
- 对于每一个二进制位,如果该位是1,我们就将当前的 `x` 乘到结果中。
### C语言实现:
#include
double myPow(double x, int n) {
// 使用 long long 避免整数溢出
long long N = n;
double ans = 1.0;
// 处理负指数的情况
if(N < 0) {
x = 1 / x;
N = -N;
}
// 快速幂算法
while(N > 0) {
if(N % 2 == 1) {
ans *= x; // 如果当前位是1,乘到结果中
}
x *= x; // 计算下一位
N /= 2; // 移动到下一位
}
return ans;
}
int main() {
double x = 2.0;
int n = -2;
printf("%lf\n", myPow(x, n)); // 输出:0.25
return 0;
} ### C++ 实现:
#include
using namespace std;
class Solution {
public:
double myPow(double x, long long n) {
if(n < 0) {
x = 1 / x;
n = -n;
}
double ans = 1.0;
while(n > 0) {
if(n & 1) {
ans *= x;
}
x *= x;
n >>= 1;
}
return ans;
}
};
int main() {
Solution s;
double x = 2.0;
int n = -2;
cout << s.myPow(x, n) << endl; // 输出:0.25
return 0;
} ### Java 实现:
public class Solution {
public double myPow(double x, int n) {
long N = n; // 使用 long 避免整数溢出
if (N < 0) {
x = 1 / x;
N = -N;
}
double ans = 1.0;
while (N > 0) {
if ((N & 1) == 1) {
ans *= x;
}
x *= x;
N >>= 1;
}
return ans;
}
public static void main(String[] args) {
Solution s = new Solution();
double x = 2.0;
int n = -2;
System.out.println(s.myPow(x, n)); // 输出:0.25
}
}这两个实现基本上是相同的,主要的区别在于语法。注意在Java实现中,我们使用了`long`来避免`int`溢出的问题,因为`int`在Java中是有固定大小的(32位)。在C++实现中,我们使用了`long long`来确保足够的位数,因为`int`和`long`在C++中的大小可能会因编译器和平台而异。
### 分析过程:
1. **时间复杂度:**
- 由于每次循环 `n` 都会除以 2,所以循环的次数是 `O(log n)`。
- 因此,这个算法的时间复杂度是 `O(log n)`。
2. **空间复杂度:**
- 这个算法只使用了几个变量来存储中间结果,因此空间复杂度是 `O(1)`。
### 结论:
这个快速幂算法是求幂问题的一种高效解决方案,它通过减少所需的乘法次数来提高效率,并具有较低的时间和空间复杂度。
Leetcode官方题解:
方法1:
class Solution { public: double quickMul(double x, long long N) { if (N == 0) { return 1.0; } double y = quickMul(x, N / 2); return N % 2 == 0 ? y * y : y * y * x; } double myPow(double x, int n) { long long N = n; return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N); } }; JAVA题解:
class Solution { public double myPow(double x, int n) { long N = n; return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N); } public double quickMul(double x, long N) { if (N == 0) { return 1.0; } double y = quickMul(x, N / 2); return N % 2 == 0 ? y * y : y * y * x; } }方法2:
C++题解:
class Solution { public: double quickMul(double x, long long N) { double ans = 1.0; // 贡献的初始值为 x double x_contribute = x; // 在对 N 进行二进制拆分的同时计算答案 while (N > 0) { if (N % 2 == 1) { // 如果 N 二进制表示的最低位为 1,那么需要计入贡献 ans *= x_contribute; } // 将贡献不断地平方 x_contribute *= x_contribute; // 舍弃 N 二进制表示的最低位,这样我们每次只要判断最低位即可 N /= 2; } return ans; } double myPow(double x, int n) { long long N = n; return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N); } };JAVA题解:
class Solution { public double myPow(double x, int n) { long N = n; return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N); } public double quickMul(double x, long N) { double ans = 1.0; // 贡献的初始值为 x double x_contribute = x; // 在对 N 进行二进制拆分的同时计算答案 while (N > 0) { if (N % 2 == 1) { // 如果 N 二进制表示的最低位为 1,那么需要计入贡献 ans *= x_contribute; } // 将贡献不断地平方 x_contribute *= x_contribute; // 舍弃 N 二进制表示的最低位,这样我们每次只要判断最低位即可 N /= 2; } return ans; } }
七、复盘对我分析思考过程的评价
大师的评价
我的代码和Leetcode题解的方法和代码的比较:
这个题解提供了两种解决方案:快速幂+递归和快速幂+迭代。
1. 快速幂 + 递归
这种方法采用分治的思想,每次将幂次减半。它用递归来实现,所以空间复杂度为O(logn)。这个方法的优势在于它的简洁性和直观性,对于理解问题很有帮助。但是,由于递归的开销,当n非常大时,可能会造成堆栈溢出。
2. 快速幂 + 迭代
这种方法将递归方法转化为迭代,消除了递归带来的堆栈溢出的风险,空间复杂度为O(1),比递归方法更加高效。它通过观察n的二进制表示中1的位置来计算x的幂,实际应用中更为常用。
对比你的方法
你的方法是直接循环n次来计算x的n次方。这种方法的时间复杂度是O(n)。当n非常大时,这会是一个很低效的算法。而且,你的方法没有处理n为负数的情况,直接循环会造成死循环。
总结
-
优势
- 快速幂方法,无论是递归还是迭代,时间复杂度都是O(logn),非常高效。
- 迭代方法的空间复杂度为O(1),对于空间敏感的场合非常适用。
-
劣势
- 递归方法的空间复杂度为O(logn),在幂次非常大时可能会有堆栈溢出的风险。
- 递归方法的理解和实现相对迭代方法更复杂一些。
-
改进你的方法
- 你的方法可以通过实现快速幂来减少时间复杂度到O(logn)。
- 处理n为负数的情况,可以通过计算x的正n次方,然后取倒数来得到结果。
八、反思总结
学到了什么:
通过这道题目,我们能学到以下几点:
### 1. **算法优化的重要性**
这道题目展示了相同问题的不同解决方案会有很大的效率差异。对于初学者来说,很容易想到暴力解法,即直接计算x的n次方,但这种方法的时间复杂度是O(n),在n很大时效率很低。而快速幂方法,无论是递归还是迭代,时间复杂度都可以优化到O(logn),大大提高了算法的效率。
### 2. **不同解法的优劣**
- **递归**:易于理解和实现,但可能有堆栈溢出的风险,且空间复杂度较高。
- **迭代**:迭代版本可以消除递归带来的堆栈溢出风险,且空间复杂度为O(1)。
学会权衡不同解法的优劣,并根据实际情况选择最合适的解法,是解决问题的关键。
### 3. **边界条件和特殊情况的处理**
这道题目要求处理n为负数的情况。处理特殊和边界情况是算法设计中很重要的一步,否则可能导致程序错误或者无法处理某些输入。
### 4. **二进制和位运算的应用**
快速幂算法利用了n的二进制表示来高效地计算x的n次方。通过观察n的二进制表示中1的位置,我们可以减少不必要的计算。这显示了二进制和位运算在算法设计中的重要应用。
### 5. **算法设计的灵活性和多样性**
这道题目通过展示递归和迭代两种不同的解法,体现了算法设计的灵活性和多样性。掌握多种解法并能灵活运用,可以帮助我们更好地解决实际问题。
### 6. **数学知识的运用**
这个问题还涉及到一些数学知识,比如指数和幂的性质。对基础数学知识的理解能帮助我们更好地理解问题和设计算法。
### 总结
综上所述,这道题目不仅能帮助我们学习和巩固快速幂算法,还能够加深我们对于递归、迭代、位运算、数学知识运用等方面的理解,让我们更加灵活和深入地去思考和解决问题。