Diffusion Autoencoders: Toward a Meaningful and Decodable Representation

Diffusion Autoencoders: Toward a Meaningful and Decodable Representation (Paper reading)

Konpat Preechakul, VISTEC, Thailand, CVPR22 Oral, Cited:117, Code, Paper

1. 前言

扩散概率模型 (DPM) 在图像生成方面取得了显着的质量，可与 GAN 相媲美。但是与 GAN 不同，DPM 使用一组潜在变量，这些变量缺乏语义含义，不能作为其他任务的有用表示。本文探索了使用DPM进行表示学习的可能性，并试图通过自动编码提取输入图像的有意义和可解码的表示。我们的关键思想是使用可学习的编码器来发现高级语义，并使用 DPM 作为解码器来对剩余的随机变化进行建模。我们的方法可以将任何图像编码为两部分潜在编码，其中第一部分在语义上有意义且线性，第二部分捕获随机细节，允许近乎精确的重建。这种能力使目前阻碍基于 GAN 的方法（例如真实图像的属性操作）的挑战性应用程序成为可能。我们还表明，这种两级编码提高了去噪效率，并自然地促进了各种下游任务，包括few-shot条件采样。

2. 整体思想

本文是利用扩散模型做图像属性编辑的一份工作。主要思想是把扩散模型作为自编码器的解码器，然后将自编码器的编码器输出$z_{sem}$作为条件，通过训练这个自编码器，$z_{sem}$就会类似于GANs或VAEs中的潜在code。我们对这个code做出改变就可以实现对图像的编辑。

---

一些疑问？建议看完文章后再看这部分，如果你也有跟我同样的疑问：

1. 1. 语意编码器是如何训练的：本文的语意编码器其实就是一个U-Net的Encoder把$x_0$编码为512维的1维向量。Fig7(a)是conditional DDIM的框架，它是条件的！这个条件是可学习的，也就是$z_{sem}$，训练DDIM的过程中，就会优化语意编码器的参数。不要被自编码器中的Decoder误解，这个Decoder就是DDIM整个U-Net，包含了U-Net中的Enc-Dec。
2. 2. 第4小节的采样，或者说latent DDIM是干啥的：本文虽然是做人脸编辑的，但该方法同样也是一个生成模型，也就是说我们通过随机的$z_{sem}$是可以生成图像的。因此这里训练了一个latent DDIM用来随机生成$z_{sem}$，然后就可以通过backbone的conditional DDIM采样得到图像。Fig9主要说明了这个问题。
3. 3. 随机编码器是干啥的：随机编码器其实是图像插值和编辑的采样过程，与第二个问题不同。第二个是生成，这个是编辑！我们通过随机编码器的公式进行迭代就能采样得到编辑后的图片。注意每一步的$x_t$都是上一步通过计算得到的。具体看5.1小节，$x_T$是随机采样的。
4. 4. 是如何对真实图像进行插值和编辑的：本文的工作本质是一个基于扩散模型的自编码器，与其他工作类似，同样是修改$z_{sem}$来达到这个目的。但是扩散模型是一个生成模型，如何修改$z_{sem}$来采样的呢？一个不同点是扩散模型的输入中有一个$x_T$，如果是插值的话，我们也需要插值一个新的$x_T$，而编辑的话$x_T$就一个。然后，只需要对$x_T$不断去噪就可，这里条件是$z_{sem}$。
5. 5. 有两个编码器，一个是语意编码器和conditional DDIM中U-Net的编码器，能否只用语意编码器来重构图像：这就有点像自编码器通过laten code来重构图像了，但是本文$z_{sem}$设计的方式是加在整个conditional DDIM的U-Net中，不使用$x_T$的话，这种结构确实无法重建，本人认为。

3. 方法

在本文中，我们质疑dpm是否可以作为一个很好的表征学习器。具体来说，我们试图提取图像的有意义和可解码的表示，包含高级语义，但允许图像的近乎精确的重建。我们的探索主要集中在扩散模型上，但这些贡献也适用于基于分数的模型。学习表征的一种方法是通过自动编码器。存在一种DPM，它可以作为编码器-解码器，通过反向运行生成过程，将任意输入图像x0转换为空间潜在变量xT。然而，由此产生的潜在变量缺乏高级语义和其他理想的特性，例如解纠缠、紧凑性或在潜在空间中执行有意义的线性插值的能力。或者，可以使用经过训练的GAN提取表示，使用所谓的GAN反演[28,58]，该方法针对再现给定输入的潜在代码进行优化。尽管生成的代码具有丰富的语义，但这种技术很难忠实地重建输入图像。为了克服这些挑战，我们提出了一种基于扩散的自编码器，它利用强大的dpm进行可解码表示学习

为了追求有意义的潜码，我们设计了一个条件DDIM图像解码器$p(x_{t-1}|x_t,z_{sem})$，它以附加的潜变量$z_{sem}$为条件，以及一个语义编码器$z_{sem}=En{c}_{\phi }(x_0)$，它学习将输入图像$x_0$映射到一个语义有意义的$z_{sem}$。这里，条件DDIM解码器将隐变量$z=(z_{sem},x_T)$作为输入(这里的$x_T$的维度和$z_{sem}$是相同的!)，该隐变量由高级的“语义”子码$z_{sem}$和低级的“随机”子码$x_T$组成，通过反转DDIM的生成过程来推断。在这个框架中，DDIM既充当解码器，又充当随机编码器。概览如图2所示。

图2。我们的扩散自动编码器概述。自动编码器由一个“语义”编码器组成，它将输入图像映射到语义子码$(x_0\to z_{sem})$，以及一个条件DDIM，它既充当“随机”编码器$(x_0\to x_T)$，也充当解码器$((z_{sem},x_T)\to x_0)$。在这里，$z_{sem}$捕获高级语义，而$x_T$捕获低级随机变化，它们一起可以以高保真度解码回原始图像。为了从该自编码器中采样，我们将潜在DDIM拟合到$z_{sem}$和样本$(z_{sem},x_T\sim N(0,I))$的分布中进行解码。

与其他使用空间条件变量(例如，2D潜在映射)的条件dms不同，我们的$z_{semi}$是维数d = 512的非空间向量，类似于StyleGAN中的样式向量，允许我们编码不特定于任何空间区域的全局语义。我们的目标之一是学习一个语义丰富的潜在空间，允许平滑插值，类似于gan学习的那些，同时保持扩散模型擅长的重建能力。

3.1 基于扩散的解码器

我们的条件DDIM解码器接收输入$z=(z_{sem},x_T)$来产生输出图像。该解码器是一个条件DDIM，它对$p_{\theta }(x_{t-1}|x_t,z_{sem})$建模，以匹配推理分布$q(x_{t-1}|x_t,x_0)$，并使用以下反向(生成)过程:
$$p_{\theta }(x_{t-1}|x_t,z_{sem})=\left\{\begin{array}{c}N(f_{\theta }(x_1,1,z_{sem}),0)ift=1\\ q(x_{t-1}|x_t,f_{\theta }(x_t,t,z_{sem}))otherwise\end{array}\right\}$$
其中$f_{\theta }=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\sqrt{1-{\alpha }_t}{ϵ}_{\theta }(x_t,t,z_{sem}))$。这里${ϵ}_{\theta }$是一个U-Net，通过$L_{simple}=||{ϵ}_{\theta }(x_t,t,z_{sem})-{ϵ}_t|{|}_2^2$损失进行训练。训练阶段，随机潜在变量$x_T$不是必须的。我们使用自适应组归一化层(AdaGN)来约束UNet，我们的AdaGN条件为:
$$AdaGN(h,t,z_{sem})=z_s(t_s\text{GroupNorm}(h)+t_b)$$
其中，$z_s\in R^c=\text{Affine}(z_{sem})$且$(t_s,t_b)\in R^{2\times c}=MLP(\psi (t))$是具有正弦编码函数$\psi$的多层感知器的输出。这些层在整个UNet中使用。下图b中MLP分别有一个$\times$和$+$对应着上式的$t_s$和$t_b$，紧接着乘上一个$z_s=MLP(z_{sem})$。

3.2 语义编码器

语义编码器$Enc(x_0)$的目标是将输入图像总结为一个描述向量$z_{sem}=Enc(x_0)$，其中包含必要的信息，以帮助解码器$p_{\theta }(x_{t-1}|x_t,z_{sem})$去噪和预测输出图像。我们不假设这个编码器有任何特定的架构;然而，在我们的实验中，这个编码器与我们的UNet解码器的前半部分共享相同的架构。使用信息丰富的$z_{sem}$调节DDIM的一个好处是更有效的去噪过程，这将在5.5节中进一步讨论。

3.3 随机编码器

除了解码之外，我们的条件DDIM还可以通过反向运行其确定性生成过程，将输入图像$x_0$编码为随机编码：
$$x_{t+1}=\sqrt{{\alpha }_{t+1}}{f}_{\theta }(x_t,t,z_{sem})+\sqrt{1-{\alpha }_{t+1}}{ϵ}_{\theta }(x_t,t,z_{sem})$$
我们可以把这个过程看作是一个随机编码器，因为$x_T$被鼓励只编码$z_{sem}$遗漏的信息，而$z_{sem}$压缩随机细节的能力有限。通过使用语义和随机编码器，我们的自动编码器可以捕获输入图像的最后一个细节，同时也为下游任务提供高级表示$z_{sem}$。请注意，随机编码器在训练期间没有使用，而是用于计算需要精确重建或反演的任务的$x_T$，例如真实图像处理。

4. 扩散自编码器采样

通过将解码器调节为$z_{sem}$，扩散自编码器不再是生成模型。因此，为了从我们的自编码器中采样，我们需要一个额外的机制来从潜在分布中采样$z_{sem}\in R^d$。虽然VAE是一个很好的选择，但是很难在保留潜在代码中的丰富信息和保持VAE的采样质量之间取得平衡。GAN是另一种选择，尽管它使训练稳定性复杂化，而训练稳定性是dpm的一个主要优势。这里，我们选择对$z_{sem}=En{c}_{\phi }(x_0)$， $x_0\sim p(x_0)$的潜在分布拟合另一个DDIM，称为潜在DDIM $p_{\omega }(z_{sem},t-1|z_{sem},t)$。与式5和式6类似，通过对$\omega$优化$L_{latent}$来训练潜在的DDIM:
$$L_{latent}=\sum _{t=1}^T{\mathbb{E}}_{z_{sem},{ϵ}_t}[||{ϵ}_{\omega }(z_{sem},t)-{ϵ}_t|{|}_1]$$
式中$t\in R^{d}N(0,I)$， $z_{sem,t}=\sqrt{{\alpha }_t}{z}_{sem}+\sqrt{1-{\alpha }_t}{ϵ}_t$，T与DDIM图像解码器中的T相同。对于Llatent，我们经验地发现L1比L2损耗更有效。与1D/2D图像不同，对于非空间数据，没有完善的DPM架构，但我们发现具有跳过连接的深度mlp(10-20层)表现相当好。结构如下：

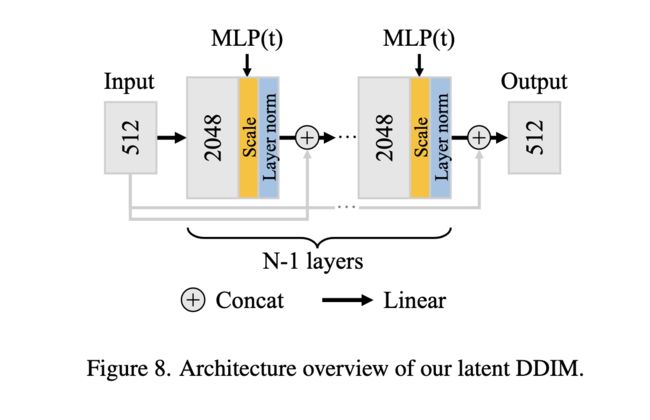
我们首先通过$L_{simple}$训练语义编码器(φ)和图像解码器(θ)，直到收敛。然后，在固定语义编码器的情况下，通过$L_{latent}$训练潜在的DDIM (ω)。在实际应用中，由潜在DDIM建模的潜在分布首先被归一化，使其具有零均值和单位方差。因此，从扩散自编码器中进行无条件采样是通过从潜在的DDIM中采样$z_{sem}$并对其进行非正态化，然后采样$x_T\sim N(0,I)$，最后使用解码器解码$z=(z_{sem},x_T)$来完成的。

我们选择对潜在DDIM进行事后训练有几个实际的原因。首先，由于训练潜在的DDIM只需要整个训练时间的一小部分，因此事后训练可以使用相同的扩散自编码器对不同的潜在DDIM进行快速实验。另一个原因是通过不施加任何约束来保持$z_{sem}$尽可能具有表现力，例如VAE中的先验损失，这会损害潜在变量的质量。

5. 实验

现在我们开始评估学习到的潜在空间的属性，并演示新的功能，比如属性操作和条件生成。为了公平比较，我们实验中的DDIM基线是Guided Diffusion的改进架构重新实现的DDIM，其UNet超参数与我们的解码器相同。简而言之，DDIM基线与我们的解码器类似，只是它不占用$z_{sem}$。

5.1 潜在编码捕获高级语义和低级随机变化

为了证明高级语义主要在$z_{sem}$中捕获，而在$x_T$中捕获很少，我们首先从输入图像$x_0$计算语义子码$z_{sem}=Enc(x_0)$。对于随机子码$x_T$，我们将对该子码进行多次采样$(x_T^i\sim N(0,I))$并解码多个$z^i=(z_{sem},x_T^i)$，而不是从输入中推断它。图3显示了给定相同$z_{sem}$时由不同$x_T$引起的变化，以及不同$z_{sem}$引起的变化。

结果表明，在固定的$z_{sem}$下，随机子码$x_T$只影响次要的细节，如头发和皮肤细节、眼睛或嘴巴，而不会改变整体外观。通过改变$z_{sem}$，我们得到了完全不同的人，他们有不同的面部形状、光照和整体结构。

5.2 语义上有意义的潜在插值

有用的潜在空间的一个理想特性是能够通过潜在空间的简单线性变化来表示图像中的语义变化。例如，通过沿着连接任意两个潜在代码的直线移动，我们期望在对应的两个图像之间平滑变形。在图4d和图1中，我们将两幅输入图像编码为$(z_{sem}^1,x_T^1)$和$(z_{sem}^2,x_T^2)$，然后解码$z(t)=(Lerp(z_{sem}^1,z_{sem}^2;t),Slerp(x_T^1,x_T^2;t))$对于$t\in [0,1]$的各种值，其中$z_{sem}$采用线性插值$y=a{x}_1+(1-a)x_2$，$x_T$采用球面线性插值:
$$x_T^a=\frac{sin((1-a)\theta )}{sin(\theta )}{x}_t^1+\frac{sin(a\theta )}{sin(\theta )}{x}_T^2\theta =arccos(\frac{(x_T^1{)}^{\text{T}}{x}_T^2}{||x_T^1||||x_T^2||})$$

与产生非平滑过渡的DDIM相比，我们的方法在两个端点之间逐渐改变头部姿态、背景和面部属性。StyleGAN在W和W+空间中的插值结果都是平滑的，但两个端点与输入图像不相似，而我们的和DDIM的几乎完全匹配真实的输入图像。

5.3 真实图像的属性编辑

评估图像语义与潜在空间中的线性运动或可分性之间关系的另一种方法是通过在特定方向上移动图像的潜在$z_{sem}$并观察图像的变化。通过从在目标属性（例如微笑）的负面和正面图像的潜在编码上训练的线性分类器的权重向量中找到这样的方向，该操作因此改变了图像中的语义属性。这项任务有专门的技术，但在这里，我们的目标是通过使用最简单的线性运算来展示我们潜在空间的质量和适用性。

我们使用来自CelebA-HQ的图像和属性标签训练线性分类器，并在CelebA-HQ和FFHQ上进行测试，见图5。为了评估我们操纵的结果的质量，我们将它们的分布与具有目标积极属性（如微笑）的真实图像的分布进行比较。我们的操作是通过沿着目标方向$w$线性移动$z_{sem}$来完成的，通过训练线性分类器（逻辑回归）$y=w^{T}z+b$来使用标记的数据集预测目标属性。随机子编码$x_T$保持不变。给定$z$，其操纵版本由解码$z\prime =z+sw$产生，其中$s\in R$控制操纵程度。对于这个实验，每个输入图像将由不同的$s_i$操纵，以便操纵的结果达到目标属性的相同程度（例如，类似的大微笑）。具体而言，我们选择$s_i$，使其$z{\prime }_i$的logit置信度等于所有真实正图像的中值置信度：
$$s_i=\frac{mdian-b-z_i^{T}w}{w^{T}w}$$

5.4 自编码重构质量

尽管自编码器的良好重建质量不一定是良好表示学习的指标，但这一特性在许多应用中起着重要作用，例如需要精确编解码能力的压缩或图像处理。对于这些任务，传统的依赖于MSE或L1损失函数的自编码器表现不佳，并且产生模糊的结果。更先进的自编码器结合了感知损失和对抗损失，例如VQGAN，或者依赖于潜在变量的层次结构，例如NVAE ， VQ-VAE2。我们的扩散自编码器是一种替代设计，它产生具有意义和紧凑的语义子码的合理大小的潜在代码，并与最先进的自编码器竞争。关键是我们的两级编码，它将不可压缩的随机细节的重建委托给我们的条件DDIM。

在表1中，我们评估了1)我们的扩散自编码器，2)DDIM， 3)预训练的StyleGAN2(通过两种类型的反演)，4)VQ-GAN ， 5) VQ-VAE2 ， 6) NVAE的重建质量。DDIM和我们的算法都是在130M张图像上进行训练，并使用T=100进行解码。所有这些模型都在FFHQ上进行了训练，并在来自CelebA-HQ的30k张图像上进行了测试。对于我们的方法和DDIM，我们编码了尺寸为128×128的缩小测试图像，并将它们解码回来。对于其他的，我们在256×256上使用公开可用的预训练网络，并在比较之前将结果缩小到相同的128×128。对于StyleGAN2，我们在测试图像的W和W+空间进行反演，并使用优化后的编码进行重构。评估指标为SSIM(↑)、LPIPS(↓)和MSE。NVAE获得了最低的LPIPS和MSE得分，尽管它需要比其他方法大几个数量级的潜在维度。除了NVAE之外，我们的扩散自编码器在所有指标上都优于其他模型，并且在T =100步时只需要T=20步就可以超过DDIM。

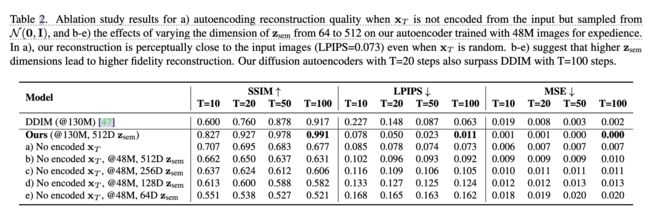
此外，我们进行了消蚀研究，以研究1)仅从输入编码$z_{sem}$，但从N (0, I)采样$x_T$进行解码时的重建质量(表2.a)，以及2)为了方便起见，将$z_{sem}$的维度从64改变到512(表2.b-e)对使用48M图像训练的自编码器的影响。所有配置(a)-e)都产生真实的结果，但在保真度上有所不同，其中潜在维数越高越好。对于配置a)使用512D $z_{sem}$，即使$x_T$是随机的，重构仍然在感知上接近LPIPS测量的输入图像。我们使用小64D $z_{sem}$的重构已经与512D潜在空间中的StyleGAN2反演相当，这表明我们的扩散自编码器精通压缩。

5.5 更快的采样过程

使用来自$z_{sem}$的语义信息调节去噪过程的一个有用的好处是生成更快。dpm需要许多生成步骤的一个主要原因是，当T足够大(~ 1000)时，dpm只能使用高斯分布来近似p(xt−1|xt)。最近提高采样速度的尝试集中在寻找更好的采样间隔或噪声调度，或者使用更有效的求解器来求解基于分数的ODE。我们的扩散自编码器并不旨在直接解决这个问题，也不能在与无法访问目标样本的生成模型相同的上下文中进行比较。考虑一个场景，其中$x_0$是去噪网络已知的。噪声预测任务将变得微不足道，并且无论时间步长多少，$q(x_{t-1}|x_t,x_0)$都是高斯分布。由于我们的扩散自编码器对分布$p(x_{t-1}|x_t,z_{sem})$建模，因此当$z_{sem}$捕获了大量关于$x_0$的信息时，$p(x_{t-1}|x_t,z_{sem})$比$p(x_{t-1}|x_t)$更接近$q(x_{t-1}|x_t,x_0)$。图6显示，扩散自编码器能够以比DDIM更少的步骤更准确地预测$x_0$，并且在表4中具有相同时间步长T的四个不同数据集上产生更好的图像质量。

5.6 潜在DDIM记得它的输入吗?

为了验证我们的扩散自编码器和潜在DDIM是否可以生成新的样本，而不是简单地记住输入，我们生成图像样本，并将它们与训练集中最近的临近进行比较(图9)。为了找到最近的临近，我们使用了三个不同的指标:1)图像空间中的最低LPIPS， 2)图像空间中的最低MSE, 3)语义子空间($z_{sem}$)中的最低MSE。我们发现我们的自动编码器可以从训练集生成完全不同的图像，这表明没有记忆问题。对于顶部的每个采样图像，我们根据LPIPS、图像空间中的MSE和语义子码zsem空间中的MSE从训练集中找到最接近的图像。采样图像与任何训练图像都不太相似，这表明我们的潜在DDIM并没有记住输入样本。

5.7 随机子码中编码了什么?

图10显示了在给定相同$z_{sem}$的情况下，由不同的$x_T$引起的随机变化。我们还计算了这些变化的均值和标准差。所有生成的图像看起来都很逼真，$x_T$只改变了一些小细节，比如头发图案，同时保持整体结构不变。

6. 限制和讨论

在对训练分布之外的图像进行编码时，由于DDIM的高维随机子码，我们的扩散自编码器仍然可以很好地重建图像。然而，推断的语义子码和随机子码都可能落在学习分布之外，导致不能再解释或内插的不良表示。虽然我们选择使用非空间潜码适合学习全局语义，但某些图像和空间推理任务可能需要更精确的局部潜变量。对于这些任务，结合二维潜在地图可能是有益的。

对于图像生成，StyleGAN的一个独特功能是我们的扩散自动编码器所缺乏的，即控制特定比例生成的能力。在生成速度方面，我们的框架大大减少了从DDIM中获得高质量样本所需的时间步长，但仍然缺乏gan，后者只需要单个生成器通过即可生成图像。

总之，我们提出了扩散自编码器，它可以从输入图像中分别推断语义和随机信息。与dms和高保真自编码器(如NVAE)相比，我们的潜在表示允许近乎精确的解码，同时包含对下游任务很有用的紧凑语义。这些属性使各种实时图像编辑任务的简单解决方案不需要gan及其容易出错的反演。我们的框架还提高了去噪效率，并保留了dpm的竞争性无条件采样。