顺序表的实现和练习

杂谈：

有些数据结构（C语言实现）的教材/教程中会使用C++中引用的语法，引用确实在形式上比指针简洁，这样做无非是为了避免后续对二级指针的使用。

我认为既然使用C语言实现数据结构，那么指针就不应该是门槛。增加了引用的C到底是C还是C++呢？如果使用C++完全可以用类实现数据结构，而不是使用兼容C的低级语法。

C语言实现数据结构重要前置知识：指针、结构体、动态内存管理、（递归、函数栈帧...）。

顺序表实现（动态版本）

用C实现顺序表结构（动态版本，支持自动扩容），及相关操作函数：初始化、销毁、打印、插入（任意位置、头插、尾插）、删除（任意位置、头删、尾删）、查找、修改。

注：本文（包括后续数据结构实现）函数命名均采用C++STL的命名风格

定义顺序表及函数声明

在SeqList.h头文件中定义顺序表结构及声明相关函数：

#include 
#include 
#include 

typedef int SLDataType; // 顺序表数据类型
typedef struct SeqList  // 顺序表结构
{
	SLDataType* a; // 动态数组，存放数据元素
	int size;      // 元素个数
	int capacity;  // 数组容量
}SL;

void SLInit(SL* psl);   // 顺序表初始化
void SLDestroy(SL* psl);// 销毁顺序表

// 对数据的管理:增删查改 
void SLPrint(SL* psl); // 打印顺序表
void SLPushBack(SL* psl, SLDataType x); // 尾插元素
void SLPushFront(SL* psl, SLDataType x);// 头插元素
void SLPopFront(SL* psl);// 头删
void SLPopBack(SL* psl); // 尾删

// 顺序表查找
int SLFind(SL* ps, SLDataType x);
// 顺序表在pos位置（下标）插入x
void SLInsert(SL* ps, int pos, SLDataType x);
// 顺序表删除pos位置（下标）的值
void SLErase(SL* ps, int pos);
// 顺序表修改pos位置的值
void SLModify(SL* psl, int pos, SLDataType x);

函数定义

在SeqList.c文件中定义顺序表操作函数，为方便演示，所有函数将单独展示：

初始化

#include "SeqList.h"
void SLInit(SL* psl)
{
	assert(psl);// 断言psl是否为空指针

	psl->a = (SLDataType*)malloc(sizeof(SLDataType) * 4);// 初始容量设置为4
	if (psl->a == NULL) //动态申请失败，结束函数
	{
		perror("malloc fail");
		return;
	}

	psl->capacity = 4;
	psl->size = 0;
}

销毁

注：对顺序表指针的销毁应由使用者操作 free(psl); psl = NULL;

void SLDestroy(SL* psl)
{
	assert(psl);

	free(psl->a); // 释放动态数组
	psl->a = NULL;// 指针置空
	psl->size = psl->capacity = 0;// 个数、容量置0
}

打印

void SLPrint(SL* psl)
{
	assert(psl);

	for (int i = 0; i < psl->size; i++)
	{
		printf("%d ", psl->a[i]);
	}
	printf("\n");
}

检查容量

容量不够则扩容2倍

void SLCheckCapacity(SL* psl)
{
	assert(psl);

	if (psl->size == psl->capacity)// 顺序表已满，需要扩容
	{
		SLDataType* tmp = (SLDataType*)realloc(psl->a, sizeof(SLDataType) * psl->capacity * 2);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}

		psl->a = tmp;
		psl->capacity *= 2;
	}
}

插入

void SLInsert(SL* psl, int pos, SLDataType x)
{
	assert(psl);

	assert(0 <= pos && pos <= psl->size);// 断言pos是否合法，可在原范围[0,size)和下一位置size插入

	SLCheckCapacity(psl);

	int end = psl->size - 1;
	while (end >= pos) 
	{
		psl->a[end + 1] = psl->a[end];// 元素向后移动一位
		--end;
	}

	psl->a[pos] = x;// pos位置插入x
	psl->size++;
}

删除

void SLErase(SL* psl, int pos)
{
	assert(psl);

	assert(0 <= pos && pos < psl->size);// 只能删除原范围数据[0,size)

	int start = pos + 1;
	while (start < psl->size)
	{
		psl->a[start - 1] = psl->a[start];// 元素向前移动一位
		++start;
	}

	psl->size--;
}

尾插

在顺序表末尾增加一个元素

void SLPushBack(SL* psl, SLDataType x)
{
	assert(psl);

	SLInsert(psl, psl->size, x);
}

头插

在顺序表第一个元素前插入一个元素

void SLPushFront(SL* psl, SLDataType x)
{
	assert(psl);

	SLInsert(psl, 0, x);
}

尾删

删除顺序表最后一个元素

void SLPopBack(SL* psl)
{
	assert(psl);

	SLErase(psl, psl->size - 1);
}

头删

删除顺序表第一个元素

void SLPopFront(SL* psl)
{
	assert(psl);

	SLErase(psl, 0);
}

查找

查找元素第一个位置，返回其下标（未找到返回-1）

int SLFind(SL* psl, SLDataType x)
{
	assert(psl);

	for (int i = 0; i < psl->size; i++)
	{
		if (psl->a[i] == x)
		{
			return i;
		}
	}

	return -1;
}

修改

void SLModify(SL* psl, int pos, SLDataType x)
{
	assert(psl);

	assert(0 <= pos && pos < psl->size);

	psl->a[pos] = x;// 修改pos位置数据
}

测试

在test.c文件中定义函数或直接在main函数中测试顺序表功能，建议每实现一部分功能就进行相关测试。如果实现完顺序表的所有操作函数在去测试，不容易发现错误。

1 尾插测试

void TestSeqList1()
{
	SL s;
	SLInit(&s);

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 5);

	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

2 头插测试

void TestSeqList2()
{
	SL s;
	SLInit(&s);

	SLPushFront(&s, 1);
	SLPushFront(&s, 2);
	SLPushFront(&s, 3);
	SLPushFront(&s, 4);
	SLPushFront(&s, 5);

	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

3 尾删测试

void TestSeqList3()
{
	SL s;
	SLInit(&s);

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 5);

	SLPrint(&s);

	SLPopBack(&s);
	SLPopBack(&s);
	SLPopBack(&s);

	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

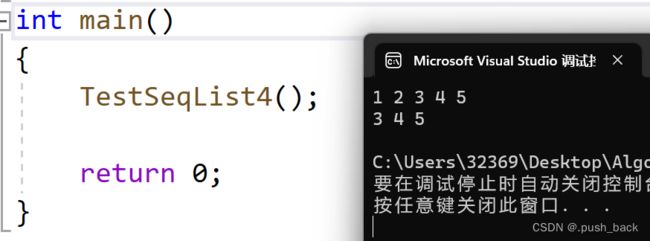
4 头删测试

void TestSeqList4()
{
	SL s;
	SLInit(&s);

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 5);

	SLPrint(&s);

	SLPopFront(&s);
	SLPopFront(&s);

	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

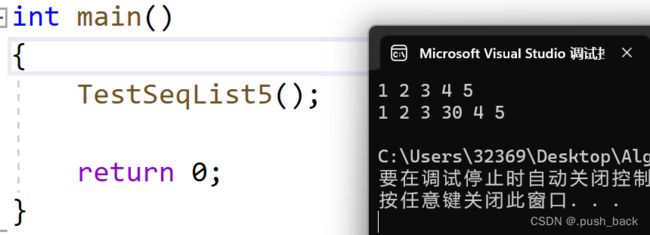
5 插入测试

void TestSeqList5()
{
	SL s;
	SLInit(&s);

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 5);

	SLPrint(&s);

	SLInsert(&s, 3, 30);
	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

6 删除测试

void TestSeqList6()
{
	SL s;
	SLInit(&s);

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 5);

	SLPrint(&s);

	SLErase(&s, 2);
	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

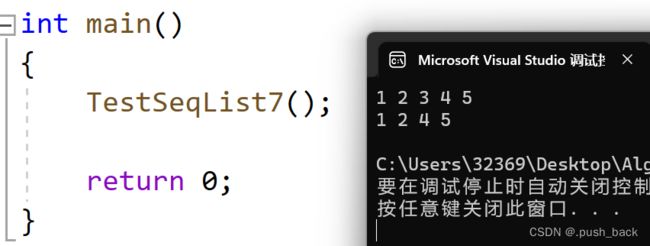
7 查找、修改测试

void TestSeqList7()
{
	SL s;
	SLInit(&s);

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 5);

	SLPrint(&s);

	int pos = SLFind(&s, 3);
	if (pos != -1)
	{
		SLErase(&s, pos);
	}
	SLPrint(&s);

	SLDestroy(&s);
}

运行结果：

题目练习（不定时增加）

1.原地移除数组中所有的元素val。

题目链接：移除元素

方法1：

1. 从前向后遍历数组nums，找到第一个val
2. 将val后面的元素向前移动一位，即删除该val；numsSize-1
3. 循环重复上述操作，直到所有val被删除
4. 返回numSize

时间复杂度：O(n^2) 空间复杂度：O(1)

图解：

代码：

int removeElement(int* nums, int numsSize, int val)
{
    for(int i = 0; i < numsSize; i++) // 遍历数组
    {
        if(nums[i] == val)// 找到val
        {
            for(int j = i;j < numsSize-1; j++)
            {
                nums[j] = nums[j+1];// val后面元素向前移动一位
            }

            i--; // val下一个元素可能也是val，需要重新判断该位置（图解省略了这种情况）
            numsSize--;// 数组个数-1
        }    
    }

    return numsSize;
}

方法2：

1. 设置变量count用来记录数组nums中val的个数
2. 遍历数组，对于数组中每个元素，如果该元素=val则count++，否则将该元素向前移动count个位置（因为前面count个val已经被删除了，后面元素需要向前覆盖）
3. 返回numsSize-count

时间复杂度：O(n) 空间复杂度：O(1)

图解：

代码：

int removeElement(int* nums, int numsSize, int val){
    int count = 0;
    for(int i = 0; i < numsSize; i++)
    {
        if(nums[i] == val)
        {
            count++;
        }
        else
        {
            nums[i-count] = nums[i];
        }
    }


    return numsSize - count;
}

方法3：双指针

1. 用count记录val个数
2. 指针i从前向后扫描数组nums，指针j指向nums[0],如果nums[i]不等于val，则赋值给nums[j]，j指向下一位置，否则，count+1。
3. 返回numsSize-count。

时间复杂度：O(n) 空间复杂度：O(1)

图解：

代码：

int removeElement(int* nums, int numsSize, int val){
    int count = 0;
    for (int i = 0, j = 0; i < numsSize; i++)
    {
        if (nums[i] != val)
        {
            nums[j] = nums[i];
            j++;
        }
        else
        {
            count++;
        }
    }

    return numsSize - count;
}

如果本文内容对你有帮助，可以点赞收藏，感谢支持，期待你的关注。

本专栏下篇预告：单链表实现及练习