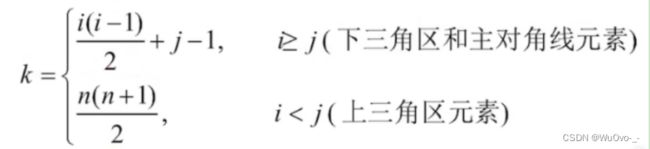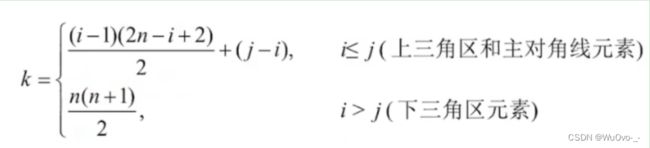数据结构 第三章 栈和队列
目录
一、栈(Stack)
栈
栈的基本概念
栈的基本操作
编辑
栈的常考题型
栈的顺序存储实现
初始化(创):
进栈(增):
出栈(删):
获取栈顶元素(查):
判空、判满
共享栈
栈的链式存储
初始化(创):
进栈(增):
出栈(删):
获取(栈顶元素):
二、队列(Queue)
1.队列
定义:
2.队列顺序存储实现
初始化(创):
入队(增):
出队(删):
获取队头元素(查):
判满、判空
3.队列链式存储实现
初始化
带头节点:
不带头节点:
入队
带头结点:
不带头结点:
出队
带头结点
不带头结点
4.双端队列
5.考点判断输出序列合法性
栈
输入受限的双端队列
输出受限的双端队列
6.栈的应用
栈在括号匹配中的应用
栈在表达求值中的应用(上)
1.中缀转后缀的手算方法
2.后缀表达式的计算(手算)
3.用栈实现后缀表达式的计算
4.中缀转前缀的手算方法
5.用栈实现前缀表达式的计算
6.中缀表达式转后缀表达式(机算)
7.用栈实现中缀表达式的计算
栈在递归中的应用
队列的应用
特殊矩的压缩存储
二维数组的存储结构
普通矩阵的存储
特殊矩阵
2.三角矩阵的压缩存储
3.三对角矩阵的压缩存储
4.稀疏矩阵的压缩存储
第三章 栈和队列
一、栈(Stack)
栈
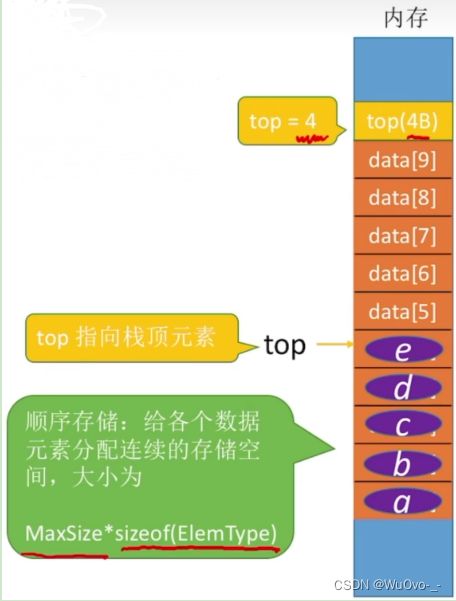
栈的基本概念
栈(Stack)是只允许在一端进行插入或删除操作的线性表
重要术语: 栈顶,栈底,空栈
逻辑结构上:与普通的线性表相同
数据的运算:插入、删除操作有区别,栈只能在栈顶的位置进行相关操作
栈的基本操作
栈的常考题型
考试时不会让你把所有的顺序写出来,一般都是选择题,让你判断某种出栈的顺序是否合法
栈的顺序存储实现
基本操作
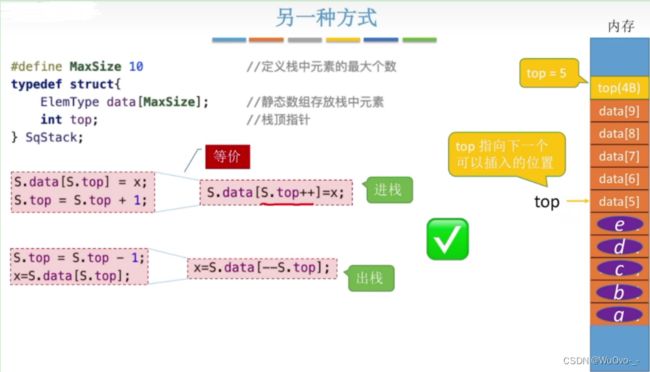
#define MAXSIZE 10
typedef struct
{
int data[MAXSIZE];
int top;//表示栈顶元素的下标
}SqStack;初始化(创):
//--------初始化
void InitSqStack(SqStack* S)
{
(*S).top = -1;//初始化栈顶指针,数组首元素还未赋值,指向0不合理
}进栈(增):
//--------进栈
int Push(SqStack* S,int t)
{
//判满
if ((*S).top == MAXSIZE - 1)
{
return 0;
}
(*S).top += 1;
(*S).data[(*S).top] = t;
//等价于(*S).data[++(*S).top] = t;
return 1;
}出栈(删):
//--------出栈
int Pop(SqStack* S, int s)
{
//判空
if ((*S).top == -1)
{
return 0;
}
s = (*S).data[(*S).top];
(*S).top = (*S).top - 1;
//等价于s = (*S).data[(*S).top--];
return 1;
}被删除的元素还惨留在内存中,只是逻辑上被删除了。
获取栈顶元素(查):
//--------获取栈顶元素
int GetTop(SqStack* S,int* h)
{
//判空
if ((*S).top == -1)
{
return 0;
}
*h = (*S).data[(*S).top];
return 1;
}另一种方式:
判空、判满
//判空
if ((*S).top == -1)
{
return 0;
}//判满
if ((*S).top == MAXSIZE - 1)
{
return 0;
}共享栈
栈的链式存储
链栈的定义:
和单链表的定义几乎没有什么区别,单链表的链头 = 栈顶
typedef struct LinkNode
{
int data;
struct LinkNode* next;
}LNode,*LiStack;初始化(创):
//--------初始化
void InitLiStack(LiStack *S)
{
*S = (LNode*)malloc(sizeof(LNode));
(*(*S)).next = ((void*)0);
}进栈(增):
//--------进栈(单链表的头插)
void Push(LiStack* S)
{
int t = 0;
printf("输入9999退出\n");
scanf("%d", &t);
while (t != 9999)
{
LNode*L = (LNode*)malloc(sizeof(LNode));
(*L).data = t;
(*L).next = (*(*S)).next;
(*(*S)).next = L;
printf("输入9999退出\n");
scanf("%d", &t);
}
}出栈(删):
//--------出栈
void Pop(LiStack* S)
{
LNode* q = (*(*S)).next;
(*(*S)).next =(*q).next;
free(q);
q = NULL;
}获取(栈顶元素):
//获取栈顶元素
int gettop(LiStact* S, int* z)
{
LNode* p = (*(*S)).next;//用指针p指向下一个节点
*z = (*p).data;
/*不用额外定义指针,直接硬套*/
/**z = (* ( (*(*S)).next ) ).data;*/
}二、队列(Queue)
1.队列
定义:
队列(Queue)是只允许在一端进行插入,在另一端进行删除的线性表,队列的插入操作一般称为入队,队列的删除操作一般称为出队。
特点:先进 入队列的元素先 出队
队列的几个术语:队头、队尾、空队列
对头:允许删除的一端
队尾,允许插入的一端
2.队列顺序存储实现
初始化(创):
//--------初始化
void InitQueue(SqQueue* Q)
{
//初始 队头、队尾下标指向0
(*Q).rear = (*Q).front = 0;
}
//--------判空
int QueueEmpty(SqQueue* Q)
{
return ((*Q).rear ==(*Q).front);
}这里注意,rear是指向队尾后一个元素下标,还是就是指向队尾的下标
入队(增):
//--------入队
int EnQueue(SqQueue* Q,int e)
{
//判满条件
//代价:需要牺牲一个空间让rear指向它
if (((*Q).rear + 1) % MAXSIZE == (*Q).front)
{
return 0;//入队失败
}
(*Q).data[(*Q).rear] = e;
(*Q).rear = ((*Q).rear + 1) % MAXSIZE;
return 1;//入队成功
}运用模运算将存储空间在逻辑上变成“环状”
出队(删):
//--------出队
int DeQueue(SqQueue* Q,int* x)
{
//判空
if ((*Q).rear == (*Q).front)
{
return 0;//出队失败
}
(*x) = (*Q).data[(*Q).front];
(*Q).front = ((*Q).front - 1) % MAXSIZE;
return 1;//出队成功
}获取队头元素(查):
//--------查
int DeQueue(SqQueue* Q, int* y)
{
//判空
if ((*Q).rear == (*Q).front)
{
return 0;//查找失败
}
(*y) = (*Q).data[(*Q).front];
return 1;//查找成功
}判满、判空
//判满条件
//代价:需要牺牲一个空间让rear指向它
if (((*Q).rear + 1) % MAXSIZE == (*Q).front)
{
return 0;
}//--------判空
int QueueEmpty(SqQueue* Q)
{
return ((*Q).rear == (*Q).front);
}不浪费存储空间的方法:
方法1:
#define MAXSIZE 10
typedef struct
{
int data[MAXSIZE];//静态数组存放队列元素
int front, rear;//队头下标 和 队尾下标
int size; //当前队列的长度
}SqQueue;插入成功时 size++
删除成功时 size--
判满条件:size == MAXSIZE;
判空条件:size == 0;
方法2:
#define MAXSIZE 10
typedef struct
{
int data[MAXSIZE];//静态数组存放队列元素
int front, rear;//队头下标 和 队尾下标
int tag; //最近进行的是删除/插入 0/1
}SqQueue;插入成功,令tag=1;
删除成功,令tag=0
判满条件:front == rear && tag == 1
判空条件:front == rear && tag == 0
3.队列链式存储实现
typedef struct LinkNode//链式队列 结点
{
int data;
struct LinkNode* next;
}LinkNode;
typedef struct//链式队列
{
LinkNode* front, * rear;
}LinkQueue;初始化
带头节点:
//--------初始化(带头结点)
void InitLinkQueue(LinkQueue* Q)
{
//初始时 front,rear 都指向头结点
(*Q).front = (*Q).rear = (LinkNode*)malloc(sizeof(LinkNode));
(*(*Q).front).next = NULL;
}同时我们可以知道判空的条件
//--------判空(带头结点)
int IsEmpty(LinkQueue* Q)
{
if ((*Q).front == (*Q).rear)
{
return 1;//是空
}
return 0;//不是空
}不带头节点:
//--------初始化(不带头结点)
void InitLinkQueue(LinkQueue* Q)
{
//初始时 front,rear 都指向空
(*Q).front = NULL;
(*Q).rear = NULL;
}同时我们可以知道判空的条件
//--------判空(不带头结点)
int IsEmpty(LinkQueue* Q)
{
if ((*Q).front == NULL)
{
return 1;//是空
}
return 0;//不是空
}入队
带头结点:
//--------入队(带头结点)
void EnQueue(LinkQueue* Q)
{
int t;
printf("请输入数值:>");
scanf("%d", &t);
LinkNode*L = (LinkNode*)malloc(sizeof(LinkNode));
(*L).data = t;
(*L).next = NULL;
(*(*Q).rear).next = L;
(*Q).rear = L;
}不带头结点:
void EnQueue(LinkQueue* Q)
{
int t;
printf("请输入数值:>");
scanf("%d", &t);
LinkNode* S = (LinkNode*)malloc(sizeof(LinkNode));
(*S).data = t;
(*S).next = NULL;
if ((*Q).front == NULL)
{
(*Q).front = S;
(*Q).rear = S;
}
(*(*Q).rear).next = S;
(*Q).rear = S;
}注意要关注rear的操作
出队
带头结点
//--------出队(带头结点)
int DeQueue(LinkQueue* Q,int* x)
{
//判空
if ((*Q).front == (*Q).rear)
{
return 0;//出队失败
}
LinkNode* p = (*(*Q).front).next;
x = (*p).data;
(*(*Q).front).next = (*p).next;
//如果是最后一个结点
if ((*(*Q).front).next == (*Q).rear)
{
(*Q).rear = (*Q).front;
}
free(p);
return 1;
}不带头结点
int DeQueue(LinkQueue* Q, int* x)
{
//判空
if ((*Q).front == NULL)
{
return 0;//出队失败
}
LinkNode* p = (*Q).front;
x = (*p).data;
(*(*Q).front).next = (*p).next;
//如果是最后一个结点
if (p == (*Q).rear)
{
(*Q).rear = (*Q).front = NULL;
}
free(p);
return 1;
}注意要关注front的操作
4.双端队列
双端队列:只允许从两端插入,两端删除的线性表
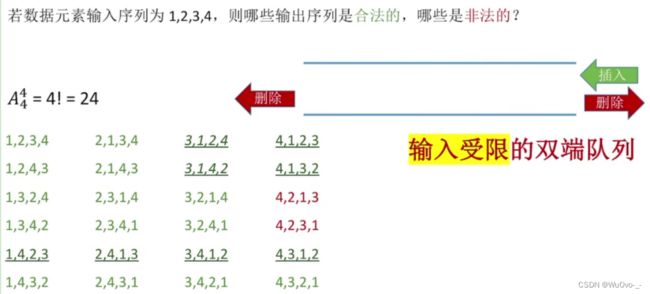
5.考点判断输出序列合法性
栈
输入受限的双端队列
先放到队列里,用删除去拼凑出合法的序列
输出受限的双端队列
先放到队列里,用插入去拼凑出额发的序列
6.栈的应用
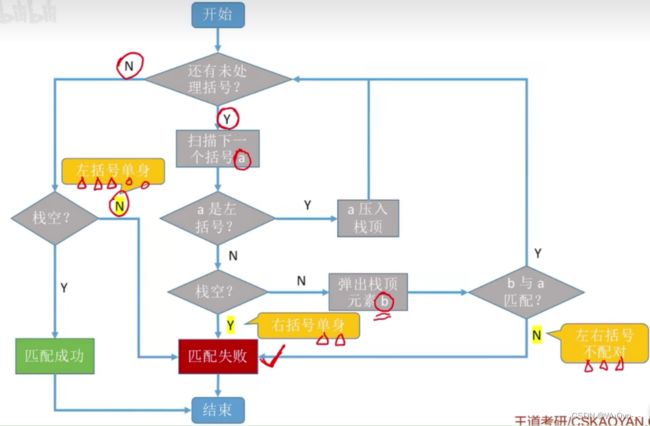
栈在括号匹配中的应用
最后出现的左括号最先被匹配(LIFO),可用‘栈’实现该特性;
每出现一个右括号,就“消耗”一个左括号(出栈)
遇到左括号就入栈;遇到右括号,就“消耗”一个左括号。
栈在表达求值中的应用(上)
三种算数表达式:中缀表达式(运算符在两个操作数中间),后缀表达式(~后面),前缀表达式(~前面)
1.中缀转后缀的手算方法
1,确定中缀表达式中的各个运算符的运算顺序
2. 选择下一运算符,按照左操作数 右操作数 运算符 的方式组合成一个新的操作数
3. 如果还有运算符没被处理,就继续第2步
左优先原则:只要左边的运算符能先计算,就优先算左边的
2.后缀表达式的计算(手算)
从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应的运算,合体为一个操作数
注意两个操作数的左右顺序
3.用栈实现后缀表达式的计算
- 从左往右扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈,并回到第1步;否则执行第3步
- 若扫描到运算符,则弹出两个栈顶元素(注意先出栈的是右操作数),执行相应的运算,运算结果压回栈顶,回到第1步
4.中缀转前缀的手算方法
1.确定中缀表达式中的各个运算符的运算顺序
2. 选择下一运算符,按照左操作数 右操作数 运算符 的方式组合成一个新的操作数
3. 如果还有运算符没被处理,就继续第2步
右优先原则:只要右边的运算符能先计算,就优先算右边的
5.用栈实现前缀表达式的计算
- 从右往左扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈,并回到第1步;否则执行第3步
- 若扫描到运算符,则弹出两个栈顶元素(注意先出栈的是左操作数),执行相应的运算,运算结果压回栈顶,回到第1步
6.中缀表达式转后缀表达式(机算)
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。
从左到右处理各个元素,直到末尾。可能遇到三种情况:
- 遇到操作数。直接加入后缀表达式。
- 遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”不加入后缀表达式。
- 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止。之后再把运算符入栈。
按上述方法处理完毕所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。
7.用栈实现中缀表达式的计算
中缀转后缀 + 后缀表达式的求值 两个算法的结合
初始化两个栈,操作数栈(中缀转后缀)和运算符栈(后缀表达式求和)
若扫描到操作数,压入操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要在弹出两个操作数栈的栈顶元素并执行相应的运算,运算结果再压回到操作数栈顶)
栈在递归中的应用
函数调用的特点:最后被调用的函数最先执行结束 (LIFO)
函数调用时,需要用一个“函数调用栈”存储:
- 调用返回地址
- 实参
- 局部变量
递归调用时,函数调用栈可称为“递归工作栈 ”,
每进入一层递归,就将递归调用所需要信息压入栈顶,
每退出一层递归,就从栈顶弹出相应的信息
缺点:效率低,太多层递归可能会导致栈溢出;可能包含很多重复的运算
队列的应用
- 树的层次遍历
- 图的广度优先遍历
队列在操作系统中的应用
多个进程争抢着使用有限的系统资源时,FCFS(First Come First Service,先来先服务)是一种常用策略
特殊矩的压缩存储
二维数组的存储结构
行优先
列优先
普通矩阵的存储
普通的矩阵可用二维数组进行存储。注意:描述矩阵元素时,行、列号通常从1开始。
特殊矩阵
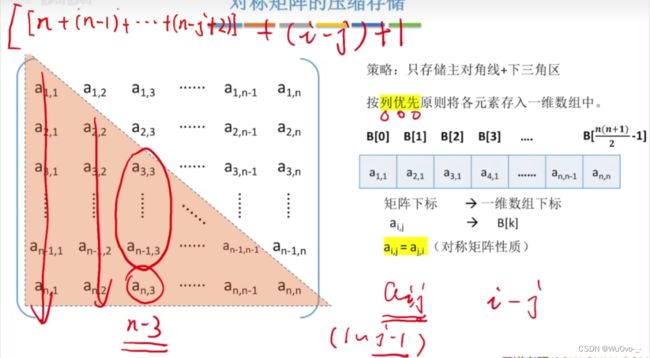
- 对称矩阵的压缩存储
对称矩阵:若n阶方阵中任意一个元素ai,j都有ai,j = ai,j,则该矩阵为对称矩阵
压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区)
策略:只存储主对角线+下三角区 (i >= j)
按行优先原则将各个元素存入一维数组中。
思考:
1.数组大小应是多少?
最后一个元素下标为n(n+1)/2-1
2.站在程序员的角度,对称矩阵压缩存储后怎样才能方便使用?
可以实现一个“映射”函数
矩阵下标 ----> 一维数组下标
Key:按行优先的原则,ai,j是第几个元素?
[1+2+3…+(i-1)]+j ----> 第i(i-1)/2+j个元素(数组是从0开始的还要-1)
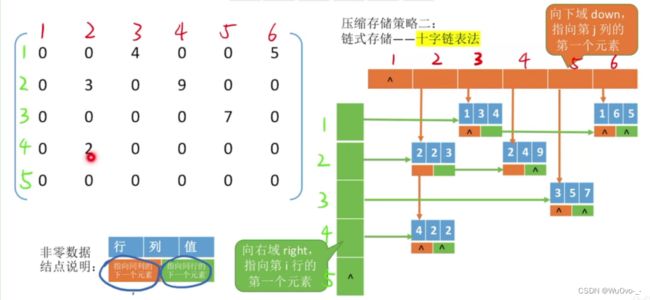
如果要访问上三角区(i 按列优先原则将各个元素存入一维数组中。 下三角矩阵:除了主对角线和下三角区,其余的元素都相同。 压缩存储策略:按行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量c。 上三角矩阵:除了主对角线和上三角区,其余的元素都相同。 三对角矩阵,又称带状存储:当|i-j|>1时,有ai,j = 0(1<=i,j<=n)。 压缩存储策略:按行优先(或列优先)原则,只存储带状部分。 稀疏矩阵:非零元素远远少于矩阵元素的个数。 压缩存储策略 一: 顺序存储 -- 三元组<行、列、值>(一维数组) 压缩存储策略 二: 链式存储 -- 十字链表法2.三角矩阵的压缩存储
3.三对角矩阵的压缩存储
4.稀疏矩阵的压缩存储