有向图计数优化版原理及C++实现
题目
见前面章节。有向图访问计数的原理及C++实现-CSDN博客
第一版
不需要拓扑排序,也不需要并集查找,直接dfs了。完成以下三个职责:
一,DFS那些端点在环上。
二,DFS环上各点此环的长度。
三,DFS非环上各点。
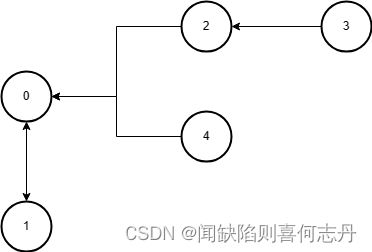
分析
cur是当前dfs的节点,next为edges[cur]。从后向前分析:
判定处理
| ret的值 |
返回值 |
|
| 找到环尾 |
ret [cur] = NO - mPreNO[cur] |
cur |
| 找到环尾,没找到环首 |
ret [cur] = ret [next] |
同dfs(next...) |
| 之前找到环尾和当前环首 |
环尾已处理,无需处理 |
-1 |
| 之前找到首尾 |
ret [cur] = ret [next]+1 |
-1 |
判定表
| 条件一 |
条件二 |
结果 |
| mPreNO.count(cur) |
无 |
找到环尾 |
| dfs(next)返回非-1 |
cur不等于dfs(next) |
找到环尾,没找到环首 |
| cur等于dfs(next) |
之前找到环尾和当前环首 |
|
| dfs(next)返回非-1 |
之前找到首尾 |
| DSF0过程 |
|||
| DFS(0) |
不处理 |
return -1 |
|
| DFS(1) |
ret[1]=2 |
return 0 |
|
| DFS(0) |
ret[0]=3-1=2 |
return 0 |
|
| DFS(1)过程 |
|||
| DFS(1) |
不处理 |
return -1 |
|
| DFS(0) |
ret[0]=2 |
return 0 |
|
| DFS(1) |
ret[1]=3-1=2 |
return 0 |
|
| FFS(2)过程 |
|||
| DFS(2) |
ret[2]=3 |
Return -1 |
|
| DFS(0) |
不处理 |
return -1 |
|
| DFS(1) |
ret[1]=2 |
return 0 |
|
| DFS(0) |
ret[0]=3-1=2 |
return 0 |
|
| FFS(4)过程 |
|||
| DFS(4) |
ret[4]=3 |
Return -1 |
|
| DFS(0) |
不处理 |
return -1 |
|
| DFS(1) |
ret[1]=2 |
return 0 |
|
| DFS(0) |
ret[0]=3-1=2 |
return 0 |
|
| FFS(3)过程 |
|||
| DFS(3) |
Ret[3]=4 |
Return -1; |
|
| DFS(2) |
ret[2]=3 |
Return -1 |
|
| DFS(0) |
不处理 |
return -1 |
|
| DFS(1) |
ret[1]=2 |
return 0 |
|
| DFS(0) |
ret[0]=3-1=2 |
return 0 |
|
核心代码
class Solution {
public:
vector
m_c = edges.size();
m_edges = edges;
m_vRet.assign(m_c, -1);
for (int i = 0; i < m_c; i++)
{
std::unordered_map
dfs(i, mPreNO, 1);
}
return m_vRet;
}
int dfs(int cur,std::unordered_map
{
if (mPreNO.count(cur))
{
m_vRet[cur] = iNO - mPreNO[cur];
return cur;
}
mPreNO[cur] = iNO;
const auto& next = m_edges[cur];
const int iRet = dfs(next, mPreNO, iNO + 1);
if (iRet == cur)
{
return -1;//环结束了
}
if (-1 == iRet)
{
m_vRet[cur] = m_vRet[next]+1;
}
else
{
m_vRet[cur] = m_vRet[next];
}
return iRet;
}
vector
vector
int m_c;
};
记忆化
如果ret[cur]不为-1,说明cur已经处理。如果cur是环上一点,那说明整个环已经处理,返回-1;如果cur,不是环上一点,也返回-1。
时间复杂度
O(n),任意端点,dfs最多执行两次,一次是主动执行,一次是作为出边被执行。
优化后的代码
class Solution {
public:
vector
m_c = edges.size();
m_edges = edges;
m_vRet.assign(m_c, -1);
for (int i = 0; i < m_c; i++)
{
std::unordered_map
dfs(i, mPreNO, 1);
}
return m_vRet;
}
int dfs(int cur,std::unordered_map
{
if (-1 != m_vRet[cur])
{
return -1;
}
if (mPreNO.count(cur))
{
m_vRet[cur] = iNO - mPreNO[cur];
return cur;
}
mPreNO[cur] = iNO;
const auto& next = m_edges[cur];
const int iRet = dfs(next, mPreNO, iNO + 1);
if (iRet == cur)
{
return -1;//环结束了
}
if (-1 == iRet)
{
m_vRet[cur] = m_vRet[next]+1;
}
else
{
m_vRet[cur] = m_vRet[next];
}
return iRet;
}
vector
vector
int m_c;
};
再次优化后的代码
用数组代替哈希映射,速度似乎没提升。
class Solution {
public:
vector
m_c = edges.size();
m_edges = edges;
m_vRet.assign(m_c, -1);
int vPreNO[100000];
for (int i = 0; i < m_c; i++)
{
vPreNO[i] = -1;
}
for (int i = 0; i < m_c; i++)
{
dfs(i, vPreNO, 1);
}
return m_vRet;
}
int dfs(int cur,int* vPreNO,int iNO)
{
if (-1 != m_vRet[cur])
{
return -1;
}
if (-1 != vPreNO [cur])
{
m_vRet[cur] = iNO - vPreNO[cur];
return cur;
}
vPreNO[cur] = iNO;
const auto& next = m_edges[cur];
const int iRet = dfs(next, vPreNO, iNO + 1);
if (iRet == cur)
{
return -1;//环结束了
}
if (-1 == iRet)
{
m_vRet[cur] = m_vRet[next]+1;
}
else
{
m_vRet[cur] = m_vRet[next];
}
return iRet;
}
vector
vector
int m_c;
};
注意
如果用vector
测试环境
VS2022 Win10 C++17
下载
源码下载:
【免费】.有向图计数优化版原理及C++实现资源-CSDN文库
doc文档下载:
【免费】闻缺陷则喜之算法册C++实现资源-CSDN文库