经典算法-----迷宫问题（栈的应用）

目录

前言

迷宫问题

算法思路

1.栈的使用方法 

​编辑2.方向的定义

代码实现

栈的cpp代码：

栈的头文件h代码:

走迷宫代码：

---

前言

        今天学习一种算法问题，也就是我们常见的迷宫问题，本期我们通过前面学习过的数据结构---栈来去完美的解决这个问题，下面看问题！

迷宫问题

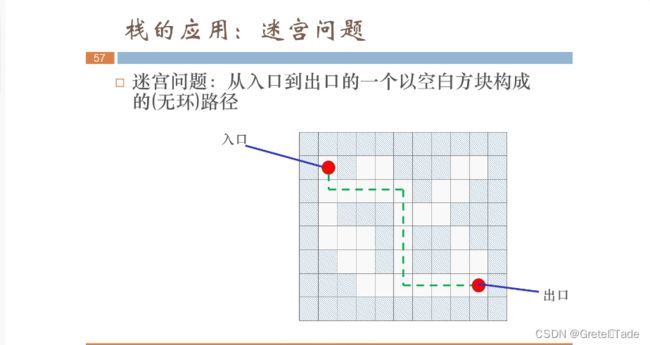
        给定一个迷宫，指明起点和终点，找出从起点出发到终点的有效可行路径，就是迷宫问题（maze problem）。

迷宫可以以二维数组来存储表示。0表示通路，1表示障碍。注意这里规定移动可以从上、下、左、右四方方向移动

int maze[6][6] = {
		{1,1,1,1,1,1},
		{1,0,0,1,1,1},
		{1,0,0,0,0,0},
		{1,0,1,1,1,0},
		{1,0,0,0,0,1},
		{1,1,1,1,1,1}
	};

算法思路

1.栈的使用方法 

        迷宫问题，二维数组外围全是1的围墙，在里面规定一个起始地点和终点，这里我们要想找到起点到终点的路径，就需要一个数据结构去储存这个路径，这里可以用到栈的后进先出的特点，每次进入到一个可通过的点，就把这个点存入到栈当中，直到遇到了死胡同的时候，就回到上一个点，这时候就进行出栈的操作，然后走另外一条路，直到走到终点为止。

2.方向的定义

了解了栈的使用方法，那这里就要去定义移动的方向了，当走到某一个点的时候就要考虑优先往那边走，这时候可以根据迷宫的入口和出口大致方向去决定优先方向，这里的迷宫入口在出口的西北方向，那么优先的方向我依次为东、南、西、北，也就是说优先往东走，其次是南、西、北。方向的移动可以根据当前坐标进行上下左右的移动，只需要去定义一个方向数组，然后加上这个数组的方向即可。

 方向的储存结构：

//试探方向存储结构
typedef struct {
	int xx, yy;
}Direction;
//东南西北
Direction dire[4] = { {0,1},{1,0},{0,-1},{-1,0} };

代码实现

栈的cpp代码：

#include
#include

//数据类型
typedef struct datatype {
	int x, y, di;
}ElemType;
//节点
typedef struct node {
	ElemType data;
	struct node* next;
}Node;
//栈顶指示
typedef struct stack {
	int count;	//计数
	Node* point;
}Stack;


//创建节点
Node* create_node(ElemType data) {
	Node* new_node = (Node*)malloc(sizeof(Node));
	if (new_node) {
		new_node->data = data;
		new_node->next = NULL;
		return new_node;
	}
	else
	{
		printf("ERROR\n");
	}
}

//初始化
void stack_init(Stack* top) {
	top->count = 0;
	top->point = NULL;
}

int isEmpty(Stack* top) {
	if (top->count == 0) {
		return 1;
	}
	return 0;
}


//入栈
void push(Stack* top, ElemType data) {
	Node* new_node = create_node(data);
	if (new_node) {
		top->count++;
		if (top->count == 1) {//如果入栈是第一个节点的话
			top->point = new_node;
		}
		else
		{
			new_node->next = top->point;
			top->point = new_node;
		}
	}
	else
		return;
}


//出栈
Node* pop(Stack* top) {
	Node* pop_node = NULL;
	if (!isEmpty(top)) {
		pop_node = top->point;
		top->point = pop_node->next;
		top->count--;
	}
	return pop_node;
}


//递归输出路径
void show_path(Node* node) {
	if (!node)
		return;
	show_path(node->next);
	printf("(%d,%d)\n", node->data.x, node->data.y);
}

栈的头文件h代码:

#pragma once
//链表栈
//数据类型
typedef struct datatype {
	int x, y, di;
}ElemType;
//节点
typedef struct node {
	ElemType data;
	struct node* next;
}Node;
//栈顶指示
typedef struct stack {
	int count;	//计数
	Node* point;
}Stack;


void stack_init(Stack* top);
int isEmpty(Stack* top);
void push(Stack* top, ElemType data);
Node* pop(Stack* top);
void show_path(Node* node);

走迷宫代码：

#include
#include
#include"stack.h"

//试探方向存储结构
typedef struct {
	int xx, yy;
}Direction;
//东南西北
Direction dire[4] = { {0,1},{1,0},{0,-1},{-1,0} };

//判断能不能走出去,路径放入到了栈里面去
bool Findpath(int maze[][6],Stack* stack ,Direction dir[],int startx,int starty,int endx,int endy) {
	//startx,starty是起点的坐标;endx、endy是终点的坐标.
	assert(stack);
	int x, y, di;
	int line, col;
	//初始化
	maze[startx][starty] = -1;
	ElemType start = { startx,starty,-1 };
	push(stack, start);

	while (!isEmpty(stack)) {
		Node* po = pop(stack);
		ElemType temp = po->data;
		x = temp.x;
		y = temp.y;
		di = temp.di++;
		//使得栈储存了一条通路
		while (di < 4) {
			line = x + dire[di].xx;
			col = y + dire[di].yy;
			if (maze[line][col] == 0) {
				//储存上一个节点的位置，入栈
				temp = { x,y,di };
				push(stack, temp);
				x = line;
				y = col;
				maze[line][col] = -1;
				if (x == endx && y == endy) {
					//把终点的位置入栈
					temp = { x,y,-1 };
					push(stack, temp);
					return true;
				}
				else
					di = 0;
			}
			else
				di++;
		}
	}
	return false;
}



int main() {
	int maze[6][6] = {
		{1,1,1,1,1,1},
		{1,0,0,1,1,1},
		{1,0,0,0,0,0},
		{1,0,1,1,1,0},
		{1,0,0,0,0,1},
		{1,1,1,1,1,1}
	};
	Stack stack;
	stack_init(&stack);
	printf("能否出去：%d\n", Findpath(maze, &stack, dire, 1, 1, 4, 4));
	show_path(stack.point);//输出遍历的结果
}

输出结果：

好了，以上就是本期的全部内容了，我们下次见咯！

分享一张壁纸：