插入排序的3种实现方式（包含希尔排序）

插入排序的基本方法是：每一步将一个待排序的元素，按其排序码的大小，插入到前面已经排好序的一组元素的适当位置上去，直到元素全部插入为止。

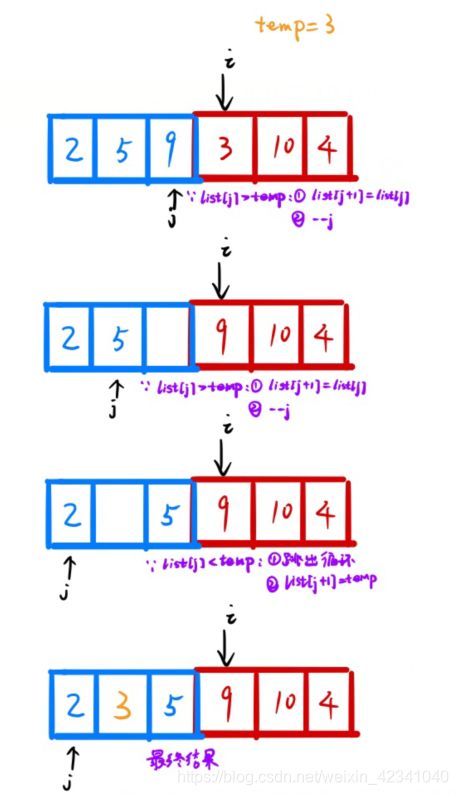
顺序法定位插入位置——直接插入排序

i表示当前要排序的元素，j是i的前面一个元素。
1.复制插入的元素：

temp = list[i];

2.记录后移，查找插入的位置

for (; j >= 0 && list[j] > temp; --j) 
			list[j + 1] = list[j];

3.插入到正确的位置

list[j + 1] = temp;

#include
#include 
using namespace std;
vector<int> insertSort(vector<int>list) {
	if (list.empty())
		return list;
	int i, j, temp;
	for (i = 1; i < list.size(); ++i) {//从第二个数开始遍历
		temp = list[i];
		j = i - 1;
		for (; j >= 0 && list[j] > temp; --j) {
			list[j + 1] = list[j];
		}
		list[j + 1] = temp;
	}
	return list;
}
int main() {
	vector<int>list{ 8,2,1,7,4,9,3,6,5 };
	auto res = insertSort(list);
	for (auto& item : res)
		cout << item << " ";
	//1 2 3 4 5 6 7 8 9
}

最好的情况（初始状态全部是按顺序排）

比较的次数：${\sum }_{i=1}^{n-1}1=n-1$;
移动的次数：0

最坏的情况（初始状态全部是逆序排）

比较的次数：${\sum }_{i=1}^{n-1}i=(n-1)n÷2$;
移动的次数：${\sum }_{i=1}^{n-1}(i+2)=(n-1)(n+4)÷2$

平均的情况

比较的次数：${\sum }_{i=1}^{n-1}(i+1)/2=(n-1)(n+2)÷4$;
移动的次数：${\sum }_{i=1}^{n-1}((i+1)/2+1)=(n-1)(n+6)÷4$

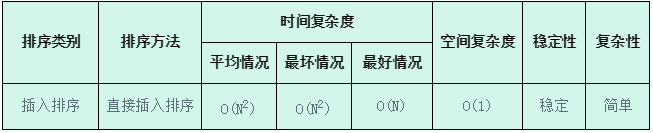
复杂度

二分法定位插入位置——二分插入法

折半插入排序的对象移动次数与直接插入排序相同，依赖于对象的初始排列。
1.减少了比较次数，但没有减少移动次数；
2.但是平均性能优于直接插入排序。
二分法所需要的比较次数与待排序对象的初始排列无关，仅仅依赖于对象个数n。在插入第i个元素时，需要经过$lo{g}_{2}i$次比较，才能确定它应该插入的位置。
1.当n比较大时，用二分法比直接插入排序的最坏情况要好得多，但比它的最好情况要差;
2.当初始队列已经排好序或者接近排好，直接插入排序比折半插入排序的比较次数要少。

#include
#include 
using namespace std;
vector<int> BinsertSort(vector<int>list) {
	int i, j, temp, mid;     
	int low, high;     
	for (i = 1; i < list.size(); i++)
	{
		temp = list[i];
		low = 0;      
		high = i - 1;  
		while (low <= high) {
			mid = (low + high) / 2;
			if (temp < list[mid])//temp <= list[mid]会影响稳定性
				high = mid - 1;
			else
				low = mid + 1;
		}
		/*确定好位置后，将位置之后的数据后移，插入待排序数据*/
		for (j = i - 1; j > high; j--)
		{
			list[j + 1] = list[j];
		}
		list[high + 1] = temp;
	}
	return list;
}

int main() {
	vector<int>list{ 8,2,1,7,4,9,3,6,5 };
	auto res = BinsertSort(list);
	for (auto& item : res)
		cout << item << " ";
	//1 2 3 4 5 6 7 8 9
}

时间复杂度

折半插入排序减少了比较元素的次数，约为O(nlogn)，比较的次数取决于表的元素个数n。但是移动次数不变，因此，折半插入排序的时间复杂度仍然为O(n²)，但它的效果还是比直接插入排序要好。
最坏情况(完全逆序)：$O(n^2)$
最好情况(已经排好)：$O(nlogn)$
平均情况：$O(n^2)$，在 n较大时会减少元素比较的次数，但元素移动次数不变，故仍为$O(n^2)$

空间复杂度

排序只需要一个位置来暂存元素$O(1)$

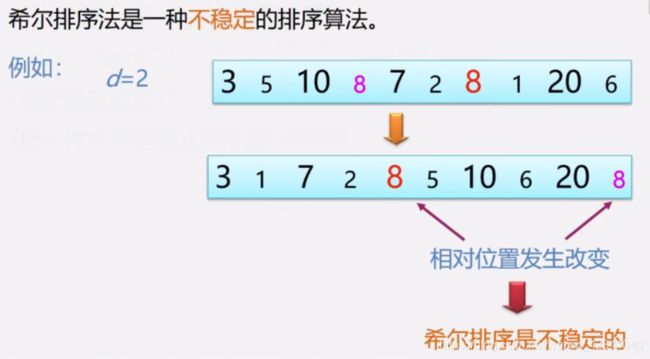
稳定性

• 稳定

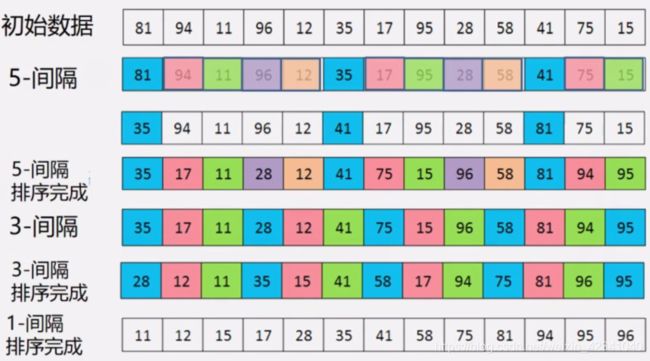
缩小增量多遍插入排序——希尔排序

出发点：增大步幅来提升直接插入排序的效率。
先将整个待排序列分割成若干子序列，分别进行直接插入排序，待整个序列中的记录”基本有序“时，再对全体记录进行一次直接插入。
特点：
1）缩小增量，增量序列必须是递减的，最后一个必须是1；
2）增量序列应该是互质的（序列内元素之间最大公约数为1）；
3）最后一次只需要少量移动

#include
#include 
using namespace std;
vector<int> shellsort(vector<int> a)
{
	int n = a.size();
	int i, gap, temp, j;
	for (gap = n / 2; gap > 0; gap /= 2)//gap最后一次进入循环保证为1
		for (i = gap; i < n; i++)//从数组第gap个元素开始  
			if (a[i] < a[i - gap])//每个元素与自己组内的数据进行直接插入排序  
			{
				temp = a[i];//存起来
				j = i - gap;//j不再是i-1，而是i-gap
				for (; j >= 0 && a[j] > temp; j -= gap) {
					a[j + gap] = a[j];
				}
				a[j + gap] = temp;//不是j+1而是j+gap
			}
	return a;
}

int main() {
	vector<int>list{ 8,2,1,7,4,9,3,6,5 };
	auto res = shellsort(list);
	for (auto& item : res)
		cout << item << " ";
	//1 2 3 4 5 6 7 8 9
}

时间复杂度

和增量序列有关
最好情况：$O(n)$
最坏情况：$O(n^2)$
平均情况：大约$O(n^{1.3})$

空间复杂度

$O(1)$

稳定性

总结