java实现七种经典排序算法
简单算法:冒泡,简单选择,直接插入
改进算法:希尔,堆,归并,快速
直接插入排序:将一个记录插入到已经拍好的有序列表中,从而得到一个新的、记录数增加1的有序表。
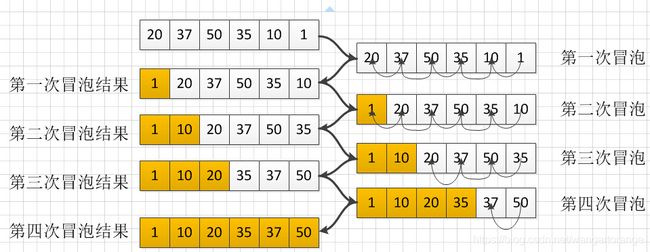
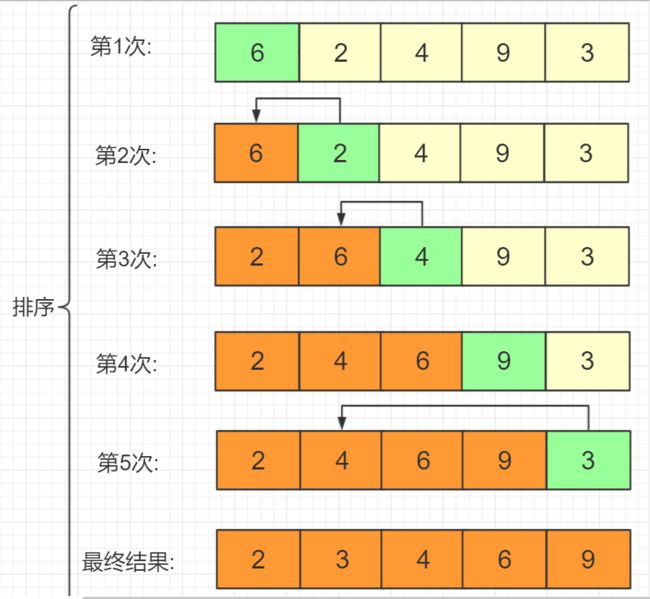
冒泡排序:两两比较,反序交换。每趟将最大(小 )的浮到最上面或沉到最底下。
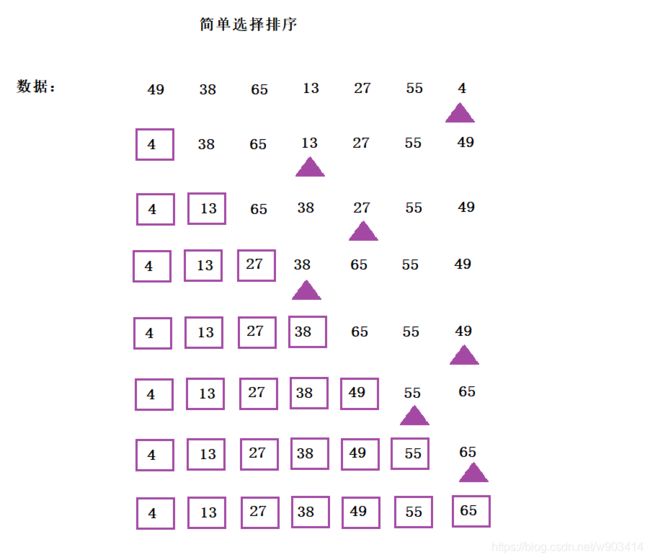
简单选择排序:通过关键字之间的比较,每次将剩余的记录中选择最小的与指定位置交换。
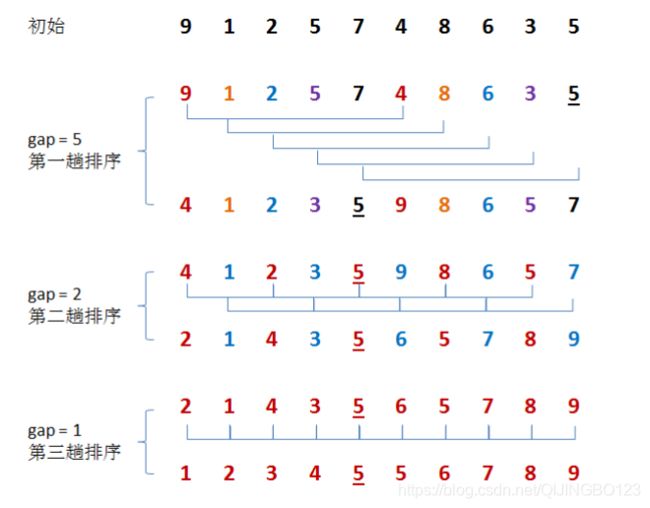
希尔排序:跳跃的插入排序,选择某个增量,对间隔增量的子序列进行排序,随着增量递减,逐步完成所有值的排序。
堆排序:将待排序序列构建成一个大顶堆,此时整个序列最大值就是根节点。将它和末尾元素交换,随后将剩余的n-1个元素重新构造成一个堆,以此类推。
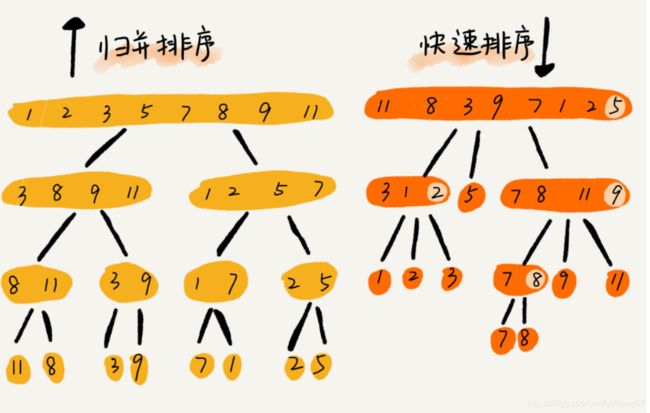
归并排序:拆分,随后重组。
快速排序:通过一趟排序将待排记录分成独立的两部分,一部分都小于另一部分,随后对两部分分别进行再次排序,以达到整体有序。
(所有代码均可独立运行成功)
冒泡排序:
import java.util.Arrays;
/**
* 冒泡排序算法
* 两两比较相邻记录的关键字,如果反序则交换,直到没有反序记录为止
* @author 诸葛浪
*
*/
public class BubbleSortDemo {
public static void bubbleSort0(int[] arr) {
//初级版本冒泡算法 每一个关键字都和后面每一个关键字相比较
for(int i =0;i arr[j])
swap(arr, i, j);
}
public static void bubbleSort(int[] arr) {
//从后往前 两两比较 每一轮把最小的转移到i的位置
for(int i=0;ii;j--)//for(int j=0 ; j arr[j])
swap(arr, j-1, j);
}
public static void bubbleSort2(int[] arr) {
//改进版 如果一趟下来没有交换 说明有序 之后就不必循环判断了
boolean flag = true;//用以记录是否发生交换
for(int i = 0;ii;j--) {
if(arr[j-1] > arr[j]) {
swap(arr, j-1, j);
flag = true;
}
}
}
}
public static void main(String[] args) {
int[] arrTest = {9,1,5,8,3,7,4,6,2};
System.out.println("before: " + Arrays.toString(arrTest));
bubbleSort2(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
public static void swap(int[] arr , int i, int j) {
//交换数组两元素
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
直接插入排序:
import java.util.Arrays;
/**
* 插入排序算法
* 基本操作是将一个记录插入到已经排好序的有序表中,从而得到一个记录数+1的有序表
* @author 诸葛浪
*
*/
public class InsertSortDemo {
public static void insertSort(int[] arr) {
//设置一个辅助空间arr[0]
for(int i =2;i arr[0];j--)
arr[j+1] = arr[j];//记录后移
arr[j+1] = arr[0];//插入到正确位置
}
}
}
public static void main(String[] args) {
int[] arrTest = {0,1,5,8,3,7,4,6,2};
System.out.println("before: " + Arrays.toString(arrTest));
insertSort(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
} 简单选择排序
import java.util.Arrays;
/**
* 简单选择排序
* 基本思想是每一趟在n-i个记录中选择最小的作为第i个记录(从0开始)
*
* @author 诸葛浪
*
*/
public class SelectSortDemo {
public static void selectSort(int[] arr) {
//选择排序 每一趟找到最小的放到i的位置
for(int i=0;i arr[j] )//如果有小于当前最小值的关键字
min = j; //将此下标赋值给min
}
if(i != min)//有更改 则交换
swap(arr, i, min);
}
}
public static void main(String[] args) {
int[] arrTest = {9,1,5,8,3,7,4,6,2};
System.out.println("before: " + Arrays.toString(arrTest));
selectSort(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
public static void swap(int[] arr , int i, int j) {
//交换数组两元素
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
} 希尔排序:
import java.util.Arrays;
/**
* 希尔排序 又叫增量递减排序
* 将相距某个”增量“的记录组成一个子序列
* 保证在子序列内分别进行直接插入排序后得到的结果是基本有序的
* 直接插入排序的升级版
* @author 诸葛浪
*
*/
public class ShellSortDemo {
public static void shellSort(int[] arr) {
//增量递减的插入排序
int increment = arr.length;
do {
increment = increment / 3 + 1;
for(int i = increment + 1 ; i < arr.length; i++) {
if(arr[i] < arr[i - increment]) {//对间隔增量的位置进行比较
arr[0] = arr[i];//暂存在0
int j;
for(j = i - increment; j> 0 && arr[0] < arr[j]; j -= increment)
arr[j+increment] = arr[j];//记录后移 查找插入位置
arr[j+increment] = arr[0];
}
}
}while(increment > 1);
}
public static void main(String[] args) {
int[] arrTest = {0,1,5,8,3,7,4,6,2};
System.out.println("before: " + Arrays.toString(arrTest));
shellSort(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
}
堆排序:
import java.util.Arrays;
/**
* 堆排序 利用完全二叉树的结构
* 对于完全二叉树来说,层序遍历之后如果i>1 则i/2(向上取整3.5->3)为其双亲节点
* 而双亲节点均大于或小于子节点
* 根节点最大称大顶堆 否则小顶堆
* 通过不断移除根节点(与末尾结点交换)并重新组织成堆
* 从而得到有序序列
* 简单选择排序的升级版
* @author 诸葛浪
*
*/
public class HeapSortDemo {
public static void heapSort(int[] arr) {
for(int i = (arr.length-1)/2; i>0;i--)
heapAdjust(arr, i, arr.length-1);
for(int i = (arr.length-1);i>1;i--) {
swap(arr, 1, i);
heapAdjust(arr, 1, i-1);
}
}
public static void heapAdjust(int[] arr, int s, int m) {
//将s到m调整为大顶堆
int temp = arr[s];
for(int j = s*2;j<=m;j*=2) {//左孩子节点2*s 右孩子2*s+1
if(j < m && arr[j] < arr[j+1])//左孩子小于右孩子 j指向右孩子
++j;
if(temp >= arr[j])//根节点大于右孩子 满足大顶堆特性 跳出循环
break;
arr[s] = arr[j];//否则将大节点赋值给根节点
s = j;//根节点向下指向孩子节点
}
arr[s] = temp;
}
public static void swap(int[] arr , int first, int next) {
//交换数组两元素
int temp = arr[first];
arr[first] = arr[next];
arr[next] = temp;
}
public static void main(String[] args) {
int[] arrTest = {0,50,10,90,30,70,40,80,60,20};
System.out.println("before: " + Arrays.toString(arrTest));
heapSort(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
}
归并排序:
import java.util.Arrays;
/**
* 归并排序算法
* 假设初始序列含有n个记录 则可以看成是n个有序的子序列 每个子序列长度为1
* 然后两两归并 得到n/2(向上取整)个长度为2或1的有序子序列 两两归并 如此重复
* 直到得到长度为n的有序序列为止 称为2路归并
* 一种拆分到最小 并从最小合并成最大的思路
* 拆分之后的归并实际上是选择排序的一种
* @author 诸葛浪
*
*/
public class MergeSortDemo {
public static void mergeSort(int[] arr ) {
mSort(arr, arr, 0, arr.length-1);
}
public static void mSort(int[] SR,int[] TR1,int s, int t ) {
int m;
int[] TR2 = new int[SR.length + 1];
if(s == t)//递归返回条件 拆分至最小了
TR1[s] = SR[s];
else {
m = (s+t)/2; //将SR[s..t]分成s到m和m+1到t
mSort(SR, TR2, s, m); //递归地将SR[s...m]归并为有序的TR2[s..m]
mSort(SR, TR2, m+1, t); //同上
merge(TR2,TR1,s,m,t);//TR2归并到TR1中
}
}
public static void merge(int[] SR,int[] TR,int i, int m ,int n ) {
//将有序的SR[i..m]和SR[m+1...n]归并为有序的TR[i...n]
int j,k,l;
for(j = m+1,k=i;i<=m&&j<=n;k++) {//两半里面挨个挑 将SR中记录由小到大并入TR
if(SR[i] < SR[j])//比较符号反过来就是从大到小的排序
TR[k] = SR[i++];
else
TR[k] = SR[j++];
}
//剩下哪个全都归入TR数组
if(i <= m)
for(l = 0;l<=m-i;l++)
TR[k+l] = SR[i+l];
if(j <= n)
for(l = 0;l<=n-j;l++)
TR[k+l] = SR[j+l];
}
public static void main(String[] args) {
int[] arrTest = {50,10,90,30,70,40,80,60,20};
System.out.println("before: " + Arrays.toString(arrTest));
mergeSort(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
}快速排序:
import java.util.Arrays;
/**
* 快速排序算法
* 属于交换排序
* 基本思想是通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分小
* 则可以分别对这两个部分继续进行排序 以达到整个序列有序的目的
*
* @author 诸葛浪
*
*/
public class QuickSortDemo {
public static void quickSort(int[] arr) {
qSort(arr, 0, arr.length-1);
}
/*对arr中的子序列arr[low...high]做快速排序*/
public static void qSort(int[] arr, int low,int high) {
int pivot;//枢轴变量
if(low < high) {
//将arr[]一分为二 算出枢轴值pivot
//pivot = partition(arr, low ,high);
pivot = partition1(arr, low, high);
qSort(arr, low, pivot-1);//对低子表进行递归排序
qSort(arr, pivot+1, high);//对高子表进行递归排序
}
}
/*交换arr中字表的记录 使枢轴记录到位 并返回其所在位置,此时在它之前均不大于他 之后均不小于他*/
public static int partition(int[] arr, int low, int high) {
int pivotKey = arr[low];//用子表的第一个记录作为枢轴值
while(low < high) {//low和high双指针不断向中间靠拢,枢轴值也在不断移动 性能依赖枢轴值在序列中的分布
//另一个版本中也可以不移动枢轴值 最后赋值皆可
while(low < high && arr[high] >= pivotKey)
high--;
swap(arr, low, high);
while(low < high && arr[low] <= pivotKey)
low++;
swap(arr, low, high);
}
return low;
}
public static int partition1(int[] arr, int low, int high) {
int pivotKey ;//用子表三数取中法 作为枢轴值
int m = low +(high - low) /2;//找到序列中间位置
if(arr[low] > arr[high])
swap(arr, low, high);
if(arr[m] > arr[high])
swap(arr, high, m);
if(arr[m] > arr[low])
swap(arr, m, low);
pivotKey = arr[low];//此时枢轴值选择为左中右三个数中位数值
while(low < high) {
//可以不移动枢轴值 最后赋值皆可
while(low < high && arr[high] >= pivotKey)
high--;
arr[low] = arr[high]; //改为直接赋值
while(low < high && arr[low] <= pivotKey)
low++;
arr[high] = arr[low];
}
arr[low] = pivotKey;
return low;
}
public static void swap(int[] arr , int i, int j) {
//交换数组两元素
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arrTest = {50,10,90,30,70,40,80,60,20};
System.out.println("before: " + Arrays.toString(arrTest));
quickSort(arrTest);
System.out.println("after: " + Arrays.toString(arrTest));
}
}
快排和归并的示意图:
再加一个啊哈磊的图