八大排序（三）堆排序，计数排序，归并排序

一、堆排序

什么是堆排序：堆排序（Heap Sort）就是对直接选择排序的一种改进。此话怎讲呢？直接选择排序在待排序的n个数中进行n-1次比较选出最大或者最小的，但是在选出最大或者最小的数后，并没有对原来的序列进行改变，这使得下一次选数时还需要对全部数据进行比较，效率大大降低。

堆排序的原理：

1. 将待排序序列构造成一个大顶堆
2. 此时，整个序列的最大值就是堆顶的根节点。
3. 将其与末尾元素进行交换，此时末尾就为最大值。
4. 然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

如果读到这里，对堆的一些概念不懂得可以翻阅我的另一篇博客“数据结构——【堆】_#欲速则不达#的博客-CSDN博客”，这里面有更详细的堆概念介绍。

代码实现：

#include
//交换函数
void Swap(int* p1, int* p2)
{
	int temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}
//向下调整
void down(int*a,int n,int parent)
{
	//大堆
	int child = parent * 2 + 1;
	//大堆
	while (child  child + 1)
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
}


int main()
{
	//排序该数组
	int arr[] = { 5,9,2,6,0,4,8,1,3,7 };
	//建大堆
	for (int i = 4; i >=0; i--)
	{
		down(arr, 10, i);
	}
	//将数组再次插入其中
	int end = 10 - 1;
	while (end > 0)
	{
		Swap(&arr[0], &arr[end]);
		down(arr, end, 0);
		end--;
	}
	//打印
	for (int i = 0; i < 10; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

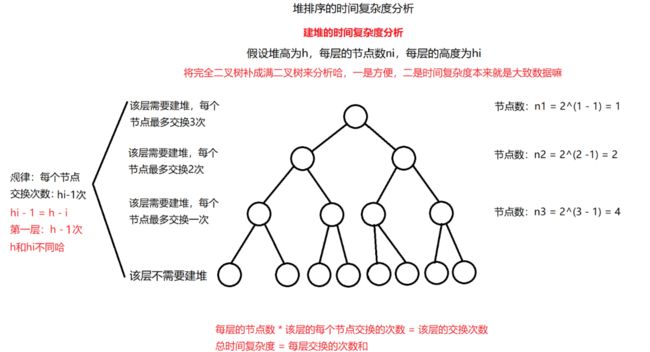
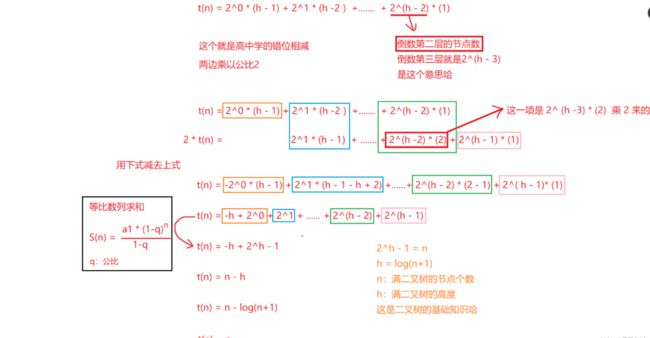
时间复杂度：

二、计数排序

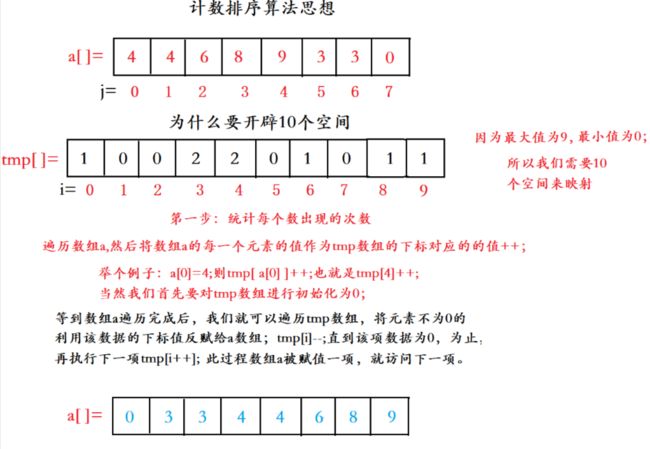
计数排序思路：

1. 根据待排序集合中最大元素和最小元素的差值范围，申请额外空间；
2. 遍历待排序集合，将每一个元素出现的次数记录到元素值对应的额外空间内；
3. 对额外空间内数据进行计算，得出每一个元素的正确位置；
4. 将待排序集合每一个元素移动到计算得出的正确位置上。

代码实现：

#include
#include
#include

void CountSort(int* a, int n)
{
	int min = a[0];
	int max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	printf("range=%d \n", range);
	if (count == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	memset(count, 0,sizeof(int) * range);
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	//排序
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}
int main()
{
	int arr[] = { 4,8,4,3,2,0,9,1,6,8,3,21,7,4,2,1,6,8 };
	int len = sizeof(arr) / sizeof(int);
	CountSort(arr, len);
	for (int i = 0; i < len; i++)
	{
		printf("%d ",arr[i] );
	}
	return 0;
}

时间复杂度：

平均时间复杂度：Ο(n+k)

空间复杂度：Ο(n+k)

三、归并排序

归并排序思路：

归并排序算法有两个基本的操作，一个是分，也就是把原数组划分成两个子数组的过程。另一个是治，它将两个有序数组合并成一个更大的有序数组。

将待排序的线性表不断地切分成若干个子表，直到每个子表只包含一个元素，这时，可以认为只包含一个元素的子表是有序表。
将子表两两合并，每合并一次，就会产生一个新的且更长的有序表，重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表。

代码实现： 

#include
#include
#include
void _MergeSort(int* a, int* tmp, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int mid = (begin + end) / 2;
	//分为左右两块
	//左
	_MergeSort(a, tmp, begin, mid);
	//右
	_MergeSort(a, tmp, mid+1, end);

	int begin1 = begin;
	int begin2 = mid+1;
	int end1 = mid;
	int end2 = end;

	int index = begin;

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}


	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}

	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	_MergeSort(a, tmp, 0, n - 1);

	free(tmp);
}

/// ///
//归并排序非递归

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			// [begin1,end1] [begin2,end2] 归并
			if (begin2 >= n)
			{
				break;
			}

			// 如果第二组的右边界越界，修正一下
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}

			// 拷贝回原数组
			memcpy(a + i, tmp + i, (end2-i+1) * sizeof(int));
		}
		gap *= 2;
	}

	free(tmp);
}

void Print(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}
int main()
{
	int arr[] = { 2,5,7,9,1,0,3,4,6,8,10};
	int len = sizeof(arr) / sizeof(int);
	MergeSortNonR(arr, len);
	Print(arr, len);
	return 0;
}

时间复杂度：

归并排序方法就是把一组n个数的序列，折半分为两个序列，然后再将这两个序列再分，一直分下去，直到分为n个长度为1的序列。然后两两按大小归并。如此反复，直到最后形成包含n个数的一个数组。

归并排序总时间 = 分解时间 + 子序列排好序时间 + 合并时间

无论每个序列有多少数都是折中分解，所以分解时间是个常数，可以忽略不计，则：

归并排序总时间 = 子序列排好序时间 + 合并时间

假设处理的数据规模大小为 n，运行时间设为：T(n)，则T(n) = n，当 n = 1时，T(1) = 1

由于在合并时，两个子序列已经排好序，所以在合并的时候只需要 if 判断即可，所以n个数比较，合并的时间复杂度为 n。

将 n 个数的序列，分为两个 n/2 的序列，则：T(n) = 2T(n/2) + n
将 n/2 个数的序列，分为四个 n/4 的序列，则：T(n) = 4T(n/4) + 2n
将 n/4 个数的序列，分为八个 n/8 的序列，则：T(n) = 8T(n/8) + 3n
…
将 n/2k 个数的序列，分为2k个 n/2k 的序列，则：T(n) = 2kT(n/2k) + kn
当 T(n/2k) = T(1)时， 即n/2k = 1（此时也是把n分解到只有1个数据的时候），转换为以2为底n的对数：k = log2n，把k带入到T(n)中，得：T(n) = n + nlog2n。

使用大O表示法，去掉常数项 n，省略底数 2，则归并排序的时间复杂度为：O(nlogn)

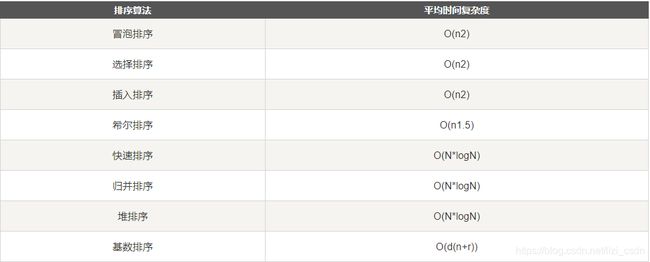
四、八大排序的复杂度和稳定性

稳定排序有：插入排序、冒泡排序、归并排序
不稳定排序：希尔排序、快速排序、选择排序、堆排序
口诀，不稳定的排序：快（快排）些（希尔）选（选择）一堆（堆排）