算法笔记学习（3）---深度优先搜索（DFS）

深度优先搜索（DFS）

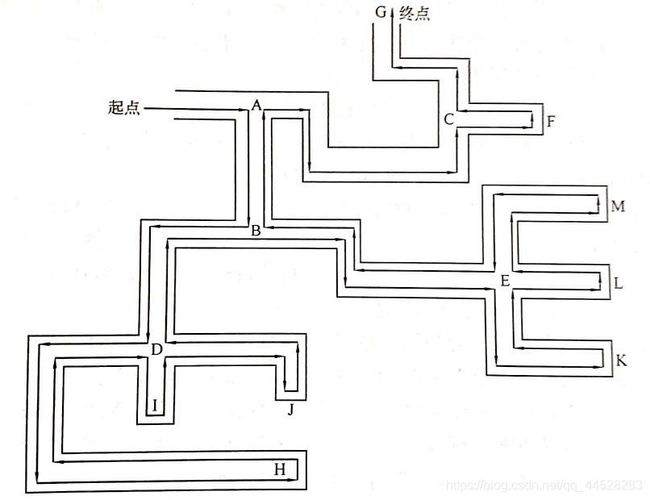
设想我们现在身处一个巨大的迷宫之中，以当前所在位置为起点，沿着一条路向前走，当碰到岔路口的时候，就选择其中一个岔道口前进。如果选择的这个岔路前方是一条死路，就退回到这个岔道口，选择另一个岔路前进。如果岔路中存在新的岔道口，那么依然按上面的方法枚举新岔道口的每一条岔路。这样，只要迷宫存在出口，那么这个方法一定能够找到它。

下面举一个迷宫的例子，分步骤解释如何通过DFS找到最后的出口。

假设每次遇到岔道口都选择最右手边的岔路，直到碰到死胡同才回退到最近的岔道口选择另一条岔路。

（1）第一条路我们选择了ABDH，走到H发现是个死胡同，于是退回到D；下一个岔路选择I，发现I也是死胡同，于是再次退回到D；再下一个岔路选择J，发现J也是个死胡同，于是再次退回到D，此时D的所有岔路已经全部走完，而且均为死胡同，因此退回到D之前的岔道口B，重新选择岔路。

（2）接下来我们从B开始，选择了岔路E，在岔道口E中我们仍然进行枚举，依次选择了岔路K、L、M，发现均为死胡同，因此退回到E之前的岔道口B，B的两个岔路（D和E）都为死胡同，于是我们又回到了最开始的A，重新选择岔路。

（3）接下来我们从C开始，首先访问第一个岔路F，发现F是个死胡同，再退回到C，然后访问G，发现G是终点。至此。我们找到了从起点到终点的路径，DFS过程结束。

在这个例子中，整个DFS过程中先后访问节点的顺序为ABDHIJEKLMCFG。从这个例子中我们可以看出，DFS以深度为关键词，不遇到死胡同是不会退回到上一个岔道口的，所以我们说，深度优先搜索是一种枚举所有完整路径以遍历所有情况的搜索方法。

使用栈和递归可以更好地实现深度优先搜索，使用非递归也是可以实现DFS的，只不过一般情况下会比递归麻烦，在使用递归时，系统会调用一个叫系统栈的东西来存放递归中每一层的状态，因此使用递归来实现DFS的本质其实还是栈。

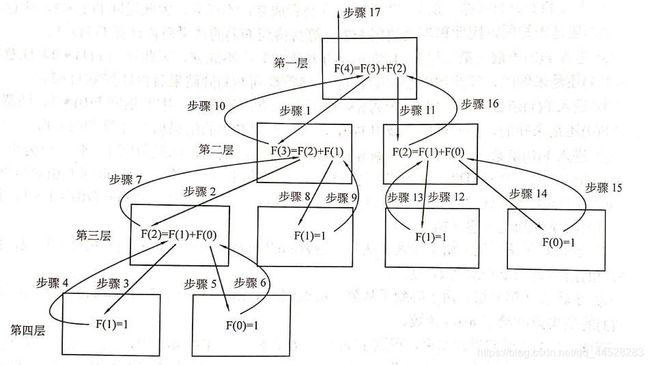
为了更好地说明递归的效果，下面我们用DFS的思想来分析斐波拉契数列的过程。

斐波拉契数列：F（0）=1，F（1）=1，F（n）=F（n-1）+F（n-2）

在递归图中我们可以看到，当n>1，F（n）就有两个分支，即把F（n）当作岔道口；而当n为1或0时，F（1）与F（0）就是迷宫的死胡同，在此处就需要返回结果。这样当遍历完所有路径后，就可以得到F（4）的值了。

抽象成代码，模板如下，这里我们用的是C/C++实现。

void DFS(Vertex V)
{
	visited[V] = true;
	for(V的每个邻接点W)
	{
		if(!visited[w]) DFS(W);
	}
}

下面通过一道例题让大家加深对DFS的理解

有n件物品，每件物品的重量为w[i]，价值为c[i]。现在需要选出若干件物品放入一个容量为V的背包中，使得在选入背包的物品重量和不超过容量V的前提下，让背包中物品的价值之和最大，求最大价值。（1<=n<=20）

#include
const int maxn = 30;
int n, v, maxValue = 0;//物品件数，背包容量，最大价值
int w[maxn], c[maxn];//w为每件物品重量，c为每件物品价值
//DFS，index为当前处理的物品编号
//sumW和sumC分别为当前总重量和当前总价值
void DFS(int index,int sumW,int sumC)
{
    if(index == n)
    {
        return ;//已经完成对n件物品的选择
    }
    DFS(index+1,sumW,sumC);//不选第index件物品
    //只有当加入第index件物品后未超过容量V，才能继续
    if(sumW+w[index] <= V)
    {
        if(sumC+c[index]>ans)
        {
            ans+=sumC+c[index];//更新最大价值maxValue
        }
        DFS(index+1,sumW+w[index],sumC+c[index]);//选第index件物品
    }
}

int main() 
{
	scanf("%d %d", &n, &v);
	for (int i = 0; i < n; i++) 
    {
		scanf("%d", &w[i]);//每件物品的重量
	}
	for (int i = 0; i < n; i++) 
    {
		scanf("%d", &c[i]);//每件物品的价值
	}
	DFS(0, 0, 0);//初始时为第0件物品、当前总重量和总价值均为0
	printf("%d\n",maxValue);
	return 0;
}

---

以下为其他关于DFS的练习题，点击题目即可进入对应网站进行练习，但是我比较懒所以还没有来的及做呜呜呜，我会在做完之后第一时间把题解补充在这篇博客下面，欢迎大家持续关注哦。

1.POJ 1312 棋盘问题

题目描述：在一个给定形状的棋盘（形状可能是不规则的）上面摆放棋子，棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列，请编程求解对于给定形状和大小的棋盘，摆放k个棋子的所有可行的摆放方案C。

输入：输入含有多组测试数据。
每组数据的第一行是两个正整数，n k，用一个空格隔开，表示了将在一个n*n的矩阵内描述棋盘，以及摆放棋子的数目。 n <= 8 , k <= n
当为-1 -1时表示输入结束。
随后的n行描述了棋盘的形状：每行有n个字符，其中 # 表示棋盘区域， . 表示空白区域（数据保证不出现多余的空白行或者空白列）。

输出：对于每一组数据，给出一行输出，输出摆放的方案数目C （数据保证C<2^31）。

测试样例：

输入
2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1
输出
2
1

AC代码（C/C++）：

#include
using namespace std;

int n,k;//n*n棋盘，总共放k个棋子
int sum;//记录总共可行的方案数目
//结构体---放下每个棋子之后的棋盘状态
struct p
{
    char qp[10][10];
    int before_row;
};
//此时的k为剩余棋子个数
void DFS(p p1,int k)
{
    //棋子用完，方案可行
    if(k==0)
    {
        sum++;
        return;
    }
    //棋子未用完，继续
    else
    {
        for(int i=p1.before_row+1;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(p1.qp[i][j]=='#')
                {
                    p p2;
                    p2 = p1;
                    p2.before_row = i;
                    //通过把这一列的格子设为‘.’的方式，用来实现在一列不会出现两个棋子
                    for(int m=i;m<n;m++)
                    {
                        p2.qp[m][j] = '.';
                    }
                    //进行迭代
                    DFS(p2,k-1);
                }
                else continue;
            }
        }
    }
}

int main()
{
    while(cin>>n>>k && n!=-1)
    {
        p p1;
        //初始化
        p1.before_row = -1;
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                cin>>p1.qp[i][j];
            }
        }
        sum = 0;
        DFS(p1,k);
        cout<<sum<<endl;
    }
    return 0;
}

2.POJ 3279 Fliptile
3.POJ 1426 Find The Multiple