【Machine Learning】23.Anomaly Detection 异常检测

异常数据的检测，这实际上也是一种无监督学习（因为不知道什么是异常）

1.导入

import numpy as np
import matplotlib.pyplot as plt
from utils import *

%matplotlib inline

文件utils.py的代码：

import numpy as np
import matplotlib.pyplot as plt

def load_data():
    X = np.load("data/X_part1.npy")
    X_val = np.load("data/X_val_part1.npy")
    y_val = np.load("data/y_val_part1.npy")
    return X, X_val, y_val

def load_data_multi():
    X = np.load("data/X_part2.npy")
    X_val = np.load("data/X_val_part2.npy")
    y_val = np.load("data/y_val_part2.npy")
    return X, X_val, y_val


def multivariate_gaussian(X, mu, var):
    """
    Computes the probability 
    density function of the examples X under the multivariate gaussian 
    distribution with parameters mu and var. If var is a matrix, it is
    treated as the covariance matrix. If var is a vector, it is treated
    as the var values of the variances in each dimension (a diagonal
    covariance matrix
    """
    
    k = len(mu)
    
    if var.ndim == 1:
        var = np.diag(var)
        
    X = X - mu
    p = (2* np.pi)**(-k/2) * np.linalg.det(var)**(-0.5) * \
        np.exp(-0.5 * np.sum(np.matmul(X, np.linalg.pinv(var)) * X, axis=1))
    
    return p
        
def visualize_fit(X, mu, var):
    """
    This visualization shows you the 
    probability density function of the Gaussian distribution. Each example
    has a location (x1, x2) that depends on its feature values.
    """
    
    X1, X2 = np.meshgrid(np.arange(0, 35.5, 0.5), np.arange(0, 35.5, 0.5))
    Z = multivariate_gaussian(np.stack([X1.ravel(), X2.ravel()], axis=1), mu, var)
    Z = Z.reshape(X1.shape)

    plt.plot(X[:, 0], X[:, 1], 'bx')

    if np.sum(np.isinf(Z)) == 0:
        plt.contour(X1, X2, Z, levels=10**(np.arange(-20., 1, 3)), linewidths=1)
        
    # Set the title
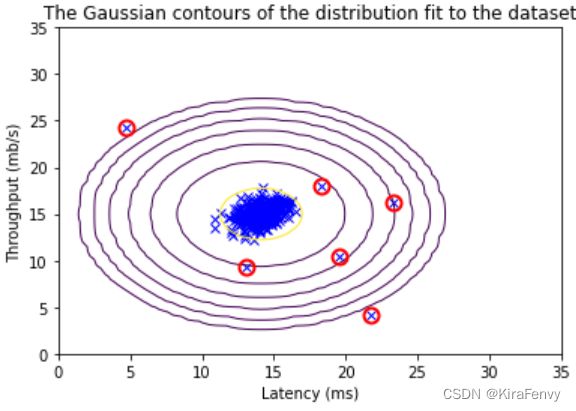
    plt.title("The Gaussian contours of the distribution fit to the dataset")
    # Set the y-axis label
    plt.ylabel('Throughput (mb/s)')
    # Set the x-axis label
    plt.xlabel('Latency (ms)')

2.Anomaly Detection 异常检测

2.1 问题描述

在本练习中，您将实现异常检测算法以检测服务器计算机中的异常行为。

数据集包含两个特征：

• 吞吐量（mb/s）和
• 每个服务器的响应延迟（ms）。

当您的服务器运行时，您收集了$m=307$它们的行为示例，因此有一个未标记的数据集$\{x^{(1)},\dots ,x^{(m)}\}$.

• 您怀疑这些示例中的绝大多数是服务器正常运行的“正常”（非异常）示例，但也可能有一些服务器在该数据集中异常运行的示例。

您将使用高斯模型来检测您的数据集。

• 您将首先从2D数据集开始，该数据集将允许您可视化算法正在做什么。
• 在该数据集上，您将拟合高斯分布，然后找到概率非常低的值，因此可以认为是异常。
• 之后，您将把异常检测算法应用于具有多个维度的更大数据集。

2.2 数据集

您将从加载此任务的数据集开始。

• 下面显示的load_data（）函数将数据加载到变量X_train、X_val和y_val中
• 您将使用X_train拟合高斯分布
• 您将使用X_val和y_val作为交叉验证集来选择阈值并确定异常与正常示例

# Load the dataset
X_train, X_val, y_val = load_data()

查看前五条数据

# Display the first five elements of X_train
print("The first 5 elements of X_train are:\n", X_train[:5])

# Display the first five elements of X_val
print("The first 5 elements of X_val are\n", X_val[:5]) 

# Display the first five elements of y_val
print("The first 5 elements of y_val are\n", y_val[:5])  

检查shape

print ('The shape of X_train is:', X_train.shape)
print ('The shape of X_val is:', X_val.shape)
print ('The shape of y_val is: ', y_val.shape)

The shape of X_train is: (307, 2)
The shape of X_val is: (307, 2)
The shape of y_val is:  (307,)

数据可视化：

对于这个数据集，您可以使用散点图来可视化数据（“X_train”），因为它只有两个属性可以绘制（吞吐量和延迟）

# Create a scatter plot of the data. To change the markers to blue "x",
# we used the 'marker' and 'c' parameters
plt.scatter(X_train[:, 0], X_train[:, 1], marker='x', c='b') 

# Set the title
plt.title("The first dataset")
# Set the y-axis label
plt.ylabel('Throughput (mb/s)')
# Set the x-axis label
plt.xlabel('Latency (ms)')
# Set axis range
plt.axis([0, 30, 0, 30])
plt.show()

2.3 高斯分布

To perform anomaly detection, you will first need to fit a model to the data’s distribution. 首先要把模型匹配数据分布才能执行异常检测

• Given a training set $\{x^{(1)},...,x^{(m)}\}$ you want to estimate the Gaussian distribution for each of the features $x_i$.

• Recall that the Gaussian distribution is given by

  $$p(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{\exp }^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

  where $\mu$ is the mean and ${\sigma }^2$ controls the variance.

• For each feature $i=1\dots n$, you need to find parameters ${\mu }_i$ and ${\sigma }_i^2$ that fit the data in the $i$-th dimension $\{x_i^{(1)},...,x_i^{(m)}\}$ (the $i$-th dimension of each example).

2.3.1 Estimating parameters for a Gaussian

Your task is to complete the code in estimate_gaussian below.

Exercise 1

Please complete the estimate_gaussian function below to calculate mu (mean for each feature in X)and var (variance for each feature in X).

You can estimate the parameters, (${\mu }_i$, ${\sigma }_i^2$), of the $i$-th
feature by using the following equations. To estimate the mean, you will
use: 平均值的计算公式

$${\mu }_i=\frac{1}{m}\sum _{j=1}^m{x}_i^{(j)}$$

and for the variance you will use: 方差的计算公式
$${\sigma }_i^2=\frac{1}{m}\sum _{j=1}^m(x_i^{(j)}-{\mu }_i{)}^2$$

# UNQ_C1
# GRADED FUNCTION: estimate_gaussian

def estimate_gaussian(X): 
    """
    Calculates mean and variance of all features 
    in the dataset
    
    Args:
        X (ndarray): (m, n) Data matrix
    
    Returns:
        mu (ndarray): (n,) Mean of all features
        var (ndarray): (n,) Variance of all features
    """

    m, n = X.shape
    
    ### START CODE HERE ### 
    mu = np.mean(X,axis = 0)#别忘了要指定轴
    var = np.mean((X - mu)**2,axis = 0) ##注意**2是在sum里面的
    ### END CODE HERE ### 
        
    return mu, var

函数调用：

# Estimate mean and variance of each feature
mu, var = estimate_gaussian(X_train)              

print("Mean of each feature:", mu)
print("Variance of each feature:", var)

Mean of each feature: [14.11222578 14.99771051]
Variance of each feature: [1.83263141 1.70974533]

# Returns the density of the multivariate normal
# at each data point (row) of X_train
p = multivariate_gaussian(X_train, mu, var)

#Plotting code 
visualize_fit(X_train, mu, var)

2.3.2 选择阈值

已经估计了高斯参数，您可以研究在给定这种分布的情况下，哪些示例具有非常高的概率，哪些示例的概率非常低。

• 低概率的例子更可能是我们数据集中的异常。
• 确定哪些示例是异常的一种方法是基于交叉验证集选择阈值。

在本节中，您将完成“select_threshold”中的代码，以使用交叉验证集上的$F_1$分数选择阈值$\epsilon$。

• For this, we will use a cross validation set
  $\{(x_{\mathrm{cv}}^{(1)},y_{\mathrm{cv}}^{(1)}),\dots ,(x_{\mathrm{cv}}^{(m_{\mathrm{cv}})},y_{\mathrm{cv}}^{(m_{\mathrm{cv}})})\}$, where the label $y=1$ corresponds to an anomalous example, and $y=0$ corresponds to a normal example. y=1代表异常数据，y=0代表正常数据
• For each cross validation example, we will compute $p(x_{\mathrm{cv}}^{(i)})$. The vector of all of these probabilities $p(x_{\mathrm{cv}}^{(1)}),\dots ,p(x_{\mathrm{cv}}^{(m_{\mathrm{cv})}})$ is passed to select_threshold in the vector p_val.
• The corresponding labels $y_{\mathrm{cv}}^{(1)},\dots ,y_{\mathrm{cv}}^{(m_{\mathrm{cv})}}$ is passed to the same function in the vector y_val.

Exercise 2

Please complete the select_threshold function below to find the best threshold to use for selecting outliers based on the results from a 验证集validation set (p_val) and the ground truth (y_val). 完成下列函数

• In the provided code select_threshold, 已经有一个循环将尝试$\epsilon$的许多不同值，并根据$F_1$得分选择最佳$\epsilon$。

• 通过选择epsilon作为阈值来计算F1分数，并将值放在“F1”中。

  • Recall that if an example $x$ has a low probability $p(x)<\epsilon$, then it is classified as an anomaly. 如果x的概率小于阈值，就是异常数据

  • Then, you can compute precision 准确率（预测当中正确预测概率） and recall 召回率（阳性当中被正确预测概率） by:
    $$\begin{array}{rlr}prec& =& \frac{tp}{tp+fp}\\ rec& =& \frac{tp}{tp+fn},\end{array}$$ where

    • $tp$ is the number of true positives: the ground truth label says it’s an anomaly and our algorithm correctly classified it as an anomaly. 真阳性
    • $fp$ is the number of false positives: the ground truth label says it’s not an anomaly, but our algorithm incorrectly classified it as an anomaly. 假阳性
    • $fn$ is the number of false negatives: the ground truth label says it’s an anomaly, but our algorithm incorrectly classified it as not being anomalous. 假阴性

  • The $F_1$ score is computed using precision ($prec$) and recall ($rec$) as follows: 计算F1分数的公式
    $$F_1=\frac{2\cdot prec\cdot rec}{prec+rec}$$

Implementation Note:
In order to compute $tp$, $fp$ and $fn$, you may be able to use a vectorized implementation rather than loop over all the examples. 使用向量化的实现方式而不是循环

代码填空：

下面代码选择epsilon的方法是把概率最大值和最小值区间内分成一千份，然后遍历

# UNQ_C2
# GRADED FUNCTION: select_threshold

def select_threshold(y_val, p_val): 
    """
    Finds the best threshold to use for selecting outliers 
    based on the results from a validation set (p_val) 
    and the ground truth (y_val)
    
    Args:
        y_val (ndarray): Ground truth on validation set
        p_val (ndarray): Results on validation set
        
    Returns:
        epsilon (float): Threshold chosen 
        F1 (float):      F1 score by choosing epsilon as threshold
    """ 

    best_epsilon = 0
    best_F1 = 0
    F1 = 0
    
    step_size = (max(p_val) - min(p_val)) / 1000
    
    for epsilon in np.arange(min(p_val), max(p_val), step_size):
    
        ### START CODE HERE ### 
        predictions = # Your code here to calculate predictions for each example using epsilon as threshold
        
        tp = # Your code here to calculate number of true positives
        fp = # Your code here to calculate number of false positives
        fn = # Your code here to calculate number of false negatives
        
        prec = # Your code here to calculate precision
        rec = # Your code here to calculate recall
        
        F1 = # Your code here to calculate F1
        ### END CODE HERE ### 
        
        if F1 > best_F1:
            best_F1 = F1
            best_epsilon = epsilon
        
    return best_epsilon, best_F1

答案：

    for epsilon in np.arange(min(p_val), max(p_val), step_size):
        ### START CODE HERE ### 
        predictions = (p_val < epsilon)
        
        tp = np.sum((predictions == 1) & (y_val == 1))
        fp = np.sum((predictions == 1) & (y_val == 0))# Your code here to calculate number of false positives
        fn = np.sum((predictions == 0) & (y_val == 1))# Your code here to calculate number of false negatives
        
        prec = tp / (tp + fp)  
        rec = tp / (tp + fn)
        
        F1 = 2 * prec * rec / (prec + rec)# Your code here to calculate F1
        ### END CODE HERE ### 
        
        if F1 > best_F1:
            best_F1 = F1
            best_epsilon = epsilon
        
    return best_epsilon, best_F1

测试代码：

p_val = multivariate_gaussian(X_val, mu, var)
epsilon, F1 = select_threshold(y_val, p_val)

print('Best epsilon found using cross-validation: %e' % epsilon)
print('Best F1 on Cross Validation Set: %f' % F1)

Best epsilon found using cross-validation: 8.990853e-05
Best F1 on Cross Validation Set: 0.875000

可视化异常数据

# Find the outliers in the training set 
outliers = p < epsilon

# Visualize the fit
visualize_fit(X_train, mu, var)

# Draw a red circle around those outliers
plt.plot(X_train[outliers, 0], X_train[outliers, 1], 'ro',
         markersize= 10,markerfacecolor='none', markeredgewidth=2)

2.4 在大数据集上的实践

In this dataset, each example is described by 11 features, capturing many more properties of your compute servers.

• The load_data() function shown below loads the data into variables X_train_high, X_val_high and y_val_high
  • _high is meant to distinguish these variables from the ones used in the previous part
  • We will use X_train_high to fit Gaussian distribution
  • We will use X_val_high and y_val_high as a cross validation set to select a threshold and determine anomalous vs normal examples
• 下面显示的“load_data（）”函数将数据加载到变量“X_train_high”、“X_val_high”和“y_val_high”中`
  • “_high”意在将这些变量与前一部分中使用的变量区分开来
  • 我们将使用“X_train_high”来拟合高斯分布
  • 我们将使用“X_val_high”和“y_val_high”作为交叉验证集来选择阈值并确定异常与正常示例

加载数据

# load the dataset
X_train_high, X_val_high, y_val_high = load_data_multi()

查看数据维度

print ('The shape of X_train_high is:', X_train_high.shape)
print ('The shape of X_val_high is:', X_val_high.shape)
print ('The shape of y_val_high is: ', y_val_high.shape)

进行异常检测

The code below will use your code to

• Estimate the Gaussian parameters (${\mu }_i$ and ${\sigma }_i^2$)
• Evaluate the probabilities for both the training data X_train_high from which you estimated the Gaussian parameters, as well as for the the cross-validation set X_val_high. 评估用于估计高斯参数的训练数据“X_train_high”以及交叉验证集“X_val_high”的概率。
• Finally, it will use select_threshold to find the best threshold $\epsilon$.

# Apply the same steps to the larger dataset

# Estimate the Gaussian parameters
mu_high, var_high = estimate_gaussian(X_train_high)

# Evaluate the probabilites for the training set
p_high = multivariate_gaussian(X_train_high, mu_high, var_high)

# Evaluate the probabilites for the cross validation set
p_val_high = multivariate_gaussian(X_val_high, mu_high, var_high)

# Find the best threshold
epsilon_high, F1_high = select_threshold(y_val_high, p_val_high)

print('Best epsilon found using cross-validation: %e'% epsilon_high)
print('Best F1 on Cross Validation Set:  %f'% F1_high)
print('# Anomalies found: %d'% sum(p_high < epsilon_high))


Best epsilon found using cross-validation: 1.377229e-18
Best F1 on Cross Validation Set:  0.615385
# Anomalies found: 117

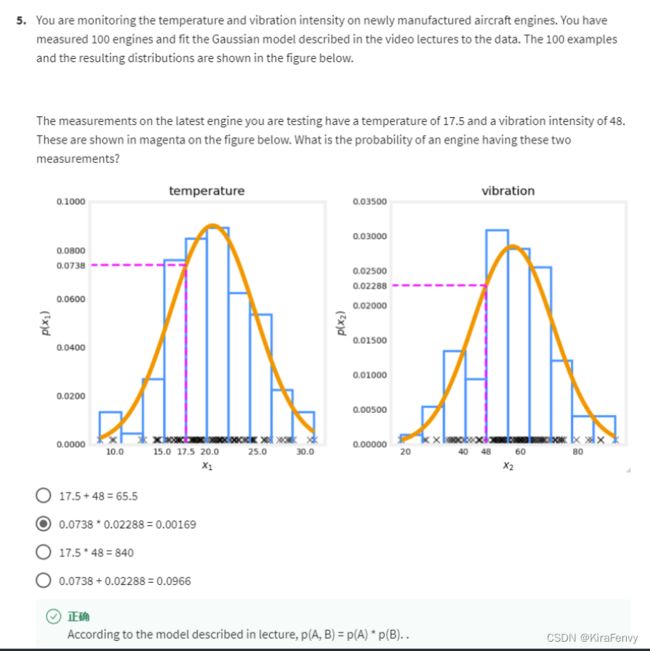
3.课后题

1. 监督学习和异常检测的使用：

• 您正在构建一个系统来检测数据中心中的计算机是否出现故障。您有10000个数据点计算机运行良好，并且没有来自计算机的数据发生故障。使用异常检测
• 您正在构建一个系统来检测数据中心中的计算机是否出现故障。你有10000个数据点计算机运行良好，10000个计算机数据点出现故障。使用监督学习

2. 上面的使用场景很容易判断，但要是有已知异常数据但极少要怎么办？

将异常发动机的数据（与一些正常发动机一起）进行交叉验证和/或测试

3. 阈值变小了，更少的数据会被分配为异常数据
   

4. 你正在监测新制造的飞机发动机的温度和振动强度。测量了100个引擎，并将视频讲座中描述的高斯模型与数据拟合。100个示例所得分布如下图所示。
   您正在测试的最新发动机的测量值温度为17.5，振动强度为48。下图中以洋红色表示。发动机有这两种情况的概率是多少