想要精通算法和SQL的成长之路 - 二叉树的序列化和反序列化问题
想要精通算法和SQL的成长之路 - 二叉树的序列化和反序列化问题
- 前言
- 一. 二叉树的层序遍历(BFS)
- 二. 二叉树的序列化与反序列化
-
- 2.1 序列化操作
- 2.2 反序列化操作
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 二叉树的层序遍历(BFS)
二叉树的层序遍历
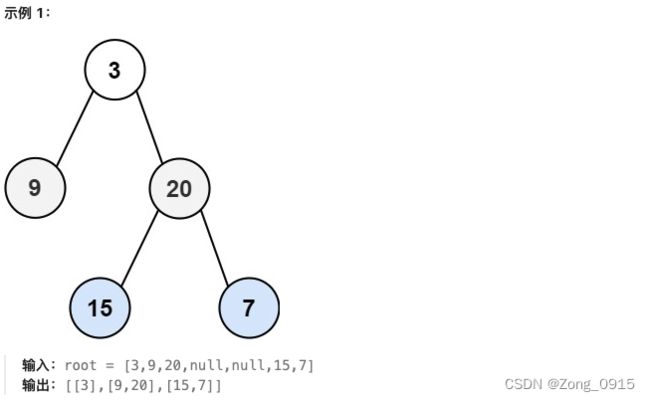
像这种从上至下并且按层打印的,可以称之为二叉树的广度优先搜索(BFS)。而这类算法往往借助队列的一个先入先出特性来实现。
那么有这么几个步骤:
1.特殊处理还有初始化动作。
List<List<Integer>> res = new ArrayList<>();
// 树为空,返回空数组
if (root == null) {
return res;
}
// 初始化队列
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
2.BFS循环:
while (!queue.isEmpty()) {
// 该层的打印结果
ArrayList<Integer> tmp = new ArrayList<>();
// 将当前层(队列内的元素)全部打印
for (int i = queue.size(); i > 0; i--) {
// 队首先出
TreeNode node = queue.poll();
tmp.add(node.val);
// 从左往右添加元素(先进先出)
if (node.left != null) {
tmp.add(node.left.val);
}
if (node.right != null) {
tmp.add(node.right.val);
}
}
// 当前层的遍历结果加入到最终结果集中
res.add(tmp);
}
最终完整代码如下:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
// 树为空,返回空数组
if (root == null) {
return res;
}
// 初始化队列
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
// 该层的打印结果
ArrayList<Integer> tmp = new ArrayList<>();
// 将当前层(队列内的元素)全部打印
for (int i = queue.size(); i > 0; i--) {
// 队首先出
TreeNode node = queue.poll();
tmp.add(node.val);
// 从左往右添加元素(先进先出)
if (node.left != null) {
tmp.add(node.left.val);
}
if (node.right != null) {
tmp.add(node.right.val);
}
}
// 当前层的遍历结果加入到最终结果集中
res.add(tmp);
}
return res;
}
二. 二叉树的序列化与反序列化
原题链接
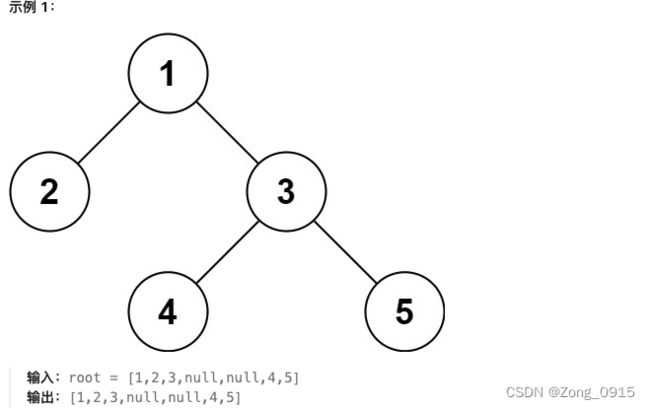
从题目来看,序列化的操作就是:从上往下,从左往右的一个层级遍历。那么在做这个题目之前,我们可以看下这个题目:
那么我们回归本题,本题和1.1小节的题目有啥不同?
- 如果是空节点,我们要输出
null。 - 我们还要根据序列化的结果,反序列化回一颗二叉树。
我们依旧可以使用队列来解决。
2.1 序列化操作
首先,特判以及队列的初始化操作:
if (root == null) {
return "[]";
}
StringBuilder res = new StringBuilder("[");
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
顺带提一嘴,希望大家养成良好的编码习惯,关于字符串的equal比较,常量放在前面,变量放后面,避免不必要的空指针。
BFS递归操作:
while (!queue.isEmpty()) {
// 队列先进先出,从队首开始出队
for (int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
// 只不过这里多加了一个判断而已,如果是空节点,我们添加null
if (node == null) {
res.append("null,");
continue;
}
// 否则,非空,添加当前节点的值
res.append(node.val + ",");
// 由于上面已经加了null的判断了,这里直接按顺序先加左节点,再加右节点即可。
queue.add(node.left);
queue.add(node.right);
}
}
最后就是收尾工作:我们对于结尾的值,要把多余的逗号去除。
// 删除最后一个多余的逗号
res.deleteCharAt(res.length() - 1);
res.append("]");
return res.toString();
最终完整代码如下:
public String serialize(TreeNode root) {
if (root == null) {
return "[]";
}
StringBuilder res = new StringBuilder("[");
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
// 队列先进先出,从队首开始出队
for (int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
// 只不过这里多加了一个判断而已,如果是空节点,我们添加null
if (node == null) {
res.append("null,");
continue;
}
// 否则,非空,添加当前节点的值
res.append(node.val + ",");
// 由于上面已经加了null的判断了,这里直接按顺序先加左节点,再加右节点即可。
queue.add(node.left);
queue.add(node.right);
}
}
// 删除最后一个多余的逗号
res.deleteCharAt(res.length() - 1);
res.append("]");
return res.toString();
}
2.2 反序列化操作
同样地,特判以及队列的初始化操作:
if ("[]".equals(data)) {
return null;
}
// 各个节点的值
String[] vals = data.substring(1, data.length() - 1).split(",");
// 第一个值必定是根节点(从上往下的特性)
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
LinkedList<TreeNode> queue = new LinkedList<TreeNode>() {{
add(root);
}};
BFS操作:
int index = 1;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
// 处理左节点
if (!"null".equals(vals[index])) {
node.left = new TreeNode(Integer.parseInt(vals[index]));
queue.add(node.left);
}
// 这里不管怎样都是要往后移动一位,如果是null,我们node.left就默认是null了。
index++;
if (!"null".equals(vals[index])) {
node.right = new TreeNode(Integer.parseInt(vals[index]));
queue.add(node.right);
}
index++;
}
完整代码:
public TreeNode deserialize(String data) {
if ("[]".equals(data)) {
return null;
}
String[] vals = data.substring(1, data.length() - 1).split(",");
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
LinkedList<TreeNode> queue = new LinkedList<TreeNode>() {{
add(root);
}};
int index = 1;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
// 处理左节点
if (!"null".equals(vals[index])) {
node.left = new TreeNode(Integer.parseInt(vals[index]));
queue.add(node.left);
}
// 这里不管怎样都是要往后移动一位,如果是null,我们node.left就默认是null了。
index++;
if (!"null".equals(vals[index])) {
node.right = new TreeNode(Integer.parseInt(vals[index]));
queue.add(node.right);
}
index++;
}
return root;
}