【数据结构】二叉树堆排序，TopK详解(第二章)

前言

✨笔者也仅是大一萌新，写博客为了记录和巩固知识✨

赠人玫瑰，手留余香，欢迎各位读者进行交流和建议

能与大家一起学习，一起进步是我的荣幸

如果这篇文章有帮助到您，还请留个赞支持一下哦

---

前情提要

二叉树第一章——初识二叉树

---

---

目录：

1. 二叉树的顺序结构
2. 堆的概念和结构
3. 实现堆的方法
   • ⭐建堆的时间复杂度
   • ⭐函数声明
   • ⭐交换函数
   • ⭐打印函数
   • ⭐初始化
   • ⭐清空函数
   • ⭐插入函数
   • ⭐向上调整法
   • ⭐删除函数
   • ⭐向下调整法
   • ⭐根结点，树的大小，判空三合一
4. 实现堆排序
   • ⭐方法一(不推荐)
   • ⭐方法二(直接成堆)
5. 实现TopK
   • ⭐什么是TopK
   • ⭐打印(实现)TopK
   • ⭐TopK输入数据
6. 总代码

---

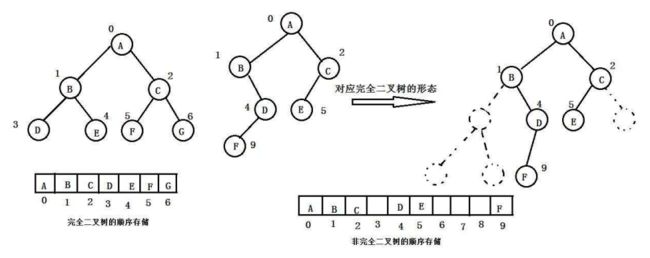
二叉树的顺序结构:

普通的二叉树不适合用数组来存储，因为可能会存在大量的空间浪费，所以适合使用顺序结构存储的通常为完全二叉树。而堆就是使用顺序结构来存储的(这里的堆和我们学内存的堆是不同的，一个是数据结构，一个是操作系统中管理内存的一块区域分段)。

---

堆的概念和结构:

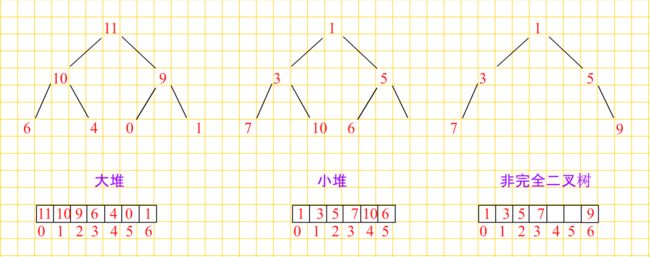
一个完全二叉树以顺序存储的方法存入一个一维数组中，那么这个堆可以分为:

大堆/大根堆:树中的父亲都大于等于孩子

小堆/小根堆:树中的父亲都小于等于孩子

堆主要用来解决:堆排序，TopK

堆的性质:

• 堆中某个结点的值总是不大于或不小于父亲的值
• 堆总是一棵完全二叉树

---

实现堆的方法

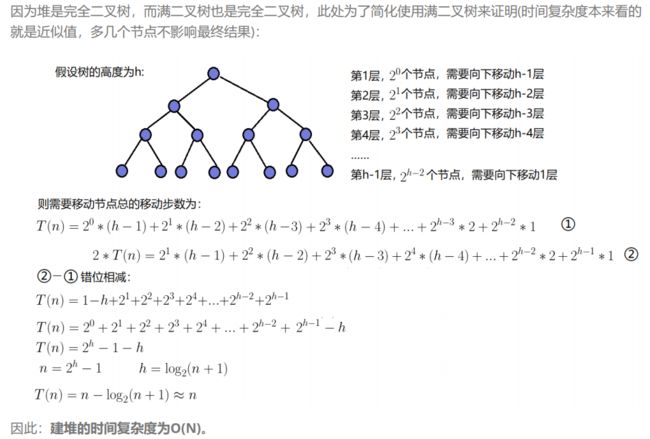
⭐ 建堆的时间复杂度：

---

⭐ 函数声明：

#pragma once

#include 
#include 
#include 
#include 
#include 

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	size_t size;
	size_t capacity;
}HP;
void Swap(HPDataType* pa, HPDataType* pb); //交换函数
void HeapPrint(HP* php); //打印函数
void HeapInit(HP* php); //初始化
void HeapDestroy(HP* php); //清空
void HeapPush(HP* php, HPDataType x); //插入
void HeapPop(HP* php); //删除
bool HeapEmpty(HP* php); //判空
size_t HeapSize(HP* php); //树的大小
HPDataType HeapTop(HP* php); //根结点
void AdjustUp(HPDataType* a, size_t child); //向上调整
void AdjustDown(HPDataType* a, size_t size, size_t root); //向下调整

---

⭐ 交换函数：

注意：形参接收实参的值，如果不用return的话出了该函数就会被销毁，必须要接收地址才能改变实参的值

void Swap(HPDataType* pa, HPDataType* pb) //交换
{
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

---

⭐ 打印函数：

直接进行遍历打印即可

void HeapPrint(HP* php)
{
	assert(php);
	for (size_t i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

---

⭐ 初始化：

防止杂乱数据出现我们都先置空

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;
}

---

⭐ 清空函数：

在释放空间后也要把指针置空防止出现野指针

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}

---

⭐ 插入函数：

要注意的是，我们不能像之前的线性表那样，只把数据放进去，在树中我们还需要进行调整，不然会破坏树的结构(比如:我在一个父节点为100的小堆中插入一个99，那么结构显然是不对的)，这时我们需要用到向上调整法

void HeapPush(HP* php, HPDataType x) //时间复杂度O(logN)
{
	assert(php);
	if (php->size == php->capacity) //朴实无华的扩容操作
	{
		size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			printf("realloc fail!");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x; //将x放入树中
	php->size++;
	AdjustUp(php->a, php->size - 1); //此时x在下标为size-1的位置
}

---

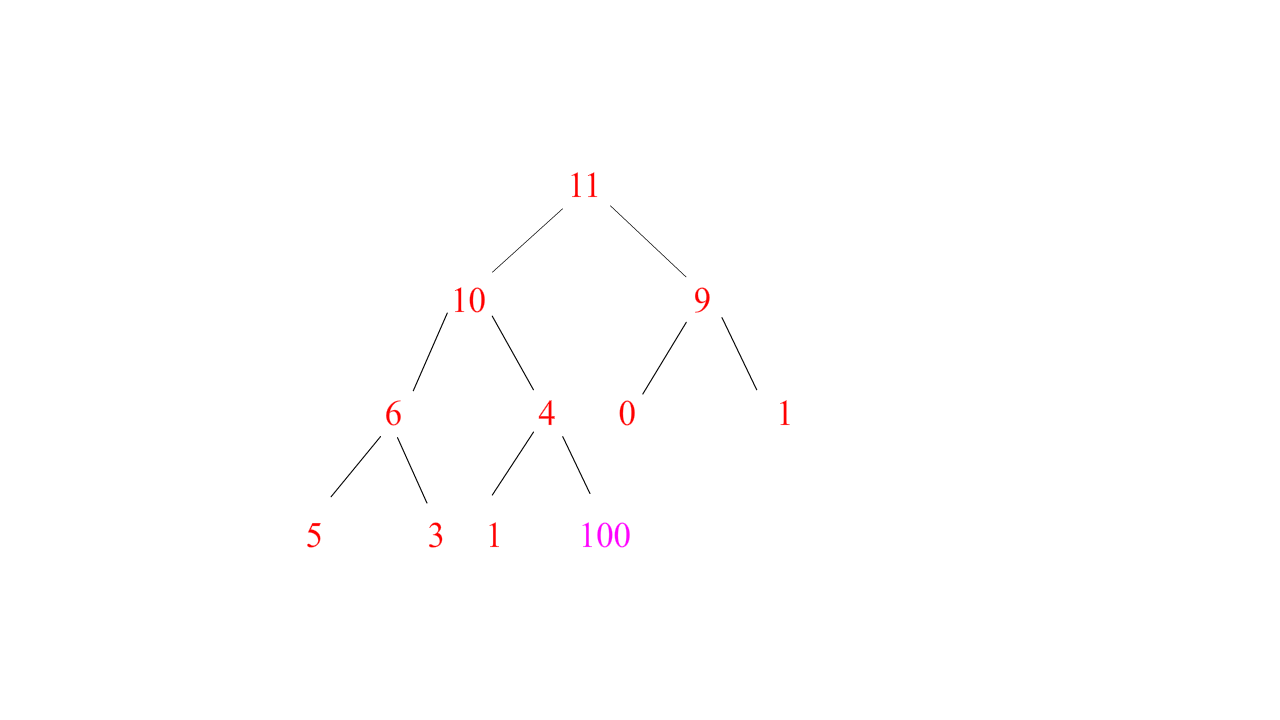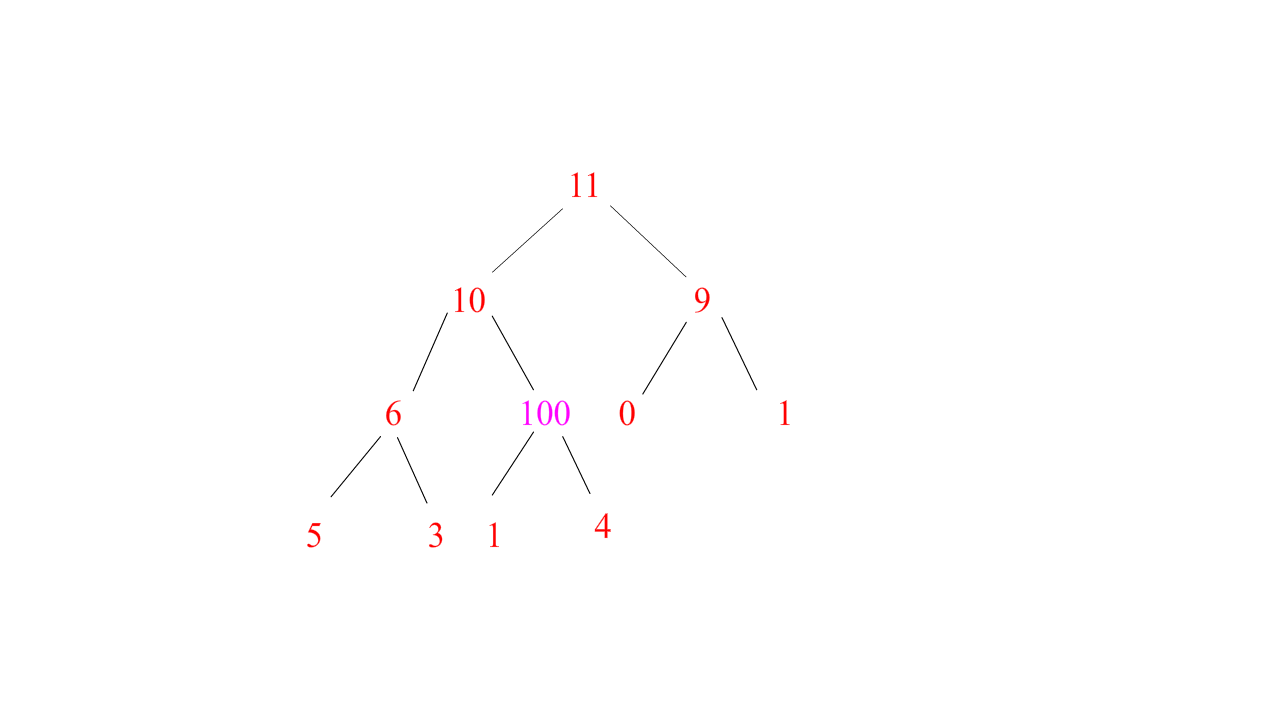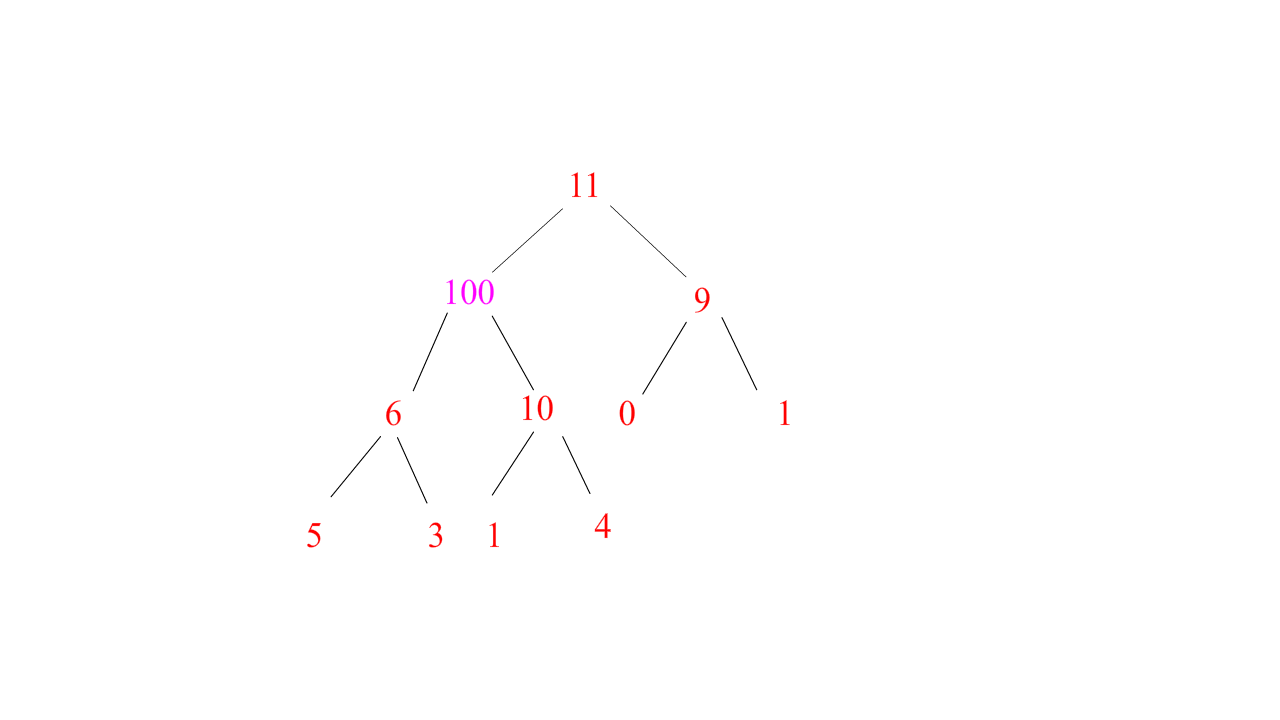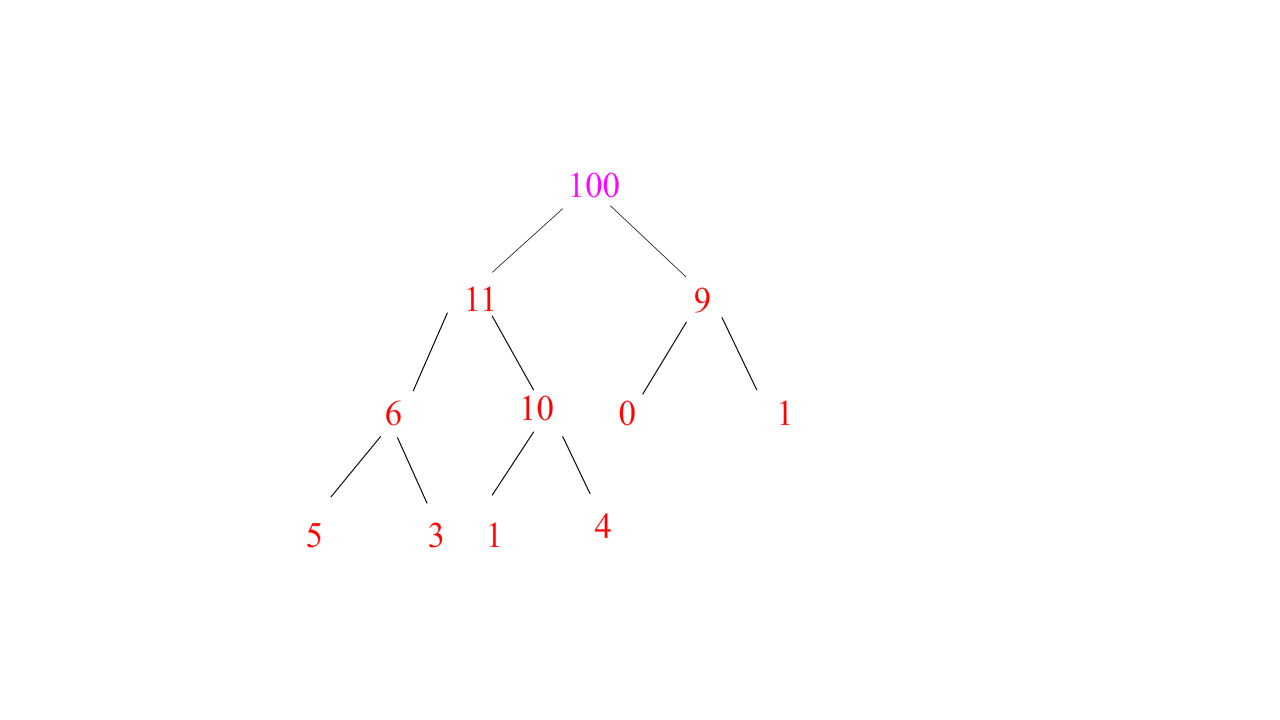
⭐ 向上调整法:

思路:

为了不让树的结构被破坏，我们需要调整一下不符合规则的插入数据，而插入的这个数据影响的是它这条路径的所有祖先，如下图的100影响的是11-10-4，所以我们只需要将100与这条路径的数据进行对比，满足规则就停下来，不满足规则就继续对比

图示(大堆演示)：

void AdjustUp(HPDataType* a, size_t child) //向上调整，形成大堆小堆
{
	//找下标
	size_t parent = (child - 1) / 2; //因为这里是整形，所以右孩子减一减二都一样
	while (child > 0)
	{
		if (a[child] < a[parent]) //大小堆切换
		{
			Swap(&a[child], &a[parent]); //传地址才能改变实参的值
			child = parent; //孩子结点下标更新，让孩子结点往上走继续判断是否形成大小堆
			parent = (child - 1) / 2; //父节点下标更新
		}
		else //当孩子结点已经大于/小于父节点形成大堆/小堆，循环停止
		{
			break;
		}
	}
}

---

⭐ 删除函数：

我们删除元素不是毫无章法的删，是删除最大/最小的数据(看是大堆还是小堆)，而最大/最小的数据就是堆顶的值，很多人会用顺序表的覆盖方法来删除堆顶，但是这样也是可能有破坏结构的风险！这时我们会用到向下调整法

void HeapPop(HP* php) //删除最大最小的数据(堆顶数据),时间复杂度O(logN)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]); //将最后一个元素和堆顶元素互换
	php->size--; //删除最后一个元素
	AdjustDown(php->a, php->size, 0);
}

---

⭐ 向下调整法:

思路:

与向上调整法类似，都是比较与交换的过程，但是向下调整法还需要判断左右孩子的大小

图示(大堆演示)：

void AdjustDown(HPDataType* a, size_t size, size_t root)
{
	size_t parent = root; //从根结点，也就是堆顶开始
	size_t child = parent * 2 + 1; //加一加二影响后面找谁大谁小，这里直接定为左孩子方便后面调整
	while (child < size)
	{
		//选出左右孩子谁更小
		if (child + 1 < size && a[child + 1] > a[child]) //通过下标比较左右孩子谁大谁小
		{
			++child;
		}
		//如果孩子小于父亲则交换
		if (a[child] > a[parent]) //与父节点比较，大于父节点就不是大堆，需要交换
		{
			Swap(&a[child], &a[parent]);
			parent = child; //更新下标
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

---

⭐ 根结点，树的大小，判空三合一：

都是很简单的函数，没啥讲的

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;
}
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

---

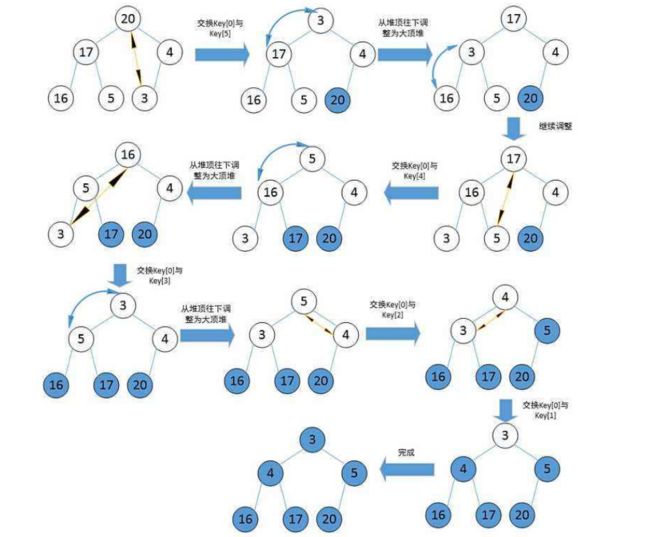
实现堆排序

⭐ 方法一(不推荐)：

理解到了插入和删除再理解排序应该不难，可以自己画个二叉树进行向上向下调整找找感觉

不过这种方法不推荐，这样排序还需要写一个堆才能够进行，其次它的空间复杂度为O(N)，还能够继续优化

图示(大堆演示)：

void HeapSort(int* a, int size)
{
	HP hp;
	HeapInit(&hp);
	//时间复杂度:O(N*logN)
	for (int i = 0; i < size; i++) //往堆中插入数据
	{
		HeapPush(&hp, a[i]);
	}
	size_t j = 0;
	//时间复杂度:O(N*logN)
	while (!HeapEmpty(&hp)) //判空，如果堆中不为NULL就继续
	{
		a[j] = HeapTop(&hp); //取走堆顶最大/最小元素
		j++;
		HeapPop(&hp); //删除当前堆顶元素，下一个就是次大/次小的元素，反复进行储存即可排序
	}
}

---

⭐ 方法二(直接成堆)：

假如我们升序建小堆，那么堆顶为最小的数，剩下的数关系全乱了，需要重新建堆，再选出次小的，这样反而更麻烦了！

所以我们排升序降序的方法应为:

升序：建大堆

降序：建小堆

向下调整流程图：

void HeapSort(int* a, int size) //堆排序 = 选择排序
{
	int n = 1;
    
    //向上调整法建,N*log(N)
	/*for (child = 1; child < size; child++)
	{
		AdjustUp(a, child);
	}*/
    
	//向下调整法建
	for (int n = (size - 1 - 1) / 2; n >= 0; --n) //O(n)，从倒数第一个非叶子结点开始找(最后一个结点的父亲)
	{
		AdjustDown(a, size, n);
	}
    
	size_t end = size - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

---

实现TopK

⭐ 什么是TopK：

TopK问题：在数据量比较大的情况，求出数据中前K个最大的元素或者最小的元素。

如英雄联盟艾欧尼亚区的玩家大约有700w人，需要计算排位分前5的玩家：

TopK最简单的方法就是排序，但是当数据量特别大的时候，数据就不能一下全部存入内存中，此时就需要用堆来解决问题:

1. 用数据集合中的前K个元素来建堆
   • 求前K个最大元素用小堆
   • 求前K个最小元素用大堆
2. 用剩余N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

---

⭐ 打印(实现)TopK：

时间复杂度：O(K+logK*(N-K))

空间复杂度：O(K);

void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kminHeap = (int*)malloc(sizeof(int) * k);
	assert(kminHeap);

	for (int i = 0; i < k; ++i)
	{
		kminHeap[i] = a[i]; //先将前K个放入kminheap
	}

	// 建小堆
	for (int j = (k - 1 - 1) / 2; j >= 0; --j) //从倒数第一个非叶子结点开始
	{
		AdjustDown(kminHeap, k, j); 
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (int i = k; i < n; ++i)
	{
		if (a[i] > kminHeap[0])
		{
			kminHeap[0] = a[i];
			AdjustDown(kminHeap, k, 0);
		}
	}

	for (int j = 0; j < k; ++j) //打印
	{
		printf("%d ", kminHeap[j]);
	}
	printf("\n");
	free(kminHeap);
    kiminHeap = NULL;
}

---

⭐ TopK输入数据：

void TestTopk()
{
	int n = 10000;
 	int* a = (int*)malloc(sizeof(int)*n);
 	srand(time(0));
 	for (size_t i = 0; i < n; ++i)
 	{
 		a[i] = rand() % 1000000;
 	}
 	a[665] = 1001112;
 	a[1231] = 1005652;
 	a[531] = 1000003;
 	a[51] = 1000014;
 	a[12] = 1000225;
 	a[35] = 1000006;
 	a[9999] = 1999999;
 	a[9822] = 1314520;
	a[1] = 1003030;
 	a[0] = 1100000;
 	PrintTopK(a, n, 10);
}

---

总代码：

因为太懒所以直接复制之前写的代码了= =，有什么错误还希望能够指出

#include "heap.h"
void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}
void HeapPrint(HP* php)
{
	assert(php);
	for (size_t i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}
void HeapDestory(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}
void Swap(HPDataType* pa, HPDataType* pb) //交换
{
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
void AdjustUp(HPDataType* a, size_t child) //向上调整，形成大堆小堆
{
	//找下标
	size_t parent = (child - 1) / 2; //右孩子减一减二都一样
	while (child > 0)
	{
		if (a[child] > a[parent]) //大小堆切换
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			printf("realloc fail!");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}
void AdjustDown(HPDataType* a, size_t size, size_t root)
{
	size_t parent = root;
	size_t child = parent * 2 + 1;
	while (child < size)
	{
		//选出左右孩子谁更小
		if (child + 1 < size && a[child + 1] < a[child])
		{
			++child;
		}
		//如果孩子小于父亲则交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(HP* php) //堆顶数据，最小/最大
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}
bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;
}
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

---

#pragma once

#include 
#include 
#include 
#include 
#include 

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	size_t size;
	size_t capacity;
}HP;
void Swap(HPDataType* pa, HPDataType* pb);
void HeapPrint(HP* php);
void HeapInit(HP* php);
void HeapDestory(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
bool HeapEmpty(HP* php);
size_t HeapSize(HP* php);
HPDataType HeapTop(HP* php);
void AdjustUp(HPDataType* a, size_t child);
void AdjustDown(HPDataType* a, size_t size, size_t root);

---

#include "heap.h"
void TestHeap()
{
	HP hp;
	HeapInit(&hp);
	HeapPush(&hp, 0);
	HeapPush(&hp, 1);
	HeapPush(&hp, 4);
	HeapPush(&hp, 2);
	HeapPush(&hp, 8);
	HeapPush(&hp, 9);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapDestory(&hp);
}
//要求:时间复杂度O(N*logN)
//     空间复杂度O(1)
//void HeapSort(int* a, int size)
//{
//	HP hp;
//	HeapInit(&hp);
//	//O(N*logN)
//	for (int i = 0; i < size; i++)
//	{
//		HeapPush(&hp, a[i]);
//	}
//	size_t j = 0;
//	//O(N*logN)
//	while (!HeapEmpty(&hp))
//	{
//		a[j] = HeapTop(&hp);
//		j++;
//		HeapPop(&hp);
//	}
//}
void HeapSort(int* a, int size) //堆排序 = 选择排序
{
	//向上建堆
	int n = 1;
	/*for (child = 1; child < size; child++)
	{
		AdjustUp(a, child);
	}*/
	//向下建堆
	for (int n = (size - 1 - 1) / 2; n >= 0; --n)
	{
		AdjustDown(a, size, n);
	}
	size_t end = size - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}
void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kminHeap = (int*)malloc(sizeof(int)*k);
	assert(kminHeap);

	for (int i = 0; i < k; ++i)
	{
		kminHeap[i] = a[i];
	}

	// 建小堆
	for (int j = (k - 1 - 1) / 2; j >= 0; --j)
	{
		AdjustDown(kminHeap, k, j);
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (int i = k; i < n; ++i)
	{
		if (a[i] > kminHeap[0])
		{
			kminHeap[0] = a[i];
			AdjustDown(kminHeap, k, 0);
		}
	}

	for (int j = 0; j < k; ++j)
	{
		printf("%d ", kminHeap[j]);
	}
	printf("\n");
	free(kminHeap);
}

void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int)*n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 1000000 + 5;
	a[2305] = 1000000 + 6;
	a[99] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[0] = 1000000 + 1000;
	PrintTopK(a, n, 10);
}
int main()
{
	/*TestHeap();*/
	int a[] = { 12,10,11,6,4,0,1,5,3,1,3 };
	HeapSort(a, sizeof(a) / sizeof(a[0]));
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	TestTopk();
	return 0;
}