排序算法——选择排序系列及性能测试

初识选择排序

选择排序是一种和冒泡排序一样简单的排序算法。它的思想非常简单，假设数组大小为n，每次从数组的待排序部分中选出一个最小的元素，放到数组最左侧，n轮筛选后，数组就整体有序了。

图解如下

假设准备对如下数组进行选择排序

先对数组的待排序部分进行遍历，选出最小的元素为1，将1放到数组最左侧

第二轮，对剩下的部分进行遍历，选出最小的元素为2，将2放到最左侧（和4交换）

如此以来，第三轮选出的元素是3，第四轮选出的是4…经过9轮选择后，数组整体有序

它的代码实现也非常简单

	public void selectSort(int[] array) {
		for (int i = 0; i < array.length; i++) {
			int minPos = i;
			for (int j = i + 1; j < array.length; j++) {
				if (array[minPos] > array[j]) {
					minPos = j;
				}
			}
			swap(array, i, minPos);
		}
	}

优化思路

思路一

双向选择

选择排序的优化思路比较有限，根据双向冒泡的优化经验，我们可以一轮遍历选出一个最大值和一个最小值，从而提高筛选的效率。

写成代码如下

	public void selectSortDual(int[] array) {
		int leftBorder = 0;
		int rightBorder = array.length - 1;
		while (leftBorder < rightBorder) {
			int minPos = leftBorder;
			int maxPos = leftBorder;
			for (int j = leftBorder + 1; j <= rightBorder; j++) {
				if (array[minPos] > array[j]) {
					minPos = j;
				}
				if (array[maxPos] < array[j]) {
					maxPos = j;
				}
			}
			swap(array, leftBorder, minPos);
            /* 下面的交换要注意，若恰好maxPos等于leftBorder，由于上面已经将leftBorder下标的元素交换到minPos了 */
			if (maxPos == leftBorder) {
				/* 若恰好maxPos为leftBorder，则下面对maxPos的交换要与minPos进行 */
				swap(array, rightBorder, minPos);
			} else {
				swap(array, rightBorder, maxPos);
			}
			leftBorder++;
			rightBorder--;
		}
	}

思路二（堆排序）

堆排序

其实，堆排序也是选择排序的一个变种。堆排序需要先对数组进行建堆（大顶堆或小顶堆），然后每次将堆顶元素和堆尾元素进行交换，随后将堆尾元素在逻辑上从堆中剔除，对剩余部分的堆进行调整，再将堆顶元素和当前堆尾元素交换，以此类推。每一轮排序都会将堆顶元素追加到数组末端的有序序列中，而堆顶元素就是每一轮选出来的最大或最小值，所以堆排序也属于选择排序。

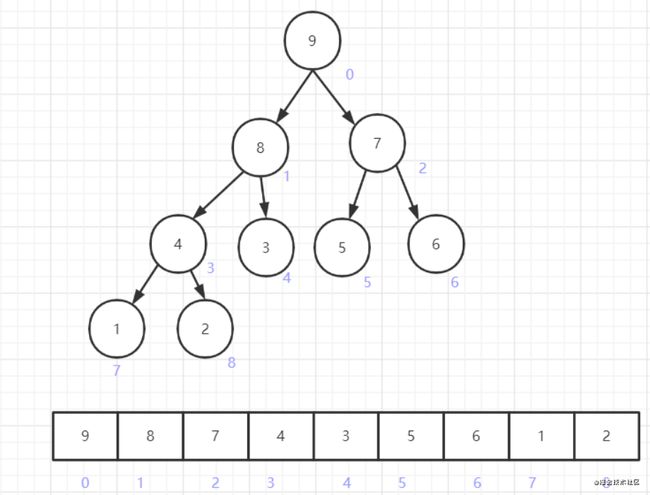
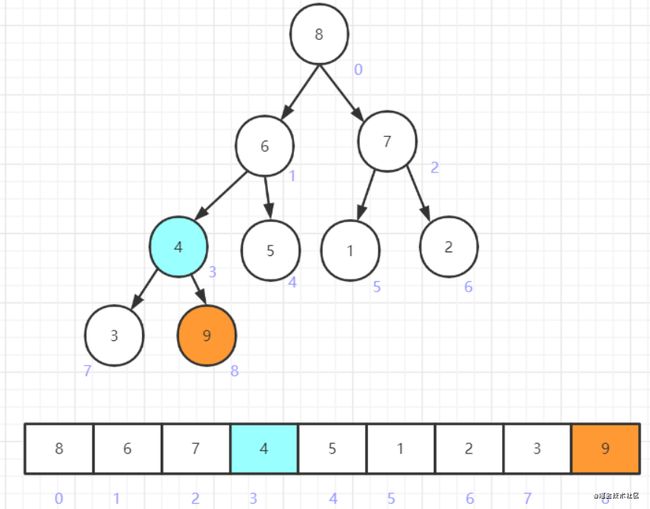
首先对堆进行一个简单的介绍。堆的本质就是一棵完全二叉树。而大顶堆，指的是堆顶元素（二叉树的根节点）要大于其左右子树的任意节点，而其余的每个非叶子节点的值，也要大于其左右子树的任意节点。下图即是一个大顶堆的逻辑结构图

可以看到堆顶元素9要大于其左右子节点8和7，节点8要大于其左右子节点4和3，7要大于其左右子节点5和6，4要大于其左右子节点1和2。这就使得堆顶元素是最大的元素。而二叉堆在实际使用中，常常以数组的形式进行存储，如下所示

紫色的数字表示元素在数组中的下标。堆从第一层开始，每一层从左往右编号，即是其在数组中存储的位置。容易得到如下的关系：

若堆中的一个节点在数组中的下标为n，若其有左右子节点，则

左子节点的下标为：2n + 1

右子节点的下标为：2n + 2

若其有父节点，则父节点的下标为：(n - 1) / 2

既然堆可以用数组的形式进行存储和表示，那么就可以对数组进行建堆，然后执行堆排序。堆排序的关键在于对初始数组进行建堆，以及交换了堆顶元素和堆尾元素后的调整

图解如下

假设准备对如下数组进行堆排序

先进行建堆操作（建大顶堆），根据数组，先将数组看成一个二叉树

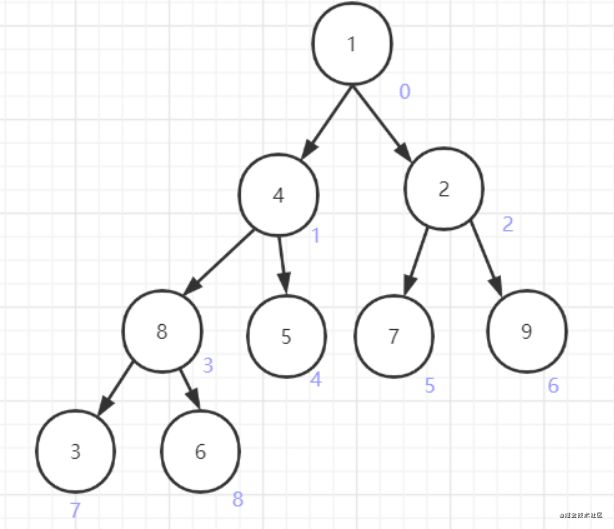
建堆的过程如下：从下往上，先找到第一个非叶子节点（没有任何子节点的节点，上图就是8），从这个节点开始，对所有非叶子节点依次进行下沉处理（向下调整）。下沉指的是，将节点与其子节点进行比较，若节点的值小于子节点中的较大者，则交换之。处理节点8，先把节点8及其子节点看成一个堆（局部堆），调整，以使这个局部堆满足大顶堆的特性。发现节点8不需要处理。

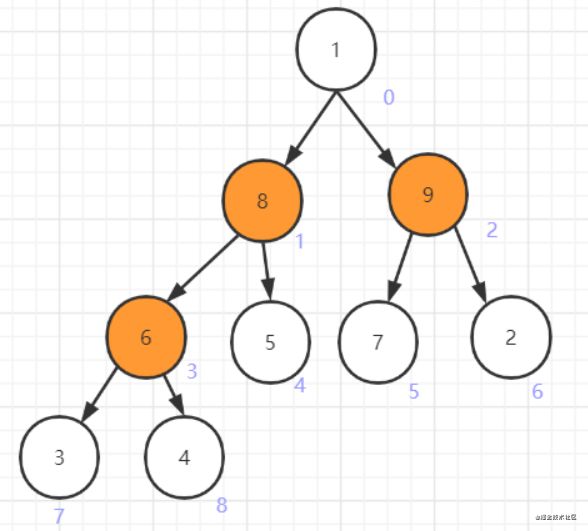
接着往前处理，到节点2，发现它比它的子节点要小，而子节点中的较大者是9，则交换2和9

接着处理节点4，发现它小于8，则交换它和8

注意下沉处理要下沉到尽可能底部的位置，4和8交换完后，继续处理4，发现4比它的子节点6要小，则交换4和6

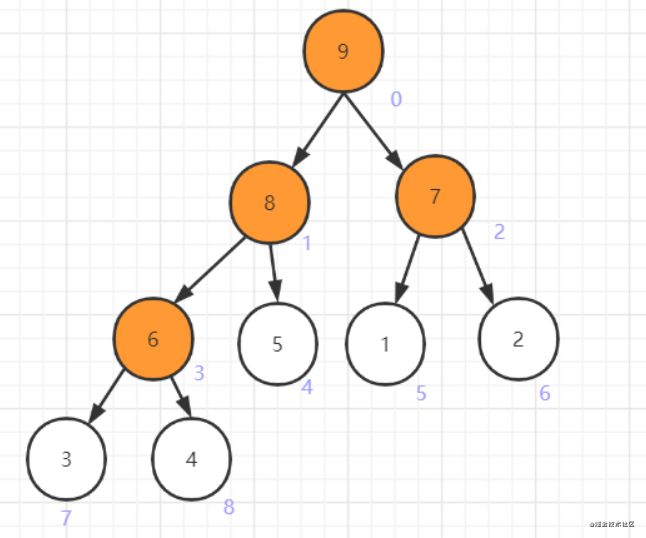
接着处理1，发现1小于9，则交换之

继续处理1，发现1小于7，交换之

如此以来，建堆操作完成，观察可知，现在的堆已经符合大顶堆的特性

建堆完毕后，执行如下操作：将堆顶元素和堆尾元素交换，然后将堆尾元素在逻辑上从堆中删除，将剩余元素看成一个堆，对堆顶元素进行向下调整，使其成为一个大顶堆。然后又将堆顶元素和当前堆的堆尾元素交换，把堆尾元素从堆中删除，对剩余元素继续调整…如此，即完成排序。

图解如下

首先，建堆完毕后的数组状态如下

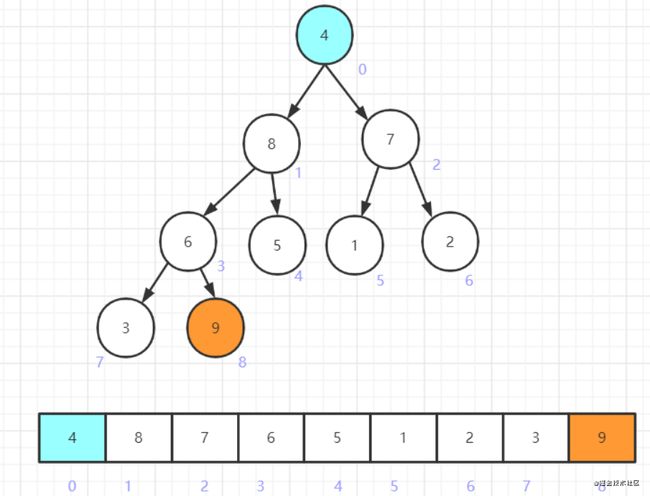
将堆顶元素和堆尾元素交换，即9和4交换

交换完毕后，将堆尾元素9在逻辑上从堆中删除。而剩余元素组成的堆，由于堆顶发生了变化，显然不满足大顶堆的性质，于是对新的堆顶进行向下调整

节点4比其子节点中的较大者8，要小，于是交换之

!

继续调整节点4，发现其比子节点6要小，则交换之

继续调整节点4，发现其只有一个左子节点3，且4大于3，则调整完毕（节点9已经在逻辑上从堆中移除，即堆中不再包含节点9）

剩余的元素组成的堆已符合大顶堆的性质

接着，继续将堆顶元素和当前堆的堆尾元素交换，即交换8和3

然后将节点8从堆中剔除掉，对当前堆顶元素3进行向下调整，发现只需要交换3和7，调整完毕后结果为

接着交换堆顶和堆尾，即交换7和2

调整堆

交换堆顶和堆尾

调整堆

…以此类推，最终数组有序

由此可见，堆排序的关键在于建堆，以及对节点的向下调整

写成代码如下

	public void heapSort(int[] array) {
		/* 先进行建堆 */
		buildHeap(array);
		/* 后执行循环 */
		for (int i = array.length - 1; i >= 0 ; i--) {
			/* 将堆顶元素和当前堆尾元素交换 */
			swap(array, 0, i);
			/* 调整堆 */
			adjustDown(array, 0, i - 1);
		}
	}

	/**
	 * 对数组进行建堆
	 * **/
	private void buildHeap(int[] array) {
		/* 从数组最右侧往左，即从堆的最下面往上，找到第一个非叶子节点, 对其进行向下调整 */
		/* 第一个非叶子节点，也就是最后一个节点的父节点 */
		/* 第一个非叶子节点之前的所有节点，都是非叶子节点了，都需要依次进行向下调整 */
		int firstNonLeafNode = (array.length - 1) / 2;
		for (int i = firstNonLeafNode; i >= 0 ; i--) {
			/* 对每个非叶子节点，进行向下调整 */
			adjustDown(array, i, array.length - 1);
		}
	}

	/**
	 * 对某个节点，进行向下调整
	 * @param targetPos 待调整的节点(数组下标)
	 * @param end    堆的终止位置(数组下标)
	 * @param array 堆的数组表示
	 * **/
	private void adjustDown(int[] array, int targetPos, int end) {
		int leftSonPos;
		/* 当左儿子没有超出堆的范围时，执行循环 */
		while ((leftSonPos = 2 * targetPos + 1) <= end) {
			/* 若右儿子存在，则选出左右儿子中较大者，否则则选左儿子 */
			int maxSonPos = leftSonPos + 1 <= end ?
					array[leftSonPos] > array[leftSonPos + 1] ? leftSonPos : leftSonPos + 1
					: leftSonPos;
			if (array[maxSonPos] > array[targetPos]) {
				swap(array, maxSonPos, targetPos);
				targetPos = maxSonPos;
			} else {
				/* 子儿子没有比target大的, 则调整结束 */
				break;
			}
		}
	}

注意，向下调整的过程，就是将需要调整的节点，下沉到合适的位置，考虑到先前插入排序时的优化，这里也可以采用单向赋值的方式，以避免频繁交换造成的性能开销。

性能测试

对选择排序系列的算法进行性能测试，结果如下

可见堆排序的性能完爆简单选择排序

扩展：堆排序的应用

Top K问题

从海量数据中筛选出前K个最大的数据

因为数据量特别大，对全部数据进行排序再取前K个数显然是不现实的，并且第K个以后的数是没有必要进行排序的，对K以后的数据进行排序显然浪费了性能。我们观察一下堆排序的性质，发现一个特点，无论大顶堆小顶堆，堆顶的元素总是最大的，或者最小的。如果一个大顶堆有K个元素，则堆顶的元素是这K个中最大的；如果一个小顶堆有K个元素，则堆顶的元素是这K个中最小的。那么假设一共有100个数据，要求找出前K个最大的数，可以这样想，我先取前K个元素，我只要知道当前这K个元素中最小的值，之后每次取一个新的元素，拿新元素和这个最小值比，若新元素小于这个最小值，说明新元素小于这所有的K个元素，则新元素不可能是前K个最大的数，直接抛弃之。若新元素比这个最小值大，那么把最小值剔除，换上这个新元素，再选出当前K个元素的最小值等待后续的比较。根据这个思路，只需要构建一个大小为K的小顶堆。先从海量数据中取前K个数，构建一个小顶堆。然后对K之后数，进行遍历，每次取一个数，和小顶堆的堆顶比较，若小于堆顶，则直接丢弃；若大于堆顶，则将该数和堆顶交换，并向下调整堆，维持其小顶堆的特征。因为只需要和堆顶这一个元素比较，并且小于堆顶的情况直接丢弃，只有大于堆顶的情况才需要调整堆，所以使得能够以较高的效率找到前K个最大的数，代码实现如下

	/**
	 * @param array 待查找的数组
	 * @param k 找到前K个最小的数
	 * **/
	public int[] findTheSmallestElements(int[] array, int k) {
		return findTheMostElements(array, k, false);
	}


	/**
	 * @param array 待查找的数组
	 * @param k 找到前K个最大的数
	 * **/
	public int[] findTheBiggestElements(int[] array, int k) {
		return findTheMostElements(array, k, true);
	}

	/**
	 * 找出前K个最大的，或者前K个最小的数
	 * @param biggest 是否是找最大的
	 * **/
	private int[] findTheMostElements(int[] array, int k, boolean biggest) {

		/* 找前K个最大的，则要建小顶堆; 找前K个最小的, 则要建大顶堆
		 * false 表示小顶堆
		 * true 表示大顶堆
		  * */
		boolean heapType = !biggest;

		/* 对前k个元素，建堆 */
		buildHeap(array,k - 1, heapType);
		/* 从第 k + 1 个元素 (下标为k) 开始遍历 */
		for (int i = k; i < array.length; i++) {
            /* 当前元素是否需要插入到前k个元素组成的堆中 */
			boolean needInsert = biggest ? array[i] > array[0] : array[i] < array[0];
			if (needInsert) {
				/* 若需要插入，则插入堆 */
				swap(array, 0, i);
				/* 调整堆，使其仍然是小顶堆/大顶堆 */
				adjustDown(array, 0, k - 1, heapType);
			}
			/* 否则,直接抛弃 */
		}
		int[] topKElements = new int[k];
        /* 取array数组的前k个元素,作为结果 */
		System.arraycopy(array, 0, topKElements, 0, k);
		return topKElements;
	}

	/**
	 * @param endPos 建堆的终止位置
	 * @param biggestTop 是否建大顶堆
	 * **/
	private void buildHeap(int[] array,int endPos, boolean biggestTop) {
		int firstNonLeafPos = (endPos - 1) / 2;
		for (int i = firstNonLeafPos; i >= 0 ; i--) {
			adjustDown(array, i, endPos, biggestTop);
		}
	}

	/**
	 * @param biggestTop 是否建大顶堆
	 * **/
	private void adjustDown(int[] array, int targetPos, int endPos, boolean biggestTop) {
		int leftSonPos;
		while ((leftSonPos = 2 * targetPos + 1) <= endPos) {
			int maxSonPos = leftSonPos, minSonPos = leftSonPos;
			if (leftSonPos + 1 <= endPos) {
				maxSonPos = array[leftSonPos] > array[leftSonPos + 1] ?
						(minSonPos = leftSonPos + 1) - 1 :
						leftSonPos + 1;
			}
			boolean needSwap = biggestTop ?
					array[maxSonPos] > array[targetPos] :
					array[minSonPos] < array[targetPos];
			int swapPos = biggestTop ? maxSonPos : minSonPos;
			if (needSwap) {
				swap(array, targetPos, swapPos);
				targetPos = swapPos;
			} else {
				break;
			}
		}
	}

优先级队列

队列在生活中随处可见。坐地铁时排队等车，在食堂排队打饭，去银行办理业务时也要取号排队。队列的本质就是一堆人，需要执行某个动作。最简单普通的队列就是按照先来后到的顺序依次排队，依次接收服务。但在某些场景下需要对排队的人进行一些优先级的设置，比如银行办理业务时，VIP客户的排队优先级就要高于普通客户，再比如，去食堂打饭时，如果有一个人已经10天没吃饭了，马上就要饿死了，是不是应该让他优先打饭，保证他能活过来。这些场景下，普通的队列就太死板了，无法满足需求，于是就有了优先级队列。优先级队列中的元素，不是严格按照先来后到的顺序排队的，而是优先级的高的元素，总是会排到优先级低的元素的前面，优先级相同的元素，再按先来后到的顺序排队。那么堆，这一数据结构，就能够满足这样的需求，因为它总是会把最大的，或者最小的元素，放在堆顶（数组的最前面）。

一个队列有2个基本操作：入队和出队

入队：一个人加入到队列中，进行排队

出队：轮到某个人办事了，将其移出队列

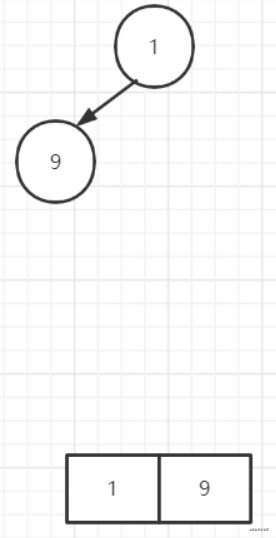
用堆的结构来表示，如下。先来一个优先级为1的人，进行排队

随后，来了一个优先级为9的人

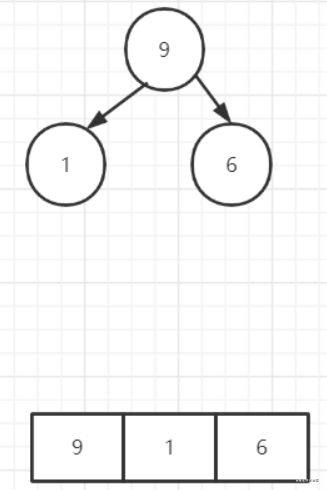
显然不满足大顶堆的性质，则对新来的9，进行调整，此时应该是向上调整，交换1和9即可

此时又来了一个6，发现仍然满足大顶堆的特性，则不做调整

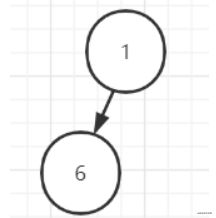
若此时，进行出队，则直接取出堆顶元素，节点9接受服务，数组变成了

对应的堆的逻辑结构就变成了

发现不满足大顶堆的特性，则进行调整，交换1和6即可

每次出队，都取数组的首元素，即堆顶元素，即能保证每次出队都是当前优先级最高的元素

其核心部分的逻辑为：

• 入队时，新加入的元素追加到数组末尾，也即堆尾，并需要对其进行向上调整，以满足大顶堆的性质。

• 出队时，移除数组的首元素，将剩余部分元素看成一个新的堆，并重新建堆

在此就不给出具体的代码实现了，有兴趣的读者可以自行尝试