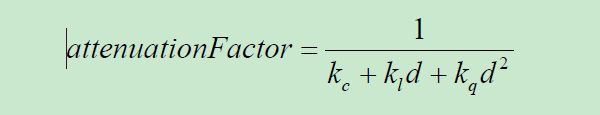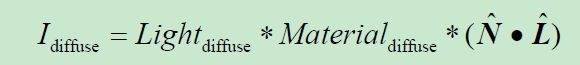openGL基础光照“ADS”（ Phone光照模型）（一）

openGL系列文章目录

前言

光照以不同的方式影响着我们世界的外观，有时甚至是很戏剧化的方式。当手电筒照射
在物体上时，我们会期望它面向光线的一侧看起来更亮。我们所居住的地球，在中午朝向
太阳时候被照得很亮，但随着它的自转，同一个地点的亮度会逐渐由白天转变为傍晚，直
到午夜变得完全黑暗。物体对光的反射也各不相同。物体除了颜色的差别，也可以具有不
同的反射特性。考虑两个物体，在都是绿色的情况下，其中一个是布制的，而另一个是抛
光钢材质的——那么后者看起来会更“闪亮”。

一、光照模型

我们所观察到的光是高能量源发出的光子，经过反射直到一些光子到达我们的眼睛的产
物。不幸的是，在计算上模拟这个自然过程是不可行的，因为这需要模拟并跟踪大量光子
的运动，即向我们的场景添加海量的对象（和矩阵）。因此，我们需要的是光照模型。
光照模型（Lighting model）有时也被称为着色模型（Shading model），在着色器编程存
在的情况下，这可能有点令人困惑。有时又使用术语反射模型（Reflection model），进一步
使术语复杂化。我们将尽力坚持使用简单而实用的术语。
现在最常见的光照模型称为“ADS”模型，因为它们基于标记为A、D 和S 的3 种类型
的反射。
环境光反射（Ambient reflection）模拟低级光照，影响场景中的所有物体。
漫反射（Diffuse reflection）根据光线的入射角度调整物体亮度。
镜面反射（Specular reflection）用以展示物体的光泽，通过在物体表面上，光线最
直接地反射到我们的眼睛的位置，策略性地放置适当大小的高光来实现。
ADS 模型可用于模拟不同的光照效果和各种材质。

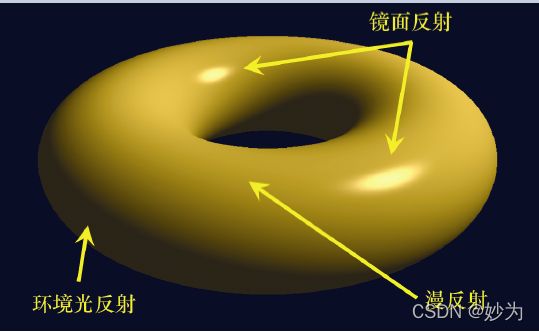
图一
ADS 模型可用于模拟不同的光照效果和各种材质。图一展示了位置光对于闪亮黄金环面的环境光反射、漫反射和镜面反射分量。回想一下，场景的绘制最终是由片段着色器为屏幕上的每个像素输出颜色而实现的。使用ADS 光照模型需要指定由于像素的RGBA输出值上的光照而产生的分量。因素包括：
光源类型及其环境、漫反射和镜面反射特性；
对象材质的环境、漫反射和镜面反射特征；
对象的材质指定为“光泽”；
光线照射物体的角度；
从中查看场景的角度。

二、光源

光源有许多类型，每种光源具有不同的特性，需要不同的步骤来模拟其效果。常见光源
类型有：
全局光（通常称为“全局环境光”，因为它仅包含环境光组件）；
定向光（或“远距离光”）；
位置光（或“点光源”）；
聚光灯。
全局环境光是最简单的光源模型。它没有光源位置——无论场景中的对象在何处，其上
的每个像素都有着相同的光照。全球环境光照模拟了现实世界中的一种光线现象，即光线
经过很多次反射，其光源和方向都已经无法确定。全局环境光仅具有环境光反射分量，用
RGBA 值设定；它没有漫反射或镜面反射分量。例如，全局环境光可以定义如下：
float globalAmbient[4] = { 0.6f, 0.6f, 0.6f, 1.0f };
RGBA 的取值范围为0～1，全局环境光通常被建模为偏暗的白光，其中RGB 各值设为
0～1 的相同的小数，alpha 设置为1。
定向光或远距离光也没有源位置，但它具有方向。它可以用来模拟光源距离非常远，以
至于光线接近平行的情况，例如阳光。通常在这种情况下，我们可能只对建模光照感兴趣，
而对发光的物体不感兴趣。定向光对物体的影响取决于光照角度，物体在朝向定向光的一
侧比在切向或相对侧更亮。建模定向光需要指定其方向（以向量形式）及其环境、漫反射
和镜面特征（以RGBA 值）。指向Z 轴负方向的红色定向光可以指定如下：

float dirLightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f };
float dirLightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float dirLightSpecular[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float dirLightDirection[3] = { 0.0f, 0.0f, -1.0f };

在已经有全局环境光的情况下，定向光的环境光分量看起来似乎是多余的。然而，当光源“开启”或“关闭”时，全局环境光和定向光的环境光分量的区别就很明显了。当“开启”时，总环境光分量将如预期的那样增加。上面的例子中，我们只使用了很小的环境光分量。在实际场景中，应当根据场景的需要平衡两个环境光分量。位置光在3D 场景中具有特定位置。靠近场景的光源，例如台灯，蜡烛等。像定向光一样，位置光的效果取决于撞击角度；但是，它没有方向，因为它对场景中的每个顶点的光照方向都不同。位置光还可以包含衰减因子，以模拟它们的强度随距离减小的程度。与我们看到的其他类型的光源一样，位置光具有指定为RGBA 值的环境光反射、漫反射和镜面反射特性。位置（5,2,−3）处的红色位置光可以指定如下例：

float posLightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f };
float posLightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float posLightSpecular[4] = { 1.0f,0.0f, 0.0f, 1.0f };
float posLightLocation[3] = { 5.0f, 2.0f, -3.0f };

衰减因子有多种建模方式。其中一种方式是使用恒定、线性和二次方（分别称为kc, kl和kq）衰减，并引入非负可调参数。这些参数与离光源的距离（d）结合进行计算：

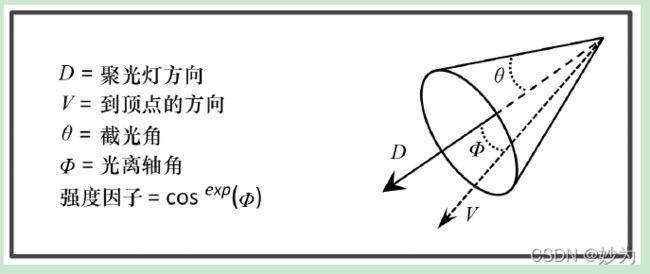
将这个因子与光的强度相乘可以使距光更远时，光的强度衰减更多。注意，kc 应当永远设置为大于等于1 的值，从而使得衰减因子落入[0…1]区间，并当d 增大时接近于0。聚光灯（spotlight）同时具有位置和方向。其“锥形”效果可以使用0°～90°的截光角θ来模拟，指定光束的半宽度，并使用衰减指数来模拟随光束角度的强度变化。如图7.2 所示，我们确定聚光灯方向与从聚光灯到像素的向量之间的角度φ。当φ 小于θ 时，我们通过将φ的余弦提高到衰减指数来计算强度因子（当φ 大于θ 时，强度因子设置为0）。结果是强度因子的范围为0～1。衰减指数会影响当角度φ 增加时，强度因子趋于0 的速率。然后将强度因子乘以光的强度以模拟锥形效果。

图二
位于（5,2,−3）向下照射Z 轴负方向的红色聚光灯可以表示为：

float spotLightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f };
float spotLightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float spotLightSpecular[4] = { 1.0f,0.0f, 0.0f, 1.0f };
float spotLightLocation[3] = { 5.0f, 2.0f, -3.0f };
float spotLightDirection[3] = { 0.0f, 0.0f, -1.0f };
float spotLightCutoff = 20.0f;
float spotLightExponent = 10.0f;

聚光灯也可以引入衰减因子。我们没有在上面的代码中展示它们，不过，聚光灯衰减因子可以用与前述定向光源相同的方式实现。历史上，自1986 年皮克斯的著名动画《小台灯》（Luxo Jr.）出现起，聚光灯就成为了计算机图形学的标志。当设计拥有许多光源的系统时，程序员应该考虑创建相应的类结构，如定义Light 类以及其子类GlobalAmbient、Directional、Positional 以及Spotlight。由于聚光灯同时具有定向光和位置光的特性，这里就值得使用C++的多继承能力，让Spotlight 类同时继承于实现位置光和定向光的类。在示例中，由于内容足够简单，因此我们在当前版本中没有加入这种层次结构。

材质

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。我们场景中物体的“外观”目前仅使用颜色和纹理进行表现。增加的光照使得我们可以加入表面的反射特性。即对象如何与我们的ADS 光照模型相互作用。这可以通过将每个对
象视为“由某种材质制成”来建模。通过指定4 个值（我们已经熟悉其中3 个值——环境光、漫反射和镜面RGB 颜色），可以在ADS 光照模型中模拟材质。第四种叫作光泽，正如我们将要看到的那样，它被用来为所选材质建立一个合适的镜面高光。目前许多不同类型的常见材质已经有ADS 和光泽度值了。例如，“锡镴”可以指定如下：

float pewterMatAmbient[4] = { .11f, .06f, .11f, 1.0f };
float pewterMatDiffuse[4] = { .43f, .47f, .54f, 1.0f };
float pewterMatSpecular[4] = { .33f, .33f, .52f, 1.0f };
float pewterMatShininess = 9.85f;

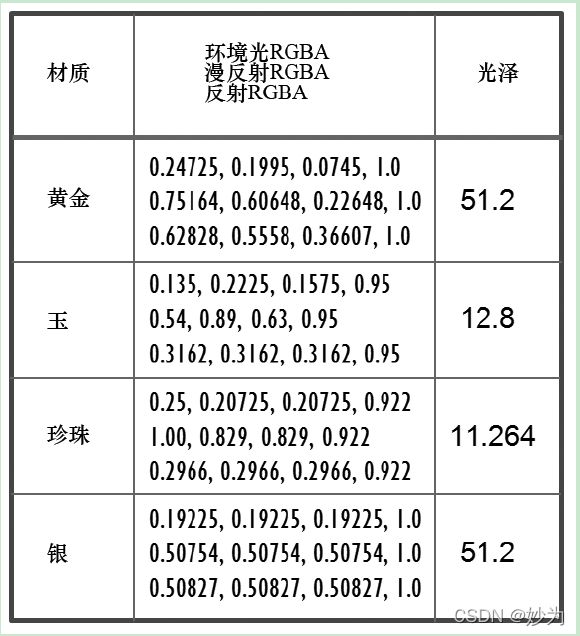
图三
一些其他材质的ADS RGBA 值见图三。有时候一些其他特性也属于材质特性。透明度由RGBA 标准中的第四个（alpha）通道的不透明度来实现。取值为1.0 是表示完全不透明，取值为0 时表示完全透明。对于大多数材质而言，只需要把不透明度设置为1.0就行了，但是对于某些特定的材质，加入一
些透明度是很重要的。例如，图7.3 中材质“玉”和“珍珠”都含有少量透明度（取值略微小于1.0）以显得更加真实。放射性有时也包含在ADS 材质规范中。在模拟自身发光的材质（例如磷光材质）时非常有用。
没有纹理的物体在渲染时，通常需要指定材质特性。因此，预定义一些可供选择的材质，在使用时会很方便。因此我们需要在Utils.cpp文件中添加如下代码：

// 黄金材质 — 环境光、漫反射、镜面反射和光泽
float * Utils::goldAmbient() { static float a[4] = { 0.2473f, 0.1995f, 0.0745f, 1 }; return
(float * ) a; }
float * Utils::goldDiffuse() { static float a[4] = { 0.7516f, 0.6065f, 0.2265f, 1 }; return
(float * ) a; }
float * Utils::goldSpecular() { static float a[4] = { 0.6283f, 0.5559f, 0.3661f, 1 }; return
(float * ) a; }
float Utils::goldShininess() { return 51.2f; }
// 白银材质 — 环境光、漫反射、镜面反射和光泽
float * Utils::silverAmbient() { static float a[4] = { 0.1923f, 0.1923f, 0.1923f, 1 }; return
(float * ) a; }
float * Utils::silverDiffuse() { static float a[4] = { 0.5075f, 0.5075f, 0.5075f, 1 }; return
(float * ) a; }
float * Utils::silverSpecular() { static float a[4] = { 0.5083f, 0.5083f, 0.5083f, 1 }; return
(float * ) a; }
float Utils::silverShininess() { return 51.2f; }
// 青铜材质 — 环境光、漫反射、镜面反射和光泽
float * Utils::bronzeAmbient() { static float a[4] = { 0.2125f, 0.1275f, 0.0540f, 1 }; return
(float * ) a; }
float * Utils::bronzeDiffuse() { static float a[4] = { 0.7140f, 0.4284f, 0.1814f, 1 }; return
(float * ) a; }
float * Utils::bronzeSpecular() { static float a[4] = { 0.3936f, 0.2719f, 0.1667f, 1 }; return
(float * ) a; }
float Utils::bronzeShininess() { return 25.6f; }

这样在init()函数中或全局中为物体指定“黄金”材质就非常容易了，如下所示。

float* matAmbient = Utils::goldAmbient();
float* matDiffuse = Util::goldDiffuse();
float* matSpecular = util.goldSpecular();
float matShininess = util.goldShininess();

注意，目前为止的各小节中，我们所用来实现的光照和材质特性的代码并没有引入光照。这些代码仅仅提供了用于描述并存储场景中元素所需光照和材质特性的一种方式。我们仍然需要自己计算光照。编写计算光照的代码需要在我们的着色器代码中引入一些严肃的数学过程。因此，让我们先来看看C++/OpenGL 和GLSL 图形程序中实现ADS 光照的基础。

ADS 光照计算

ADS 光照计算

当我们绘制场景时，每个顶点坐标都会进行变换以将3D 世界模拟到2D 屏幕上。每个
像素的颜色都是光栅化、纹理贴图以及插值的结果。现在我们需要加入一个新的步骤来调
整这些光栅化之后的像素颜色，以便反应场景中的光照和材质。我们需要做的基础ADS 计
算是确定每个像素的反射强度（Reflection Intensity，I）。计算过程如下：

我们需要计算每个光源对于每个像素的环境光反射、漫反射和镜面反射分量，并求和。当然，这些计算都基于场景内的光源类型以及渲染中模型的材质类型。环境光分量是最简单的。它的值是场景环境光与材质环境光分量的乘积：

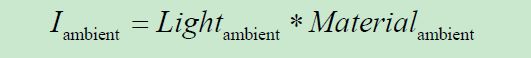
请记住光与材质亮度都是RGB 值，计算可以更准确地描述为：

漫反射分量会更复杂一些，因为它基于光对于平面的入射角。朗伯余弦定律（1760 年出版）确定了表面反射的光量与光入射角的余弦成正比。可以建模为如下公式：

与上面的计算相同，实际计算中所用到的是红、绿、蓝分量。确定入射角θ 需要（a）求解从所绘制向量到光源的向量（或者与光照方向相反的向量），（b）求解所渲染物体表面的法（垂直）向量。让我们将其分别称为L 和N，如图四 所示。基于场景中光的物理特性，向量L 可以通过对光照方向向量取反，或通过计算像素位置到光源位置的向量得到。计算向量N 会麻烦一些——法向量有可能已经在模型中给出了，但是如果模型没有给出法向量N，那么就需要基于周围顶点位置，在几何上对向量N 进行估计。在本章剩下的内容中，我们假设所渲染的模型每个顶点都包含法向量（使用建模工具如MAYA
或Blender 创建的模型，通常都包含法向量）。事实上，在计算法向量时，没必要计算出θ 角本身的角度。我们真正需要的是cos(θ)。这可以通过点乘计算得出。因此，漫反射分量可以通过如下公式得出：

图四

漫反射分量仅当表面暴露在光照中时起作用，即当−90 < θ < 90，cos(θ) > 0 时。因此，
我们需要将之前等式的最右项替换为：

镜面反射分量决定所渲染的像素是否需要作为“镜面高光”的一部分变亮。它不止与光源的入射角相关，也与光在表面上的反射角以及观察点与反光表面之间的夹角相关。在图五 中，R 代表光反射的方向，V（叫作观察向量view vector）是从像素到眼睛的向量。注意，V 是对从眼睛到像素的向量取反（在相机空间中，眼睛位于原点）。在R 与V 之间的小夹角φ 越小，眼睛越靠近光轴，或者说看向反射光，因此像素的镜面高光分量也就越大（像素看来应该更亮）。φ 用于计算镜面反射分量的方式取决于所渲染物体的“光泽度”。极端闪亮的物体，如镜子，其镜面高光非常小——它们将入射的光直接反射给了眼睛。不那么闪亮的物体，其镜面高光会扩散开来，因此高光会包含更多的像素。反光度通常用衰减函数来建模，这个衰减函数用来表达随着角度φ 的增大，镜面反射分量降低到0 的速度。我们可以用cos(φ)来对衰减进行建模，通过余弦函数的乘方来增减反光度，如cos(φ), cos2(φ), cos3(φ), cos10(φ), cos50(φ)等，如图六 所示。

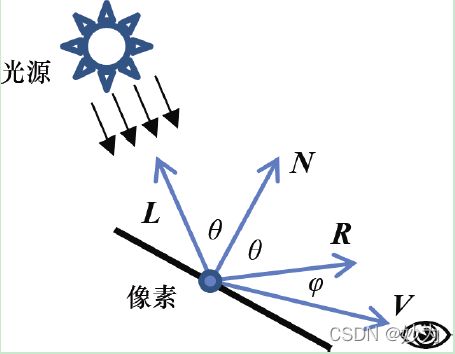
图五

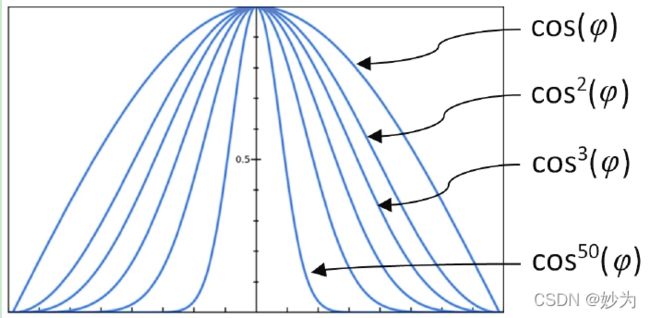
图六

注意，指数中的阶数越高，衰减越快，因此在视角光轴外的反光像素镜面反射分量越小。我们将衰减函数cosn(φ)中的指数n 叫作材质的反光度因子。注意在之前的图7.3 中，每个材质的反光度因子在最右列给出。现在我们可以给出完整的镜面反射计算：

注意，与之前计算漫反射一样，我们使用了max()函数。在本例中，我们需要确保镜面反射分量不使用cos(φ)所产生的负值，如果使用了负值，则会有奇怪的伪影，如“暗”镜面高光。同时，如之前一样，真正的计算中包含了红、绿、蓝3 个分量。

参考

计算机图形学编程（使用OpenGL和C ）