经典算法-----八皇后问题

 目录

前言

八皇后问题

1.问题简介

1.2思路剖析

1.3递归和回溯

代码实现

​编辑

1.递归回溯解决

能否放置数组

完整代码：

2.非递归回溯解决

---

前言

        今天我们学习一个新的算法，也就是回溯算法，就以八皇后问题作为示例，这是一个非常有意思的问题，下面就一起来看看吧。

八皇后问题

1.问题简介

八皇后问题（英文：Eight queens），是由国际象棋棋手马克斯·贝瑟尔于1848年提出的问题，是回溯算法的典型案例。

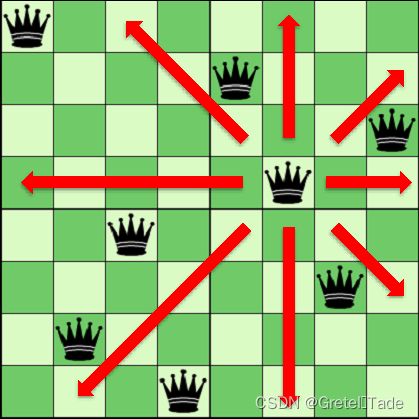
        问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

        高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转，和对角线对称变换的摆法看成一类，共有42类。计算机发明后，有多种计算机语言可以编程解决此问题。

看完这个问题描述之后，看上去好像很简单的样子，不就是去摆放棋子嘛，但是当你用编程去写的话就是另外一码事了，压根就不知道从哪里下手。 

1.2思路剖析

还记得在此之前我发布了一个关于迷宫问题的解法吗？（链接：经典算法-----迷宫问题（栈的应用）-CSDN博客）对于迷宫问题是利用栈的回溯算法解决的，当走到死路的时候就往回走，回到上一个位置换一个方向来走，那摆放皇后也是一样的，当下一个无法摆放的时候，那就回到上一个，然后重新摆放上一个皇后再去看看下一个能不能摆放，如果还是不能摆放的话，那就回到上上一个，直到回到第一个皇后，全部重新摆放……

1.3递归和回溯

递归

对于递归算法，我觉得掌握递归是入门数据结构与算法的关键，因为后面学习很多操作涉及到递归，例如链表的一些操作、树的遍历和一些操作、图的dfs、快排、归并排序等等。

而递归的主要特点如下：

• 自己调用自己
• 递归通常不在意具体操作，只关心初始条件和上下层的变化关系。
• 递归函数需要有临界停止点，即递归不能无限制的执行下去。通常这个点为必须经过的一个数。
• 递归可以被栈替代。有些递归可以优化。比如遇到重复性的可以借助空间内存记录而减少递归的次数

回溯 

算法界中，有五大常用算法：贪心算法、分治算法、动态规划算法、回溯算法、分支界限算法。回溯算法是五大算法之一，虽然有时候复杂度回挺高的，但是回溯算法可以简化去解决很多问题，就向处理套娃问题一样，如果让人去想那就太费脑子了，如果直接去通过递归回溯那计算机回很快解决出来。前面说到的递归，本身来看好像跟八皇后问题的解决没有太大的关系，但是加上回溯就是不一样啦。下面看代码分析吧 

代码实现

 既然都知道了解决算法思路，那我也不装了，直接上代码！！！！！！

1.递归回溯解决

能否放置数组

问题来了，怎么去看这个位置能不能放皇后呢？这里就需要几个标致数组去解决，如下所示：

#define num 8 //定义皇后的数量

int* place = (int*)malloc(sizeof(int) * num);//这个表示是放置皇后的标志
int* y_flag = (int*)malloc(sizeof(int) * num);//这个数组是表示放了皇后之后此时的纵列是能否可以放皇后的标志
int* d1 = (int*)malloc(sizeof(int) * (2 * num - 1));//这个是表示放皇后之后的上对角线能否放的标志
int* d2 = (int*)malloc(sizeof(int) * (2 * num - 1));//这个是表示放皇后后下对角线能否放皇后的标志
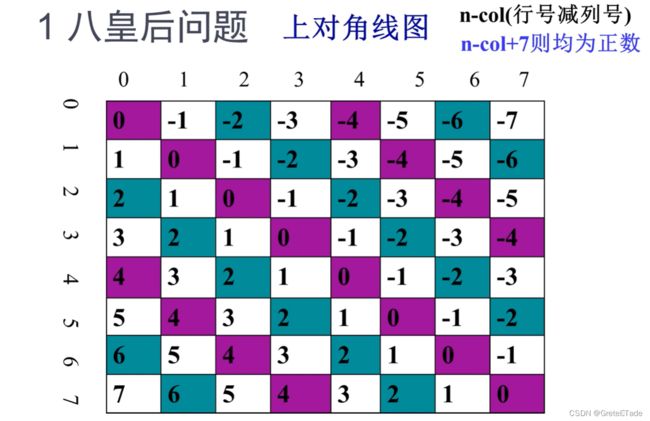
//以上的标志数组，其中1表示可以放，0表示不可以放

对于上对角线d1，我们可以去通过这个位置的行位置（第n行）来减掉当前的纵位置（第col列），得到的结果如下图所示，问题来了，我数组的下标不可以是负数呀，所以我们可以在这个前提下加上当前的棋盘长度（长度为num），公式为：n-col+num，最后得到的结果就是下标为0~14的数组啦。

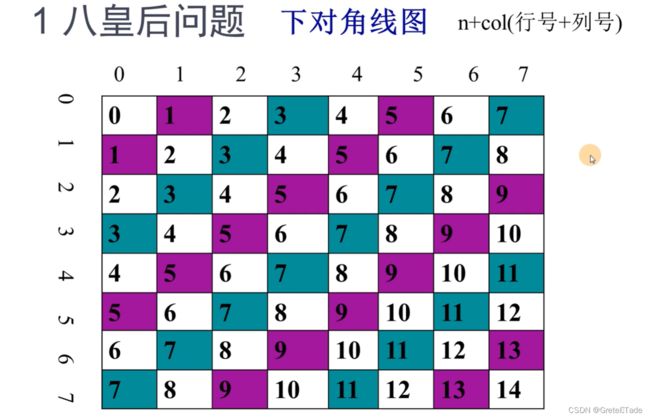
说完了上对角线d1，那就来说下对角线d2 ，对于d2，我们可以这样子去处理，用行位置（n）和纵位置（col）的和就会得到如下图所示的结果，公式为：n+col

完整代码：

#include
#include
#include
#define num 8 //定义皇后的数量

int* place = (int*)malloc(sizeof(int) * num);//这个表示是放置皇后的标志
int* y_flag = (int*)malloc(sizeof(int) * num);//这个数组是表示放了皇后之后此时的纵列是能否可以放皇后的标志
int* d1 = (int*)malloc(sizeof(int) * (2 * num - 1));//这个是表示放皇后之后的上对角线能否放的标志
int* d2 = (int*)malloc(sizeof(int) * (2 * num - 1));//这个是表示放皇后后下对角线能否放皇后的标志
//以上的标志数组，其中1表示可以放，0表示不可以放

//如果放满了就进行打印
void print(int *count) {
	*count+=1;//统计次数
	printf("第%d次：\n", *count);
	for (int x = 0; x < num; x++) {
		for (int y = 0; y < num; y++) {
			if (place[x] == y)
				printf("Q");
			printf("#");
		}
		printf("\n");
	}
	printf("\n");
}

//执行函数
void generate(int n,int *count) {
	//每一个皇后有8种放置方法
	for (int col = 0; col < num; col++) {
		//如果可以放置的话，那就是这个位置的纵向为1，上对角线和下对角线也为1，就是可以放置
		if (y_flag[col] && d1[n - col + 7] && d2[n + col]) {
			//可以放置的话，那么这4个标志数组就宣告这个位置被占领了
			place[n] = col;
			y_flag[col] = 0;//定义为0，就是这个位置不能放了
			d1[n - col + 7] = 0;
			d2[n + col] = 0;
			//如果没有放完，就进行递归放下一个
			if (n < num-1)
				generate(n + 1,count);
			//如果放完了，那就打印这个结果
			else
				print(count);
			//放完之后就进行回溯，把当前皇后的位置抹除
			place[n] = 0;
			y_flag[col] = 1;
			d1[n - col + 7] = 1;
			d2[n + col] = 1;
		}
	}
}

int main() {
	//标志数组初始化
	memset(place, 0, sizeof(place));
	memset(y_flag, 1, sizeof(y_flag));
	memset(d1, 1, sizeof(d1));
	memset(d2, 1, sizeof(d2));
	
	int count = 0;//统计
	generate(0,&count);
}

2.非递归回溯解决

#include
#include
#include
//打印结果
void print(int* count,int* place,int num) {
	*count += 1;
	printf("第%d种：\n", *count);
	for (int i = 0; i < num; i++) {
		for (int j = 0; j < num; j++) {
			if (place[i] == j)
				printf("□");
			else
				printf("■");
		}
		puts("");
	}
	puts("");
}

void generate(int num,int *count,int* place,int *flag,int *d1,int *d2) {
	int n = 0;
	int col = 0;
	while (1)
	{
		for (; col < num; col++) {
			//如果可以放置，就宣告占领这个位置，然后结束这个循环，进入到下一层
			if (flag[col] && d1[n - col + 7] && d2[n + col]) {
				place[n] = col;
				flag[col] = 0;
				d1[n - col + 7] = 0;
				d2[n + col] = 0;
				break;
			}
		}
		//如果找到了放置的位置col < num
		if (col < num) {
			//如果没有放完，那就进入到放下一层
			if (n < num - 1) {
				col = 0;
				n++;
				continue;
			}
			//如果放完了，那就打印操作
			else
				print(count, place, num);
		}
		//回溯到上一层
		else {
			n--;
			col = place[n];
		}
		//抹除操作
		place[n] = 0;
		flag[col] = 1;
		d1[n - col + 7] = 1;
		d2[n + col] = 1;
		col++;
		//回溯到不能回溯为止，退出结束循环
		if (n == 0 && col == num)
			break;
	}
}

int main() {
	int num;
	int count = 0;//统计
	printf("输入要放的皇后：");
	scanf("%d", &num);
	//空间开辟，初始化
	int* place = (int*)malloc(sizeof(int) * num);
	int* flag = (int*)malloc(sizeof(int) * num);
	int* d1 = (int*)malloc(sizeof(int) * (2 * num - 1));
	int* d2 = (int*)malloc(sizeof(int) * (2 * num - 1));
	memset(place, 0, sizeof(int)*num);
	memset(flag, 1, sizeof(int)*num);
	memset(d1, 1, sizeof(int)* (2 * num - 1));
	memset(d2, 1, sizeof(int)* (2 * num - 1));

	generate(num,&count, place,flag,d1,d2);
}

运行结果：

以上就是这个问题的解决方法了，你们同样的可以去试一下用数据结构栈来解决这个问题，我就不多说了哈，你们学会了吗？

分享一张壁纸：