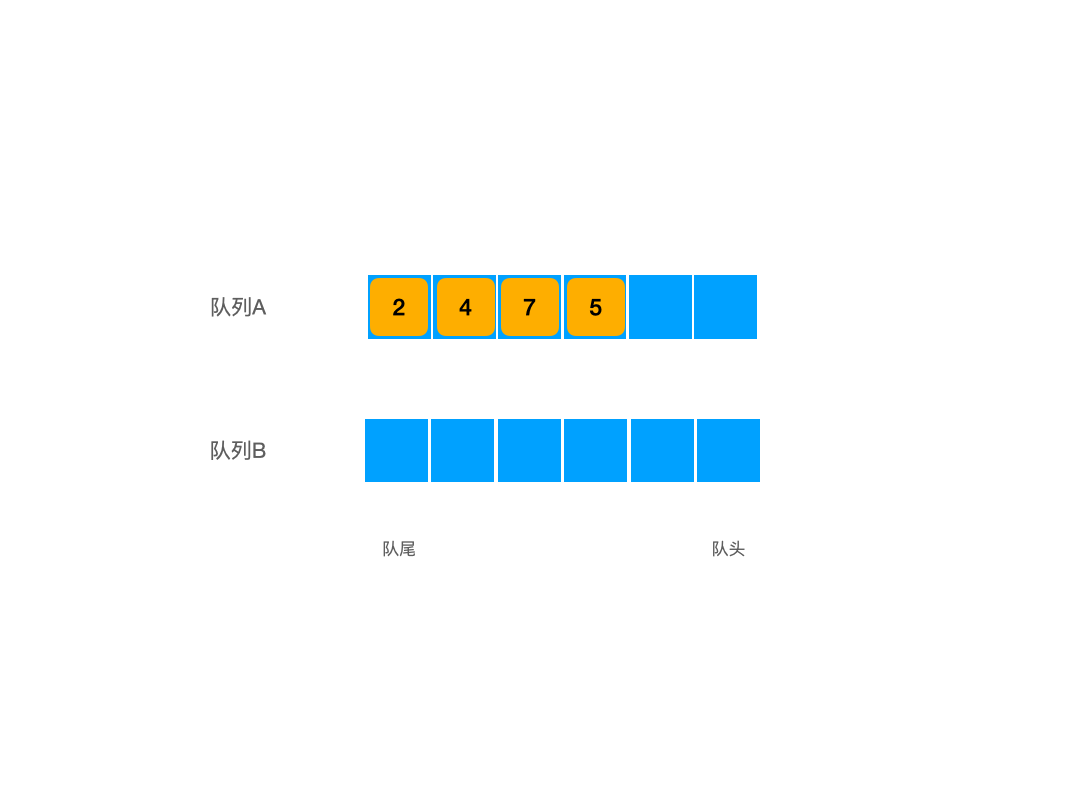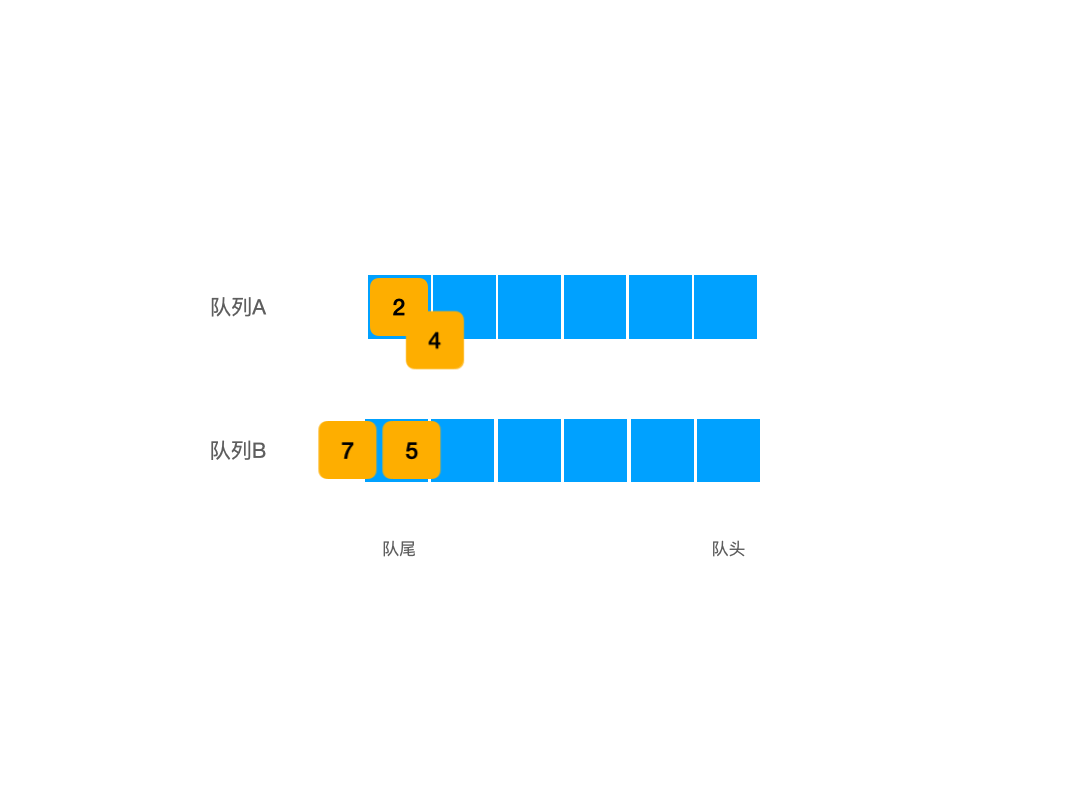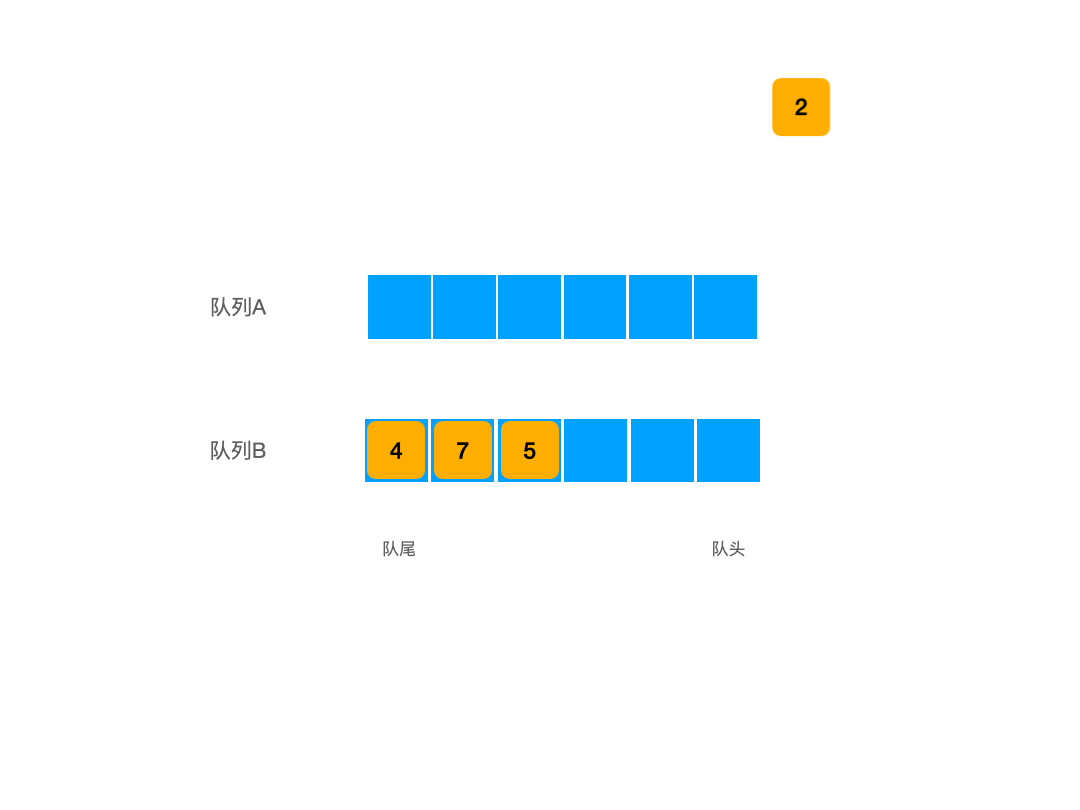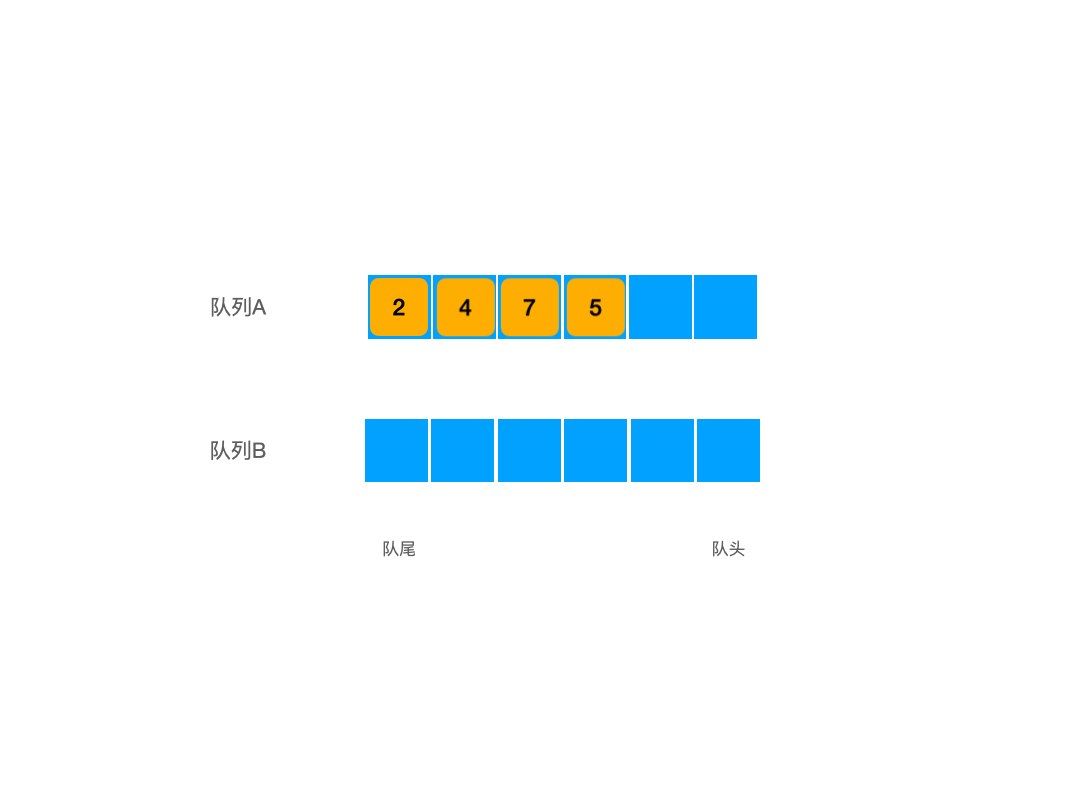栈和队列经典算法 —— 双栈实现队列与双队列实现栈
栈和队列经典算法 —— 双栈实现队列与双队列实现栈
摘要:栈和队列是数据结构中经典且重要的两个成员,我们在学习完线性表之后接触的最早两个数据结构就是这两个,关于这两个数据结构的算法也是非常多且重要,最重要的是这两个算法 —— 两个栈实现一个队列和两个队列实现一个栈。
文章目录
- 栈和队列经典算法 —— 双栈实现队列与双队列实现栈
-
- 1.栈和队列
- 2.两个栈实现一个队列
- 3.两个队列实现一个栈
1.栈和队列
想要学习这两个算法,首先要了解栈和队列的基础特性。栈和队列本质上是两种操作受限的线性表,其中栈是被限制成只能在其中一端做添加和删除操作,而队列则是被限制为只能在其中一端做添加,在另外一端做删除操作。接下来我们画图来看栈和队列的特性:
1.栈
栈是将线性表的添加删除位置限制在了一段的数据结构,也就说栈的添加和删除只能是在其中一段进行,这样一来这个操作受限的线性表就会像一个桶一样,先进入的数据就会被堵在最下边,只有上边的数据出去之后它才能出去,也就是说在栈中的数据是先入后出,如下图所示是栈的示意图:
2.队列
队列的理论流程如图所示,在队列队尾可以添加数据,在队头进行出队操作,其数据在队中的理论移动过程就是图中所示的样子。
当然我们在使用数组或者链表实际操作队列的时候并不是这样的,在真正的队列操作中其操作过程如下,我们通过两个指针来表示队头和队尾,我们永远在队尾进行添加操作,在队头进行删除操作,我们每在队尾添加一个,队尾指针就要后移,而我们每在队头删除一个,队头指针也要后移,知道两个指针相遇,我们认为队列清空了:
如上图所示,在队列中的数据是先入先出的,和我们日常生活中的排队状况一模一样。
我们了解了栈和队列的特性之后,就可以尝试书写下面的算法了,因为下面的两个算法本质上就是通过两种数据结构的特性进行相互转化,进而让两个栈实现一个队列,两个队列实现一个栈的功能。
2.两个栈实现一个队列
使用两个栈实现一个队列的原理是使用两个先入后出的栈结构模拟出一个先入先出的队列结构,我们只需明白栈结构是先入后出,而队列结构是先入先出,然后想办法使用两个栈模拟出这个过程即可。关于这个过程我们怎么模拟呢?我们使用图片来分析。
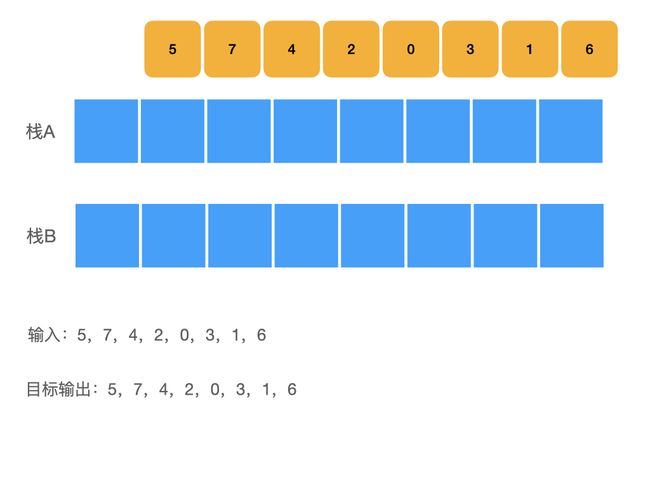
初始状态
如图所示,我们希望使用两个栈实现一个队列,我们的目标输入是5,7,4,2,0,3,1,6,输入之后我们再一次性输出,如果是队列的话,我们的输出应该也是5,7,4,2,0,3,1,6,但是我们现在只有两个栈,使用栈来进行这个输入的话,我们的输出是6,1,3,0,2,4,7,5,这肯定是不符合我们的需求的,我们现在想要实现的目标,就是使用先入后出的栈来实现先入先出的队列,我们要保证先进入系统的元素要能够被先输出,为了实现这个效果,我们应该进行如下的操作限制。
入队状态
首先我们在入队时,就是正常的往栈A中压栈,此时就是正常的压栈操作,如图:
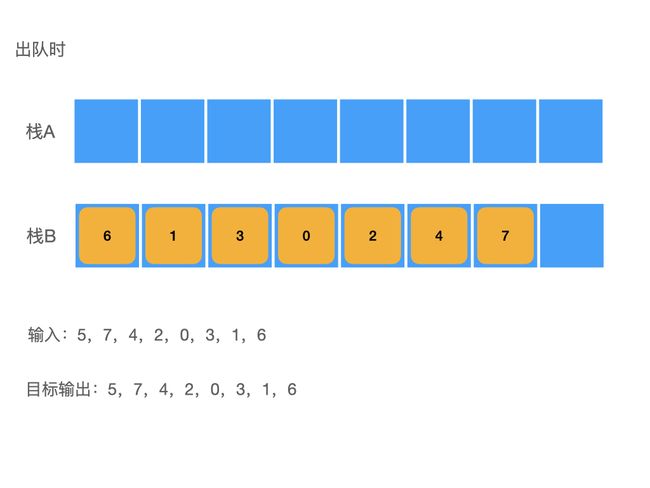
出队状态
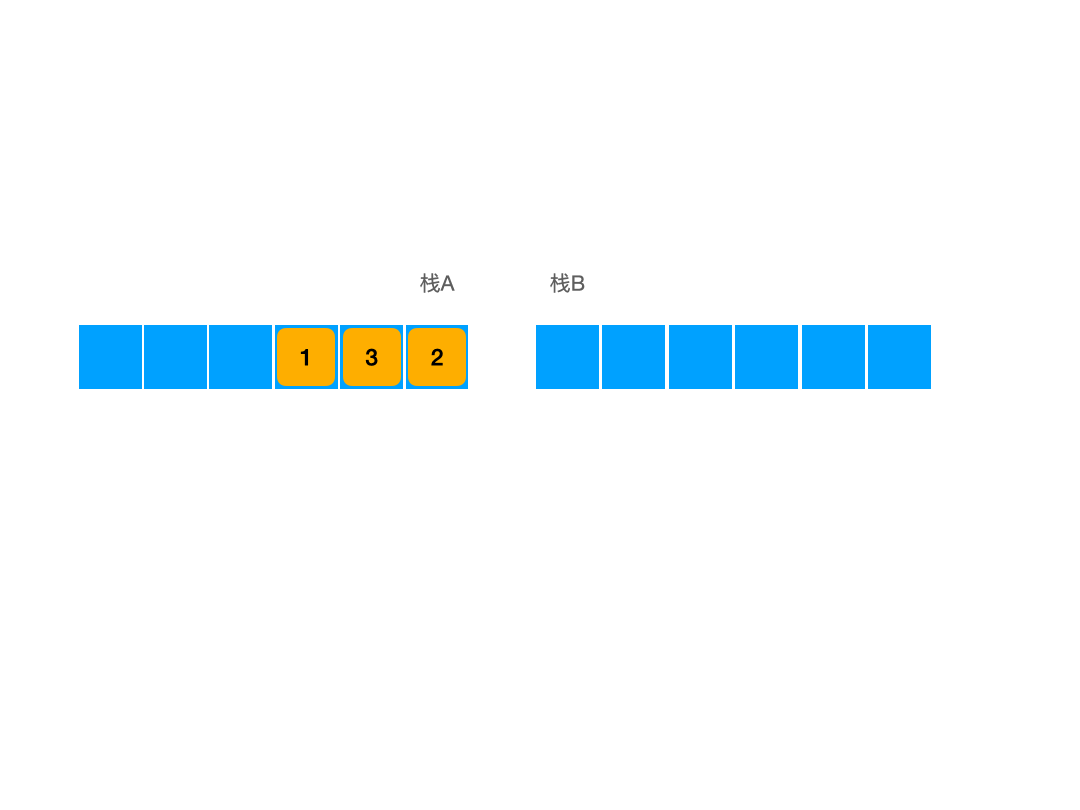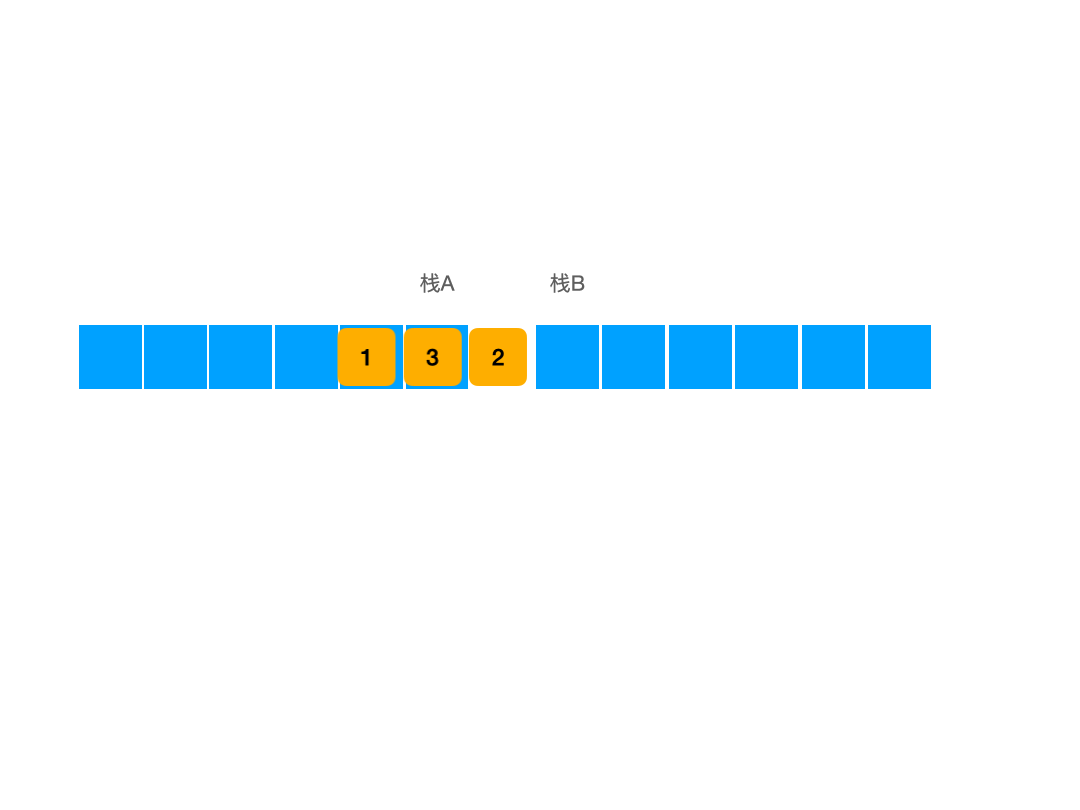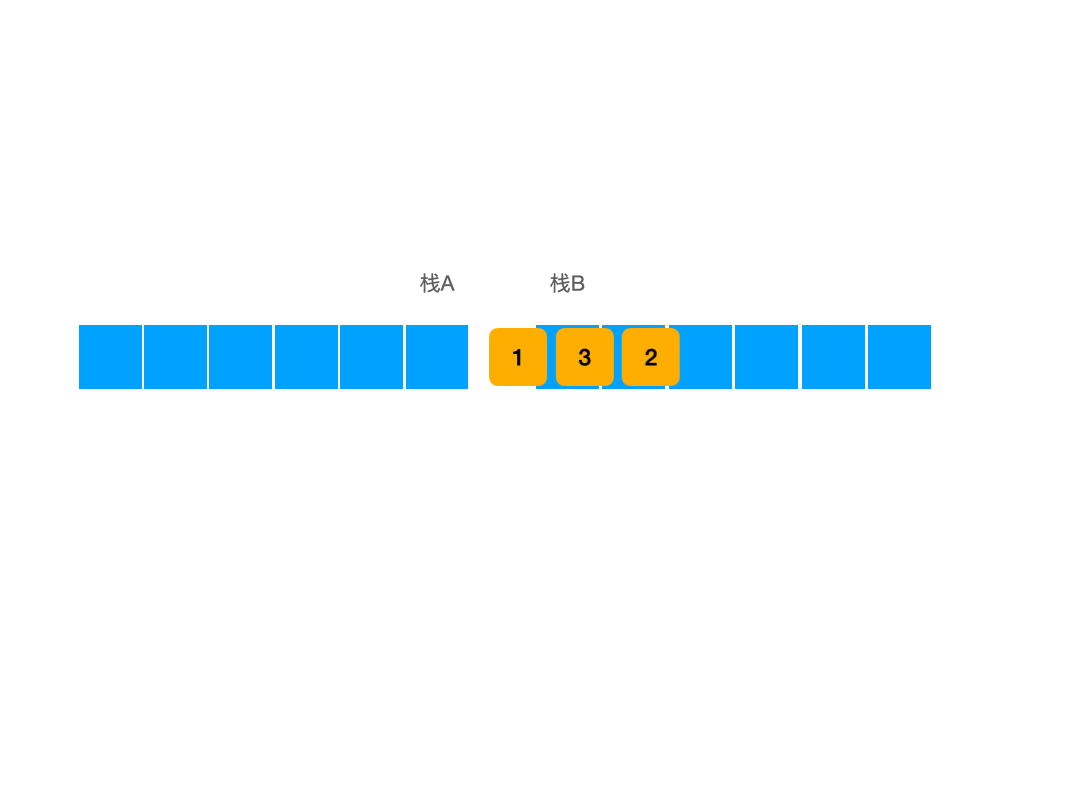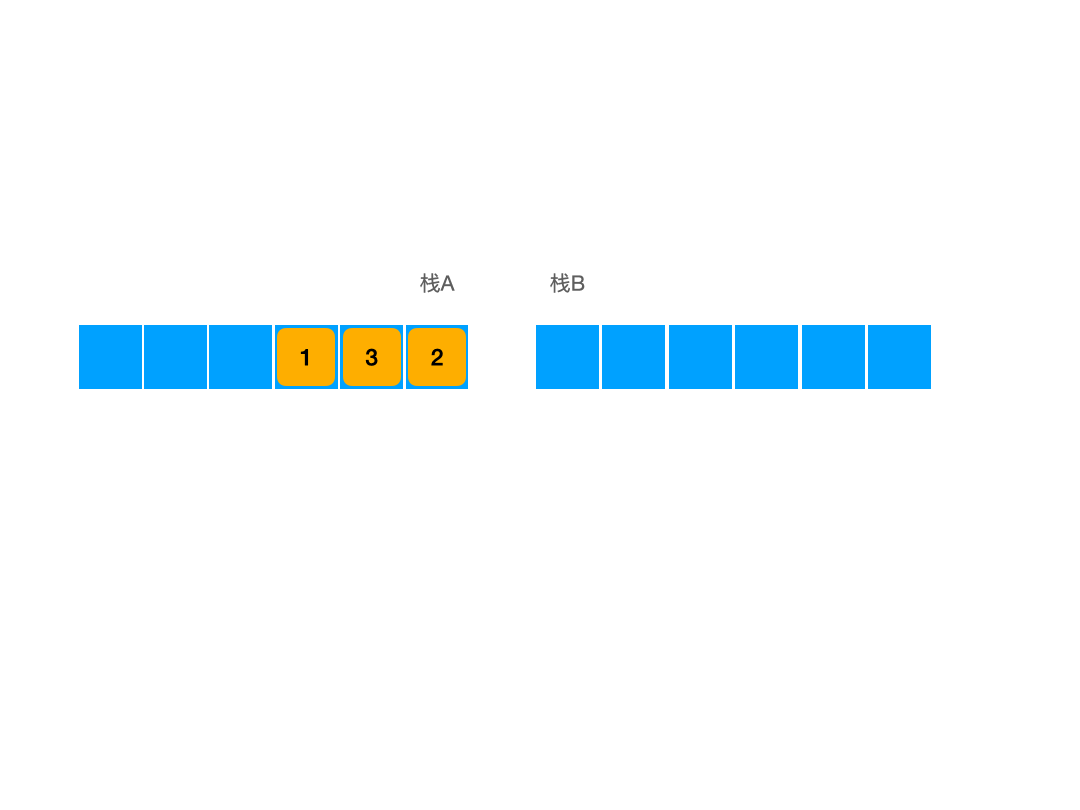
而在出队的时候,我们就不能像往常一样直接出栈了,我们这时需要使用到栈B进行暂存,因为我们如果直接使用栈的出栈方法出栈的话,那我们的输出顺序必然是错的,此时我们为了实现队列的输出效果,必须将最先入栈的元素之后入栈的元素都弹出栈,我们才能访问到最先入栈的那个元素,然后我们将其出栈,才能实现先入先出,如图所示:
这样一来我们就能够在没有出队其他元素的状态下弹出我们最新先入队的元素了,此时此刻最先入队之后入队的元素并没有丢失,它们被暂存在栈B中,在当前样例下,栈B的状态为:
根据这个状态我们可以发现,当我们将栈A中的东西倒入到栈B中之后,其序列顺序会发生反转,此时先入队的元素们会成为栈顶,而后入队的元素们此时则成为了栈低,也就是说如果此时我们不再做任何入队操作,只做出队操作的话,直接对栈B进行出栈操作,其最终的出栈顺序就已经符合我们的目标输出了。
这时有些人基于惯性思维可能会这样想:我们在进行完一次输出之后,还有没有必要将栈B中的元素在压入回栈A中呢?因为我们想在还原A栈的状态之后,继续入队,然后重复出栈的过程,这样一来可以保证万无一失的先入先出。首先这个思路肯定是可以的,但实际上是没必要的,因此此时我们即使是直接在栈A中入栈,也是可以保证先入先出的,这是因为即使此时我们将栈B中的元素输回去,然后在栈A中入栈,然后再进行出队操作,出队的顺序也不会发生改变,所以此时我们没有必要进行这种操作。
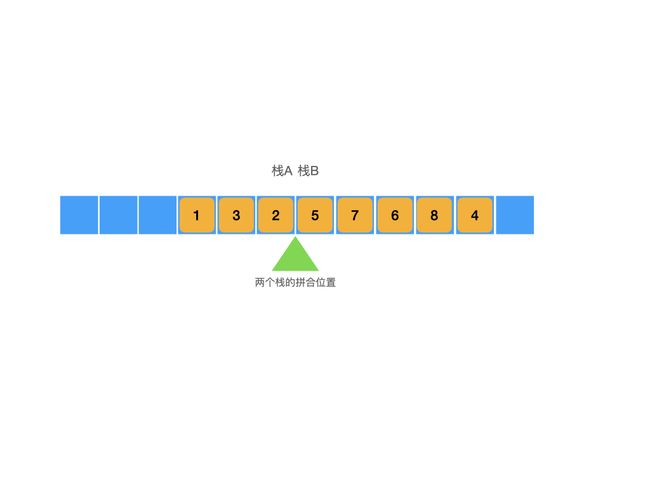
因此在这个算法中我们想要入栈的话,就直接向栈A中直接入栈,而出栈的时候我们就直接从栈B中出栈,当B中为空的时候,我们就要从栈A中导入一次元素了,这样一来我们就成功实现了先入先出的方法。实际上我们可以将这个过程理解为将两个栈栈底相对的拼在一起,一边的栈顶专门入栈,另一边的栈顶专门出栈,而因为两栈相对,栈A中的元素本身就是和栈A中的元素相反的,而两栈之间的元素互导会导致元素再次相反一次,进而导致逻辑上这些元素的顺序并没有相反,而是直接从A栈平移到了B栈,进而两个栈拼合成了一个队列。现在我们用图片来展示一下这个逻辑过程:
最终的拼合结果是这样的:
其中两个栈的栈底是相邻的,而栈顶则是指向相反位置,如图所示:
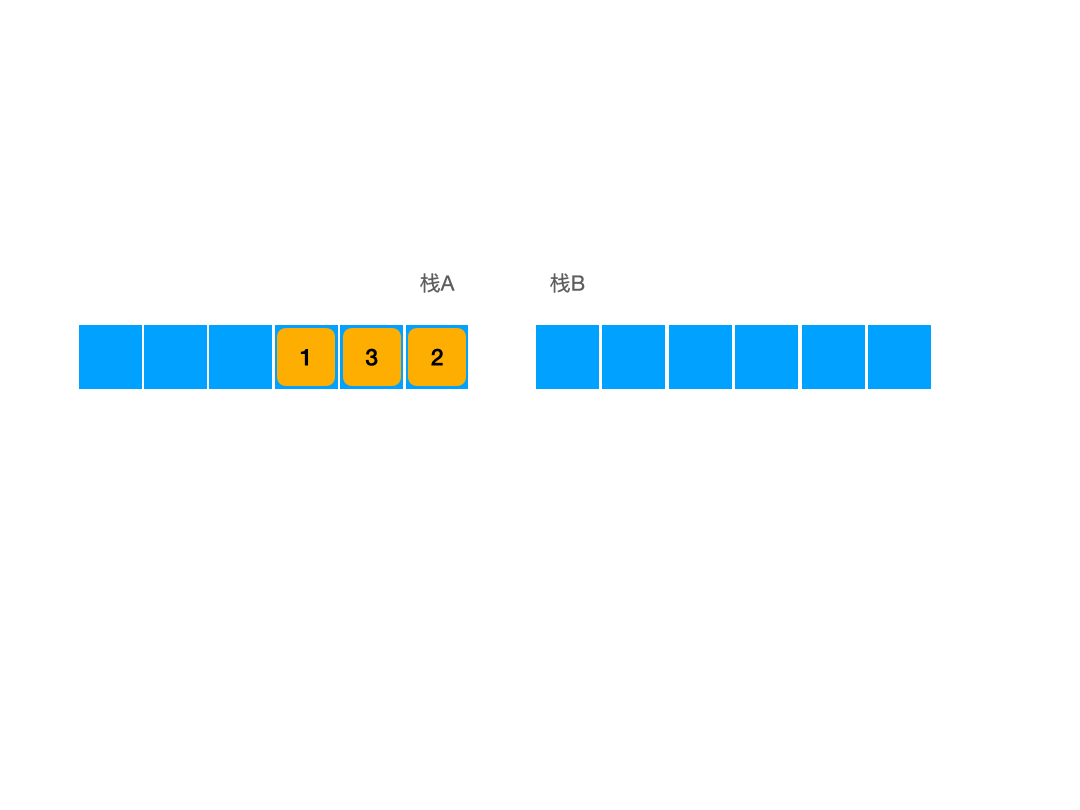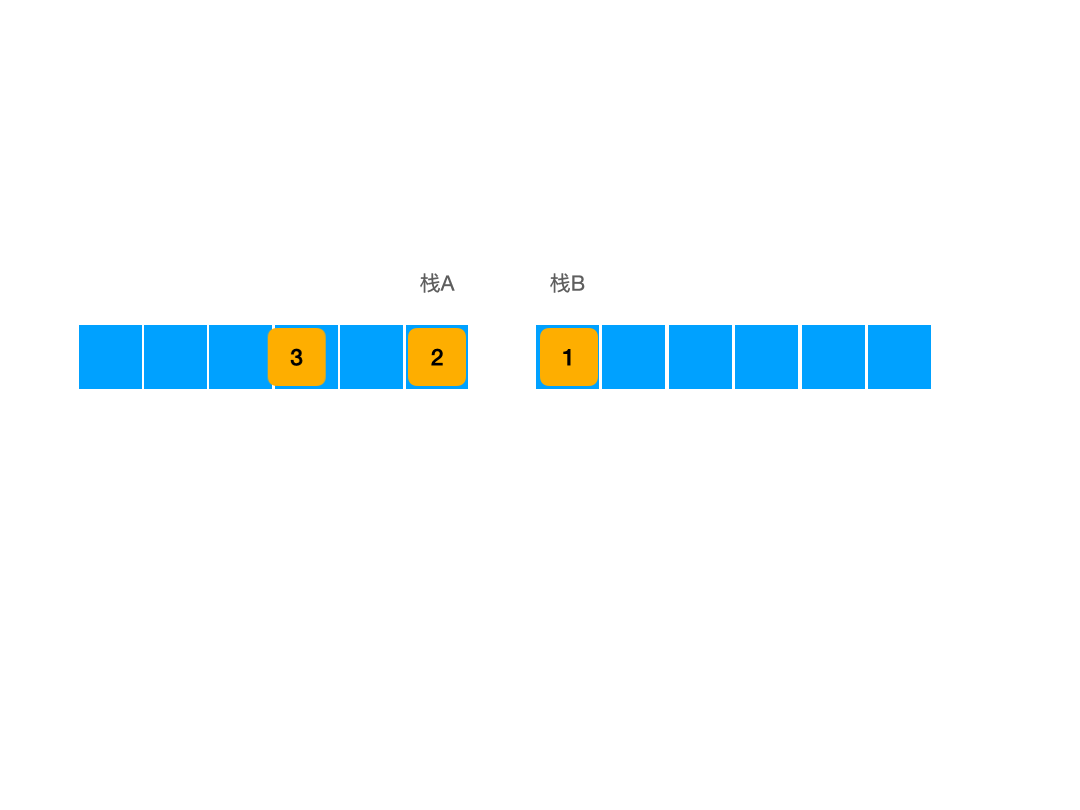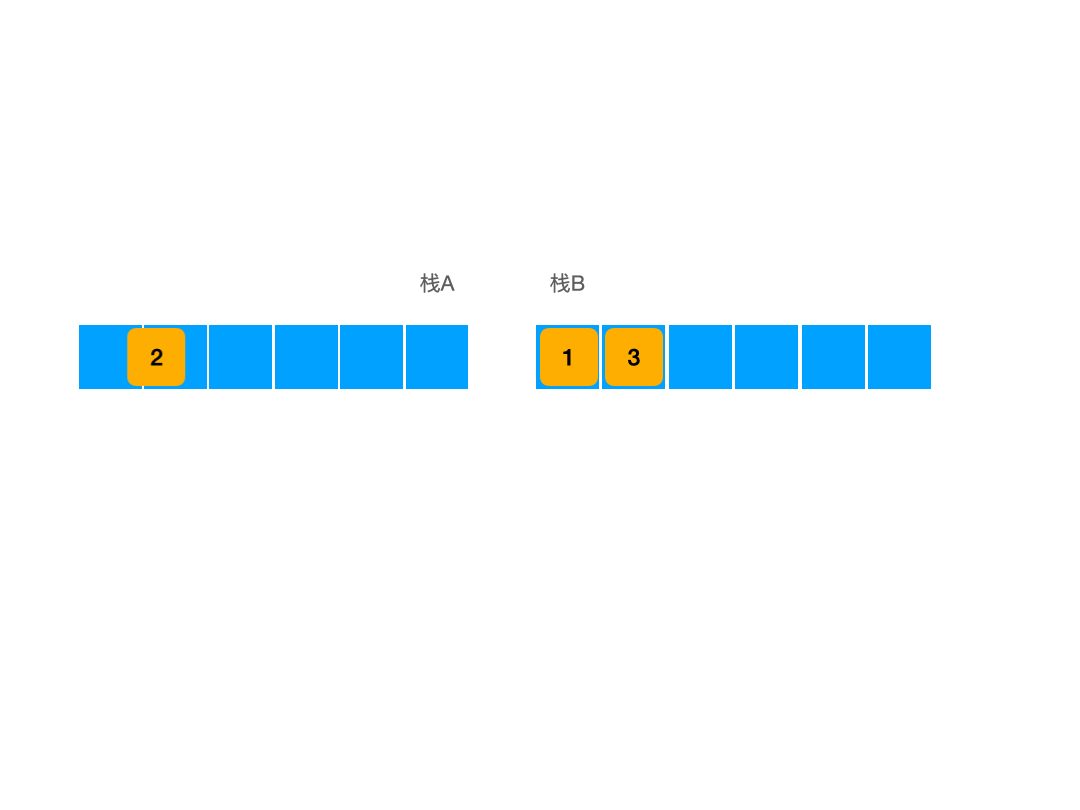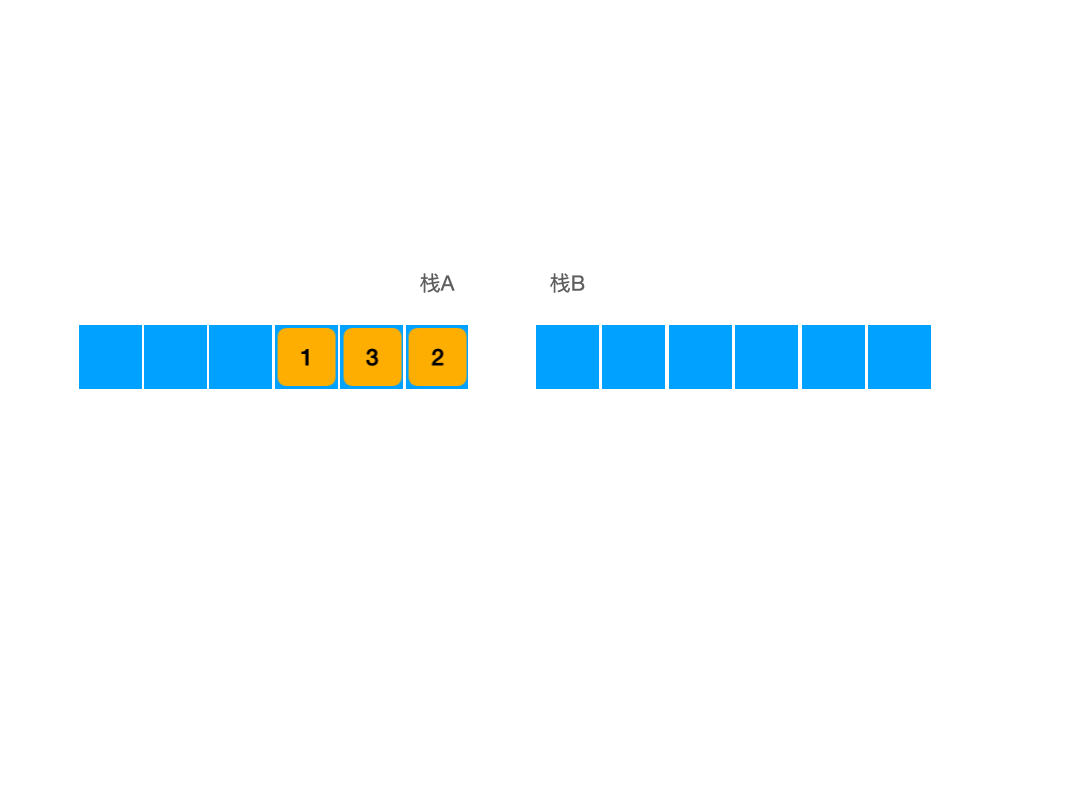
此时我们发现栈A还是那个栈A,但是逻辑上它里边的元素实际上和栈B中的元素的正方向相反了,而栈的相互导入会导致方向变换,所以从栈A中向栈B中按规则导入元素,实际上相当于在上图中直接将元素向右平移,因此我们实际上不必将栈B中的元素再放回来,而是直接在栈A中加入元素,当出栈的时候直接在栈B中出栈,而当栈B中没有元素时再从栈A中向B中导入元素即可,这里我们必须在栈B中没有元素之后才能导入,因为栈的规则,这种类似平移的行为只有在B栈中为空的时候才是合乎逻辑的,如图:
使用栈的理解方式转移元素
我们看,其最终结果是不是和直接平移是一样的:
而当栈B中有元素时,A栈中导出的元素会直接排列在B栈中已有元素的后边,而无法形成逻辑上的平移效果,因此我们最终确定算法为:在入队时,我们直接在栈A中入队;在出队时,我们首先检测栈B中有无元素,如果栈B中有元素的话那么就直接对栈B进行出栈操作,如果B栈中为空的话,我们首先要将A栈中的元素全数导出到栈B中,然后再对栈B出栈。
我们现在来实现一下这个算法:
import java.util.Stack;
public class TwoStackQueue {
Stack<Integer> stackA = new Stack<>();
Stack<Integer> stackB = new Stack<>();
public void push(Integer num){
stackA.push(num);
}
public int pop(){
Integer re = null;
if(!stackB.empty()){
re = stackB.pop();
}else {
while (!stackA.empty()) {
re = stackA.pop();
stackB.push(re);
}
if(!stackB.empty()){
re = stackB.pop();
}
}
return re;
}
}
3.两个队列实现一个栈
接下来我们尝试理解使用两个队列实现一个栈的方法。我们已经知道队列的特点是先进先出,而我们希望通过先进先出的队列制作出一个先进后出的栈来。在这个算法中,用户输入5,4,3,2这些数据之后,希望得到一个2,3,4,5的输出,这是因为栈是先进后出的,但是我们现在只有两个队列,队列是先进先出的,不符合我们的需求,我们应该怎么办?这个过程我们使用图片来解释:
首先我们让元素在A队列中入栈:
当整体出栈时,我们先让A队列中的元素出队,但是不输出,而是先存放到B队列中去,而当我们出队出到队列中最后一个时,我们不再将其入队,而是将其直接输出:
这样一来我们就将队列中最新加入的先输出出来了,进而实现了先进先出。在队列实现栈中,我们无法向上一个算法中一直在一个表中存放数据,我们在使用完B队列之后,必须立刻将B队列里的元素们放回去:
之后我们继续向队列A中输入数据,然后重复出栈入栈操作。
综上所述,使用队列实现栈的思路比较简单,总体上就是:入栈时将元素向A队列中添加元素,在出栈时我们使用队列B当做辅助队列,临时暂存我们队列A中的元素,我们让队列A不断的向B中注入元素,然后当队列A中只剩下一个元素的时候,它就是我们最新输入的元素,这时我们再直接输出它即可;之后我们要将辅助队列B中的元素全部再放回到A中,以便保证下次输入的逻辑依然正确。这是因为队列是两端都可以进行操作的数据结构,我们无法像*“栈实现队列”*的算法一样进行两个线性表拼合,我们只能是通过一个暂存区为其加限制,进而让其展现出栈的特性,我们在这里如果不把B队列中的元素清空,就无法正确的得到下次的出栈元素,因为此时队列B的结构和队列A的结构是一样的,而A队列中此时又已经有数据了,我们无法通过单个的队列B来直接输出其最新加入的数据,且因为这时A队列不空了,我们不能将其作为辅助队列了,因为这时如果再向队列A中加入元素的话,就会直接导致算法中的一个最新输入变成最早的输入,进而直接破坏整个算法的逻辑,因此我们必须将队列B全部移动到队列A中,恢复之前的状态,然后再进行新的操作。
现在我们实现一个这个算法:
import java.util.LinkedList;
import java.util.Queue;
public class TwoQueueStack {
Queue<Integer> queueA = new LinkedList<>();
Queue<Integer> queueB = new LinkedList<>();
public void push(Integer value){
queueA.offer(value);
}
public int pop(){
Integer data = null;
while (!queueA.isEmpty()){
data = queueA.poll();
if(queueA.isEmpty()){
break;
}
queueB.offer(data);
}
while (!queueB.isEmpty()){
queueA.offer(queueB.poll());
}
return data;
}
}