队列--环形数组实现
具体代码可参考:https://github.com/1693905917/DataStructure.git
好处
对比普通数组,起点和终点更为自由,不用考虑数据移动
“环”意味着不会存在【越界】问题
数组性能更佳
环形数组比较适合实现有界队列、RingBuffer 等
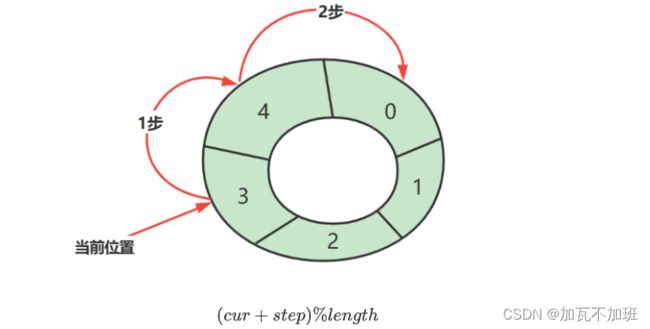
下标计算
例如,数组长度是 5,当前位置是 3 ,向前走 2 步,此时下标为 (3 + 2)\%5 = 0
cur 当前指针位置
step 前进步数
length 数组长度
注意:
-
如果 step = 1,也就是一次走一步,可以在 >= length 时重置为 0 即可
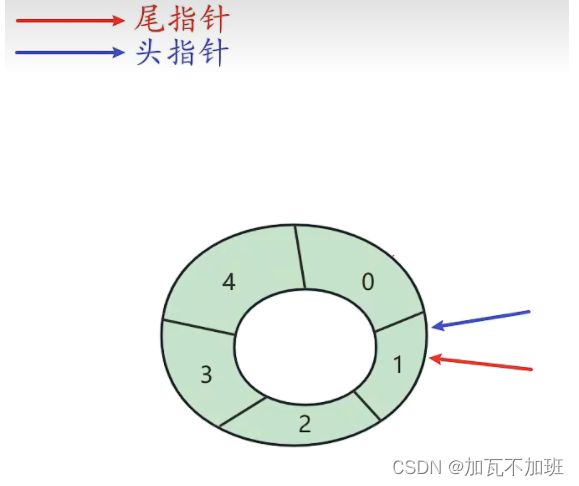
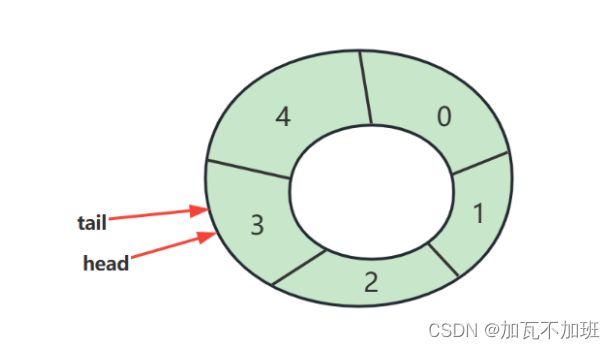
判断空
判断该数组是否为空:头指针==尾指针
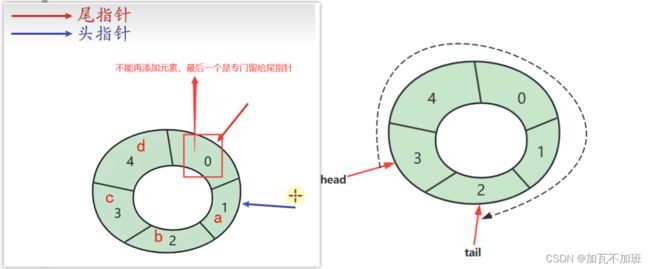
判断满
判断该数组是否满:(尾指针的索引+1)%数组长度==头指针的索引
满之后的策略可以根据业务需求决定
-
例如我们要实现的环形队列,满之后就拒绝入队
代码:
//仅用head,tail判断空满,head,tail即为索引值
public class ArrayQueue implements Queue, Iterable{
private int head = 0;
private int tail = 0;
private final E[] array;
private final int length;
//SuppressWarnings:抑制警告
@SuppressWarnings("all")
public ArrayQueue(int capacity) {
//你设定的容量+1:在你添加满容量时,需要有多出一个的位置给尾指针
length = capacity + 1;
array = (E[]) new Object[length];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
array[tail] = value;
//当加到数组最大索引位置时,应该让tail=数组初始索引位置0
tail = (tail + 1) % length;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = array[head];
//当加到数组最大索引位置时,应该让tail=数组初始索引位置0
head = (head + 1) % length;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return array[head];
}
@Override
public boolean isEmpty() {
return tail == head;
}
@Override
public boolean isFull() {
return (tail + 1) % length == head;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E value = array[p];
p = (p + 1) % array.length;
return value;
}
};
}
} 判断空、满方法2
//修改在数组满的时候,不用给尾指针留个位置
引入 size
public class ArrayQueue2 implements Queue, Iterable {
private int head = 0;
private int tail = 0;
private final E[] array;
private final int capacity;
private int size = 0;
@SuppressWarnings("all")
public ArrayQueue2(int capacity) {
this.capacity = capacity;
array = (E[]) new Object[capacity];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
array[tail] = value;
tail = (tail + 1) % capacity;
size++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = array[head];
head = (head + 1) % capacity;
size--;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return array[head];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == capacity;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E value = array[p];
p = (p + 1) % capacity;
return value;
}
};
}
} 判断空、满方法3
-
head 和 tail 不断递增,用到索引时,再用它们进行计算,两个问题
-
如何保证 head 和 tail 自增超过正整数最大值的正确性
-
如何让取模运算性能更高
-
-
答案:让 capacity 为 2 的幂
public class ArrayQueue3 implements Queue, Iterable {
private int head = 0;
private int tail = 0;
private final E[] array;
private final int capacity;
@SuppressWarnings("all")
public ArrayQueue3(int capacity) {
if ((capacity & capacity - 1) != 0) {
throw new IllegalArgumentException("capacity 必须为 2 的幂");
}
this.capacity = capacity;
array = (E[]) new Object[this.capacity];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
array[tail & capacity - 1] = value;
tail++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = array[head & capacity - 1];
head++;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return array[head & capacity - 1];
}
@Override
public boolean isEmpty() {
return tail - head == 0;
}
@Override
public boolean isFull() {
return tail - head == capacity;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E value = array[p & capacity - 1];
p++;
return value;
}
};
}
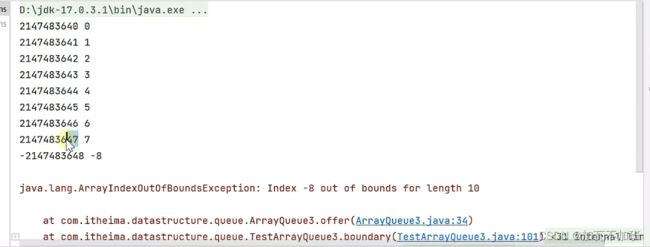
} 第三个方法暴露了一个问题:因为我们的head、tail都是整型int类型,正整数的最大值int:2147483647
测试:
如果是使用C语言就会解决:unsigned int 0 ~2^32-1
对于JAVA语言,它有种方法:可以将int整型超出的时候,及时将int转换为Long类型:
Integer.toUnsignedLong(tail)优化以后的代码:
/**
* @BelongsProject: arithmetic
* @BelongsPackage: com.hzp.algorithm.queue
* @Author: ASUS
* @CreateTime: 2023-09-25 11:26
* @Description: TODO 环形数组实现3.0
* @Version: 1.0
*/
//修改在数组满的时候,不用给尾指针留个位置
public class ArrayQueue3 implements Queue, Iterable{
private int head = 0;
private int tail = 0;
private E[] array;
//SuppressWarnings:抑制警告
@SuppressWarnings("all")
public ArrayQueue3(int capacity) {
array = (E[]) new Object[ capacity ];//这个时候就不需要给尾指针留个位置
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
//进行(int):数组中只能存储Int类型,不能是long类型所以要转换
array[(int) (Integer.toUnsignedLong(tail)% array.length)] = value;
tail++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = array[(int) (Integer.toUnsignedLong(head)% array.length)];
head++;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return array[(int) (Integer.toUnsignedLong(head)% array.length)];
}
@Override
public boolean isEmpty() {
return head==tail;
}
@Override
public boolean isFull() {
return tail-head==array.length;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p!=tail;
}
@Override
public E next() {
E value = array[(int) (Integer.toUnsignedLong(p)%array.length)];
p++;
return value;
}
};
}
} 判断空、满方法4
我们以二进制的角度来看求模运算的规律:
//求模运算:
// 被除数是什么都无所谓
// 如果除数是2的n次方
// 那么被除数的后n位即为余数(馍)
// 求被除数的后n位方法:与2^n-1按位与
演示:
总结规律:当除数是2的n次方,则余数是被除数的二进制后n位,被除数剩余的二进制就是商的二进制
对于我们求模运算而言,我们只需要余数即可:
所以结论:求余数:被除数与2^n-1按位与即可得到余数:
//求模运算:
// 如果除数是2的n次方
// 那么被除数的后n位即为余数(馍)
// 求被除数的后n位方法:与2^n-1按位与
public class ArrayQueue3_1 implements Queue, Iterable{
private int head = 0;
private int tail = 0;
private E[] array;
//SuppressWarnings:抑制警告
@SuppressWarnings("all")
//这个方法的条件就是 capacity的取值必须是2的n次方
public ArrayQueue3_1(int capacity) {
array = (E[]) new Object[ capacity ];//这个时候就不需要给尾指针留个位置
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
//进行(int):数组中只能存储Int类型,不能是long类型所以要转换
//array[(int) (Integer.toUnsignedLong(tail)% array.length)] = value;
//以下方法比以上方法的优点:1.&的运算更加优化 2.这也防止了int类型超出最大值的情况
array[tail& (array.length-1)]=value;
tail++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
//E value = array[(int) (Integer.toUnsignedLong(head)% array.length)];
E value = array[head& (array.length-1)];
head++;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
//return array[(int) (Integer.toUnsignedLong(head)% array.length)];
return array[head& (array.length-1)];
}
@Override
public boolean isEmpty() {
return head==tail;
}
@Override
public boolean isFull() {
return tail-head==array.length;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p!=tail;
}
@Override
public E next() {
//E value = array[(int) (Integer.toUnsignedLong(p)%array.length)];
E value = array[p& (array.length-1)];
p++;
return value;
}
};
}
} 但是注意:这个方法的条件就是 capacity的取值必须是2的n次方!!!!
因此,这个方法是有缺陷的。
判断空、满方法5
这个方法的条件就是 capacity的取值没有限制
就是对于第四种方法的优化:
第一种优化:就是对于“当输入的数不是2的幂则跑异常”:
//1.抛异常:当输入的数不是2的幂则跑异常
if(((capacity&capacity-1)!=0)){
throw new IllegalArgumentException("capactiy 必须是2的幂");
}对于“capacity&capacity-1”演示:
第二种优化:将输入的数不是2的幂改成2^n
这是利用第一种结论来写:
/*
当我输入的是数是30
c=30;
2^4 == 16
2^4.? == 30
2^5 == 32
我们要找到的是这个数最近并且大于这个数的2^n:
对于幂的获取:log2(30)==4.? --->(int)log2(30)==4 -->(int)log2(30)+1 ==5
int c=30;
int n= (int)(Math.log10(c-1)/Math.log10(2))+1;
System.out.println(n);
System.out.println(1<利用第二种结论:求离c最近,比c大的2^n(方法2)
c=30;
c -= 1;
c |= c >> 1;
c |= c >> 2;
c |= c >> 4;
c |= c >> 8;
c |= c >> 16;
c += 1;代码:
public class ArrayQueue3_2 implements Queue, Iterable{
private int head = 0;
private int tail = 0;
private E[] array;
//SuppressWarnings:抑制警告
@SuppressWarnings("all")
public ArrayQueue3_2(int capacity) {
//1.抛异常:当输入的数不是2的幂则跑异常
if(((capacity&capacity-1)!=0)){
throw new IllegalArgumentException("capactiy 必须是2的幂");
}
//2.将输入的数不是2的幂改成2^n
capacity -= 1;
capacity |= capacity >> 1;
capacity |= capacity >> 2;
capacity |= capacity >> 4;
capacity |= capacity >> 8;
capacity |= capacity >> 16;
capacity += 1;
array = (E[]) new Object[ capacity ];//这个时候就不需要给尾指针留个位置
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
//进行(int):数组中只能存储Int类型,不能是long类型所以要转换
//array[(int) (Integer.toUnsignedLong(tail)% array.length)] = value;
//以下方法比以上方法的优点:1.&的运算更加优化 2.这也防止了int类型超出最大值的情况
array[tail& (array.length-1)]=value;
tail++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
//E value = array[(int) (Integer.toUnsignedLong(head)% array.length)];
E value = array[head& (array.length-1)];
head++;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
//return array[(int) (Integer.toUnsignedLong(head)% array.length)];
return array[head& (array.length-1)];
}
@Override
public boolean isEmpty() {
return head==tail;
}
@Override
public boolean isFull() {
return tail-head==array.length;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p!=tail;
}
@Override
public E next() {
//E value = array[(int) (Integer.toUnsignedLong(p)%array.length)];
E value = array[p& (array.length-1)];
p++;
return value;
}
};
}
}