哈希原理和解决哈希冲突方法
第一 哈希介绍
哈希和红黑树是我早期就听过的名词,却一直没见到真面目,实现哈希后才发现原来我早就使用过了哈希。看下面例题。
用map和set都可以轻松解决,但是在我写这题时我还不会用map和set,我用了另一种方法。看下面代码。先定义一个数组,因为题目说了astr中只会出现小写字母,所以数组只需要开26个空间,然后将字母的ASCii码值-'a'做下标,例如astr[i]是字符a,-'a'那下标就是0,就在arr[0]处++,表示出现次数+1, 如果arr在这个下标处存的数字不为0,那表示出现次数不为一,返回false,表示字符不唯一出现。代码如下,这种映射法存字符就是一种哈希函数,非常方便查找,我们用arr[astr[i]-'a']找出现次数的时间复杂度是O(1),如果用map和set则要O(logn)。这就是哈希强大之处。
class Solution {
public:
bool isUnique(string astr)
{
int arr[26]={0};
for(int i=0;i事实上哈希还和计数排序有点相似,
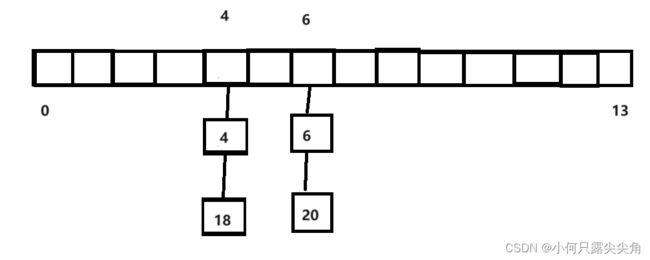
如果是这个数组是给哈希用的,当4来了的时候,它的放置下标i=key%14,(这就是另外一个常用的哈希函数,由于值和空间是多对一的,由此产生出哈希冲突等问题),所以下标i就是4,并且把4放到该数组中去,而计数排序是把出现次数放入数组,这就是两者的不同之处。
如果又来了个数字18,i计算结果也是4,那这时候难道让18去覆盖4吗,当然不行,这时候出现的状况就称为哈希冲突,是不是很好理解,那应该存哪呢?既然4位置处满了,那就往后找下一个空格处存就好了,这会不会找不到,丢了呢?不会,你想想,首先如果4下标位置处不在,那就肯定是存在4的后面,一直往后找就行了,当你遇到空格了都还没找到,那就说明这个数不存在,而如何找下一个空格则有不同的方法,如果是一个个往后找,这就是闭散列的线性探测,如果是key=key+i^2(i为查找次数),则称为二次探测,可以拉开数据间的空隙,不会让数据都堆积在一起,了解即可。下面来看看闭散列线性探测的相关实现。
第二 闭散列实现
1 HashData类
可以认为哈希数组中每个元素是个HashData类型的数据,这个自定义类型内存了个pair类型的 _kv,pair的first就是key,用来计算下标,算到什么值,就把pair放到哪个位置,而不是对pair的second++,不要和map搞混了,写博客才发觉HashData存个pair好像容易混淆。
enum State
{
Empty,
Exist,
Delete
};
template
struct HashData
{
pair _kv;
State _state = Empty; 默认为空
}; 还有个成员是_state,这个是什么呢?这就涉及到前面忽略的问题,如果原来4下标放了一个4,再来个18会冲突,往后存,如果之后我们把4删除了,然后找18,那先用18算key,从4开始找,可以4这个位置元素被删了,那一般也就是置为零,表示该元素空了,这不就是找到空格,算没找到18,直接结束吗。
诶,好像哪里不对,那你可能会说不对,用零表示被删,-1表示空,这样18来找的时候,发现4上是0,就知道这是被删除了,18可能在后面,这么来看好像说得通,可是用数字表示状态本身就有个大问题,你看看0下标处本来就要存0,难道这表示删除?然后14来了把它覆盖?
回想红黑树,是用枚举常量表示节点是红还是黑的状态,那我们也可以用枚举常量表示空,删除和存在三种状态,而且十分直观。
2 HashTable类
在看insert成员函数时,有个概念要提一下,负载因子,由于线性探测是往后找空位置放冲突元素,本质上是占用别人的位置来解决自己的冲突,但是如果哈希表上的空格越来越少,那每次插入元素都要往后查找可能接近O(N),就出现退化了,所以用_size记录存放的元素个数,当超过一定值,就要扩容,保持哈希表的空格是比较充裕的,这就会使得空间上会有浪费,这是无法避免的。
template>
class HashTable
{
public:
bool insert(const pair kv)
{
Hashfun hf;
if (_size * 10 / _table.size() >= 7) 负载因子大于0.7时,扩容
{
size_t newsize = _table.size() * 2;
HashTable newtable;
newtable._table.resize(newsize);先开好空间,避免频繁扩容
遍历旧表,将数据弄到新表
for(size_t i = 0; i < _table.size(); i++)
{
if(_table[i]._state==Exist)//该数据存在才插入
newtable.insert(_table[i]._kv);
}
新旧表交换,只用交换_table, _size无需变换
_table.swap(newtable._table);
原先的哈希表无需写析构函数,是vector会调用自己析构,vector存的元素是HashData
HashData内存的是一个pair,所以都无资源需要我们释放。
}
仿函数处理key,下面讲模板参数会提及
int hashi = hf(kv.first) % (_table.size());
线性探测
while (_table[hashi]._state == Exist) 该位置已存在数字
{
if (_table[hashi]._state == Exist && _table[hashi]._kv == kv)
return false; 已存在该值
hashi++;
hashi %= _table.size(); 防止越界
}
_table[hashi]._kv = kv;
_table[hashi]._state = Exist;
_size++;
return true;
}
private:
vector > _table;
size_t _size = 0; 记录哈希表中存在元素个数
}; 3 模板参数解析
先前已经把哈希的基本原理解释完了,但是有个细节点要先补充一下,然后才好把剩下的成员函数介绍完。我们说来了一个4,或者18,就是直接%数组空间大小求下标,如果哈希表要存一个字符串呢,怎么取模?首字符的ASCII码值?这样首字符相同的就都会冲突了,那就把字符串全部的ASCII码值加起来,诶这个貌似极大地减少了冲突,那如果我拿出下面这两个例子呢?"abc"和"bbb"这个也会冲突,阁下又该如何应对呢?前辈们早已经研究出了算法,也就是BKDR算法,本文用仿函数实现的,如下。
先说个我们写的仿函数巧妙的地方,我们用了模板参数,如果K是int,double这些内置类型,那就调用下面的直接返回,如果是string,那就调用更匹配,就不用我们显示传了,它会直接根据DefaultHashfunc
template
struct DefaultHashfunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
struct DefaultHashfunc 模板特化
{
改进,加上所有字符的ASCii码值,并且用BKDR算法降低冲突
size_t operator()(const string& s)
{
int hash = 1;
for (auto e : s)
{
hash = hash * 131 + e;
BKDR,实质是在加上字符的ASCII码时加一个数越来越大的数字
hash*= 131;
}
return (size_t)hash;
最后把求的值之和返回,用于%数组空间大小,
溢出也无所谓,因为find求下标前也会溢出,也就会用截断后的去找
}
};
4 其余成员函数
HashTable() 构造函数
{
_table.resize(5); 开空间得用resize,reserve会越界,例如reserse 4个空间,
我们却不能直接访问这几个空间,因为vector内有效元素为0,[]访问第一个后面的空间
会报错
}
bool Erase(const K&key)
{
pair ret = find(key); 先找到该节点
if (ret)
{
ret.second = Delete; 修改状态
return true;
}
return false;
}
HashData* find(const K&key)
{
Hashfun hf;
int hashi = hf(key) % (_table.size()); 算下标
while(_table[hashi]._state!=Empty) 该位置不为空,就继续往后找
{
if (_table[hashi]._state == Exist&&_table[hashi]._kv.first==key)
{
return (HashData*)&_table[hashi];//防止该编译器不支持隐式类型转换
}
hashi++;
}
//找到空位置,说明没有该元素,返回空
return nullptr;
} 这就是哈希闭散列的全部实现,虽然比红黑树简单,但是细节点也不少。如果看到这里的读者还有冲劲,就向着开散列冲刺吧,我第一次接触感觉挺震撼的。
第三 开散列实现
闭散列解决冲突的方法终究还是太粗暴了,冲突就占用其它元素的位置,把火都烧到别的地方了,所以大佬们又想到一种方法,哈希桶。我画个来演示大家就知道了。
这种方式的巧妙在于将冲突元素化为链表链接,形成一个桶,故称哈希桶,不管有多少冲突,都插入到链表中去,查找就在链表里找,找到空都没找到那就说明该元素不存在。接下来看实现
1 HashNode类
先前的HashData类之所以没有写构造函数,那是数组开好空间了,初始化好了,我们只要往里面放数据就好了,现在是insert的时候要new一个节点出来,我们写好构造函数,方便new初始化,也可以后面自己在手动赋值,反正节点指针你也有,修改节点内的数据还不是简简单单吗。
template
struct HashNode
{
HashNode(const pair& kv)
:_kv(kv)
,_next(nullptr)
{
;
}
pair _kv;
HashNode* _next;
}; 2 HashBucketTable类
有了前面开散列的基础,接下来的介绍就可以省略一点了。
1 先看构造和析构函数以及成员变量
template>
class HashBucketTable
{
public:
typedef HashNode Node;
HashBucketTable()
{
_table.resize(5); 直接resize开空间就好,注意别用reserve
}
~HashBucketTable()
{
for (size_t i = 0; i < _table.size(); i++) 遍历哈希表上的链表
{
Node* cur = _table[i];
while (cur) 一个一个delete
{
Node* next = cur->_next;
_table[i] = next;
delete cur;
cur = next;
}
}
}
private:
vector _table; 存的是一个节点的指针,节点通过_next指针变量链接其它节点
size_t _size=0;
}; 2 其余成员函数
bool insert(const pair& kv)
{
//查找该节点是否已经存在
if(find(kv.first))
return false;
Hashfun hf; 将自定义类型key转为整数的仿函数
if (_size >= _table.size()) 当节点数足够哈希表的每个桶上挂上一个节点就扩容
{
开新表
size_t newsize = _table.size() * 2;
vector newtable;
newtable.resize(newsize);
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
注意链接后面的节点,免得丢了
Node* next = cur->_next;
_table[i] = next;
size_t hashi = hf(cur->_kv.first) % newtable.size();
要重新计算映射下标,size变了,取模结果可能会变
将原先节点搬到新表
cur->_next = newtable[hashi];
newtable[hashi] = cur;
cur = next; 搬下个节点
}
}
_table.swap(newtable);
}
正常插入数据
size_t hasi = hf(kv.first) % _table.size();
Node* newnode = new Node(kv);
newnode->_next = _table[hasi];
_table[hasi]=newnode;
_size++;
return true;
}
HashBucketTable(HashBucketTable& ht)
{
Hashfun hf;
_table.resize(ht._table.size());
for (size_t i = 0; i < ht._table.size(); i++) 遍历哈希表ht
{
Node* cur = ht._table[i];
while (cur) 遍历该桶
{
Node* newnode = new Node(cur->_kv);
size_t hashi = hf(cur->_kv.first)% _table.size();
newnode->_next = _table[hashi];
_table[hashi] = newnode;
cur = cur->_next;//去桶的下一个节点
}
}
}
Node* find(const K& key)
{
Hashfun hf;
size_t hashi = hf(key) % _table.size();
Node* cur = _table[hashi]; 直接定位到该桶去找
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
bool Erase(const K& key)
{
Hashfun hf;
if(!find(const K& key))先用key找节点,找不到返回false
return false;
size_t hashi = hf(key) % _table.size();
Node* pre = nullptr;
Node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
{
if (pre == nullptr) 处理头删
{
_table[hashi] = cur->_next; 链接
}
else
{
pre->_next= cur->_next;
}
delete cur;
--_size; 负载因子要--
return true;
}
pre = cur;
cur = cur->_next; 往链表后找删除节点
}
return false;
} 哈希桶查找数据几乎可以说完美了,只是理论上还会有个缺陷,那就是链表可能还是太长,那怎么办呢?有人就设计将其化为一颗红黑树,红黑树加哈希桶,这就几乎万无一失了,链表转红黑树也就是遍历链表把数据一个个插入到红黑树即可。