网易云音乐推荐算法

网易云音乐的歌单推荐算法是怎样的？

 

这就是amazon发明的“喜欢这个商品的人，也喜欢某某”算法。
其核心是数学中的“多维空间中两个向量夹角的余弦公式”，当初我的确是被这算法惊艳到了。

=============2014-12-01 更新 =============================
不好意思，之前说的有误，特来更正兼补充。

“商品推荐”系统的算法( Collaborative filtering )分两大类，
第一类，以人为本，先找到与你相似的人，然后看看他们买了什么你没有买的东西。这类算法最经典的实现就是“多维空间中两个向量夹角的余弦公式”；
第二类, 以物为本直接建立各商品之间的相似度关系矩阵。这类算法中最经典是'斜率=1' (Slope One)。amazon发明了暴力简化的第二类算法，‘买了

这个商品的人，也买了xxx’。

我们先来看看第一类，最大的问题如何判断并量化两人的相似性，思路是这样 -- 
例子：
有3首歌放在那里，《最炫民族风》，《晴天》，《Hero》。
A君，收藏了《最炫民族风》，而遇到《晴天》，《Hero》则总是跳过；
B君，经常单曲循环《最炫民族风》，《晴天》会播放完，《Hero》则拉黑了
C君，拉黑了《最炫民族风》，而《晴天》《Hero》都收藏了。

我们都看出来了，A,B二位品味接近，C和他们很不一样。
那么问题来了，说A，B相似，到底有多相似，如何量化？

我们把三首歌想象成三维空间的三个维度，《最炫民族风》是x轴，《晴天》是y轴，《Hero》是z轴，对每首歌的喜欢程度即该维度上的坐标，
并且对喜欢程度做量化(比如： 单曲循环=5, 分享=4, 收藏=3, 主动播放=2 , 听完=1, 跳过=-1 , 拉黑=-5 )。
那么每个人的总体口味就是一个向量，A君是 (3,-1,-1)，B君是(5,1,-5)，C君是(-5,3,3)。 (抱歉我不会画立体图)
我们可以用向量夹角的余弦值来表示两个向量的相似程度， 0度角(表示两人完全一致)的余弦是1， 180%角(表示两人截然相反)的余弦是-1。

根据余弦公式, 夹角余弦 = 向量点积/ (向量长度的叉积) = ( x1x2 + y1y2 + z1z2) / ( 跟号(x1平方+y1平方+z1平方 ) x 跟号(x2平方+y2平方+z2平方 ) )
可见 A君B君夹角的余弦是0.81 ， A君C君夹角的余弦是 -0.97 ，公式诚不欺我也。
以上是三维(三首歌)的情况，如法炮制N维N首歌的情况都是一样的。
假设我们选取一百首种子歌曲，算出了各君之间的相似值，那么当我们发现A君还喜欢听的《小苹果》B君居然没听过，相信大家都知道该怎么和B君推荐了吧。

第一类以人为本推荐算法的好处我想已经很清楚了，那就是精准！
代价是运算量很大，而且对于新来的人(听得少，动作少)，也不太好使，
所以人们又发明了第二类算法。

假设我们对新来的D君，只知道她喜欢最炫民族风，那么问题来了，给她推荐啥好咯？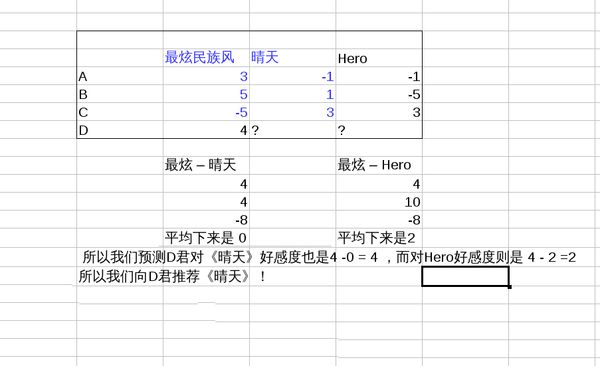

如图，推荐《晴天》！

呵呵，第二类算法的好处大家也看出来了，简单粗暴好操作(也适合map-reduce)，可精度差了点。

所以，各家网站真正的推荐算法，是他们在综合上述两类算法的基础上，各自研制并且不断地改进调节的，外人不得而知！ ^_^

=== 2014-12-03 再补充 ===

多谢 @刘彦彬 给了一个非常专业的评论 ，不贴出来可惜了。
“这个只能说是理论基础。歌曲不考虑热门冷门，同时不考虑用户数和歌曲数计算复杂度的话第一一天内离线数据计算不完的（当然网易云音乐用户量

小全量暴力计算当我没说），实际应用起来复杂很多了。现在的推荐系统并不存在一种算法通吃，除了算法上的问题，还需要考虑基础数据的影响因素，

比如两张歌单有多少歌曲重合，歌单的质量是怎么样的。” 

我上一帖也说了，
'向量夹角余弦' 解决的是‘量化顾客口味相似度’的问题(是最经典的解法，也有别的解法)，
不是有了它就能轻易实现第一类算法的，难处在后面咯。
我不是干‘CF/算法/数据挖掘/互联网’的，只是几年前偶尔瞄到过这方面文章被惊艳了一下，
见到这题就随口抖了个机灵，然后被评论区几位带板凳来的朋友给推上来了 ^_^

既然大家都这么有兴趣，我在来抛块砖，说说‘有了理论基础之后咋整’的思(nao3)考(dong4)。
继续第一类算法的话题，目标“每日歌曲推荐”(其实题主感兴趣的是这个吧，旁边‘根据你喜欢的xxx推荐的yyy歌单’我觉得不咋样)。
首先就是如何定维度。 
直接用‘歌’当维度是不行的，第一是太多了算不过来，第二维度数一直猛涨也不是个事。
用‘歌单’或者‘专辑’，‘演唱/演奏者’呢？也有类似的困难。
说到这里大家应该都意识到了，咱不是还有‘tag’嘛！
云音乐初期，tag是可以由大家自己填的，我记得我填过‘莫扎特’，‘钢协’，‘交响’这样的tag，现在都不见了吧。
一段时间之后，tag无法自填了，只能从云音乐给的tag lib中选，这肯定有原因的。
我的推测就是，他们需要用tag来当作维度，所以不希望tag数经常变化。
第一阶段，他们需要搜集用户的输入来做出tag lib，
第二阶段，他们构建了多维度空间，就不希望再动维度了，因此关闭了自填tag的功能。

假设就用tag做为维度，那么第二个难处在于，维度上的'刻度'必须有正有负才好使，
用户没有机会直接表达对tag的好恶(不能收藏，播放，跳过一个tag)，如何定刻度呢。
我认为每一首歌背后是有其所属tags这个属性的，这个属性在UI上看不到很可能是因为比较容易引起口水。
歌往往隶属于很多歌单，而那些歌单都是有tags的，根据那些歌单的播放数收藏数分享数可以决定其'权威性'，
取'权威性'高的歌单的tag，就可以得到每首歌的tag属性。
然后用户在表达对一首首歌的好恶的时候，其实就不知不觉地影响了他在相应维度上的刻度。

假设维度和刻度都这样解决，那么我们可以对每个用户做出‘口味向量’了，接下来的难处是，
啥时候算/如何保存‘用户相似性’？
所有用户两两算一下相似性，存为一个NxN的矩阵，这种事情不是闹这玩的。

其实到了这一步，不考虑‘以人为本’，直接根据我喜欢的tag，从各tag里挑一些人气高的，或者蹿升快的歌来推荐也算是能交差了。
不过那样的话，就容易同质化，也就不易让用户‘惊艳’了。
让我们继续沿着第一类算法的思路琢磨琢磨。

多维度空间还有一大好处是，有‘像限’这种的概念，
比如我们可以粗暴地假设，和我同一个像限的人，就是和我‘相似’的人，
如果因为维度太多，或者初期用户太少等原因找不到同像限的人， 还可以去‘相邻’的像限找嘛。
OK，假设我们根据tag以及自己的像限，找到了一批和自己‘气味相投’的人。
再丛这批人中，选几个‘和我夹角余弦’最大(再综合一下个人名声比如星标，粉丝数，和我的互动度等，更好)的人，
从他们听过而我没听过的歌中，再选一批 他们喜欢，或者他们新听到，新收藏，或者总人气高的等等，
就可以说是“根据我的口味生成”的“每日歌曲推荐”了。

 

 

这里我想给大家介绍另外一种推荐系统，这种算法叫做潜在因子（Latent Factor）算法。这种算法是在NetFlix（没错，就是用大数据捧火

《纸牌屋》的那家公司）的推荐算法竞赛中获奖的算法，最早被应用于电影推荐中。这种算法在实际应用中比现在排名第一的 @邰原朗 所

介绍的算法误差（RMSE）会小不少，效率更高。我下面仅利用基础的矩阵知识来介绍下这种算法。

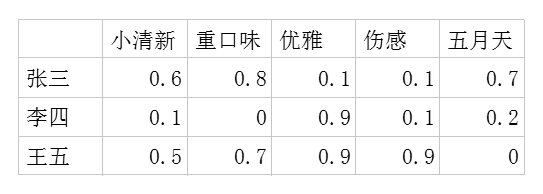
这种算法的思想是这样：每个用户（user）都有自己的偏好，比如A喜欢带有小清新的、吉他伴奏的、王菲等元素（latent factor），

如果一首歌（item）带有这些元素，那么就将这首歌推荐给该用户，也就是用元素去连接用户和音乐。每个人对不同的元素偏好不同，而

每首歌包含的元素也不一样。我们希望能找到这样两个矩阵：

一，用户-潜在因子矩阵Q，表示不同的用户对于不用元素的偏好程度，1代表很喜欢，0代表不喜欢。比如下面这样：

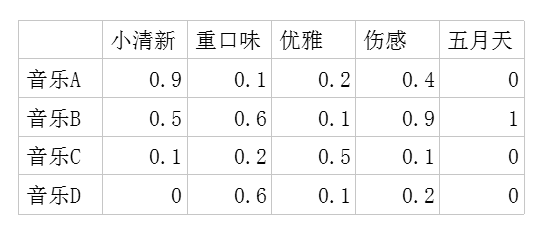
二，潜在因子-音乐矩阵P，表示每种音乐含有各种元素的成分，比如下表中，音乐A是一个偏小清新的音乐，含有小清新这个Latent Factor

的成分是0.9，重口味的成分是0.1，优雅的成分是0.2……

利用这两个矩阵，我们能得出张三对音乐A的喜欢程度是：张三对小清新的偏好*音乐A含有小清新的成分+对重口味的偏好*音乐A含有

重口味的成分+对优雅的偏好*音乐A含有优雅的成分+……

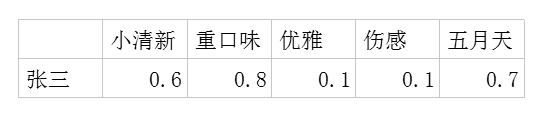
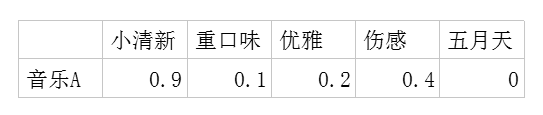
即：0.6*0.9+0.8*0.1+0.1*0.2+0.1*0.4+0.7*0=0.69

每个用户对每首歌都这样计算可以得到不同用户对不同歌曲的评分矩阵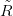。（注，这里的破浪线表示的是估计的评分，接下来我们还会

用到不带波浪线的R表示实际的评分）：

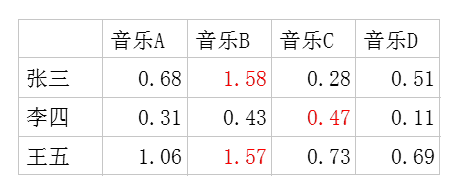
因此我们队张三推荐四首歌中得分最高的B，对李四推荐得分最高的C，王五推荐B。

如果用矩阵表示即为：

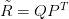
下面问题来了，这个潜在因子（latent factor）是怎么得到的呢？

由于面对海量的让用户自己给音乐分类并告诉我们自己的偏好系数显然是不现实的，事实上我们能获得的数据只有用户行为数据。

我们沿用 @邰原朗的量化标准：单曲循环=5, 分享=4, 收藏=3, 主动播放=2 , 听完=1, 跳过=-2 , 拉黑=-5，在分析时能获得的

实际评分矩阵R，也就是输入矩阵大概是这个样子：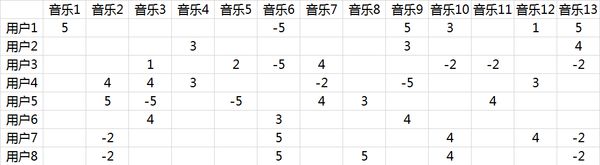

事实上这是个非常非常稀疏的矩阵，因为大部分用户只听过全部音乐中很少一部分。如何利用这个矩阵去找潜在因子呢？这里主要应用到的

是矩阵的UV分解。也就是将上面的评分矩阵分解为两个低维度的矩阵，用Q和P两个矩阵的乘积去估计实际的评分矩阵，而且我们希望估计的评分矩阵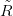

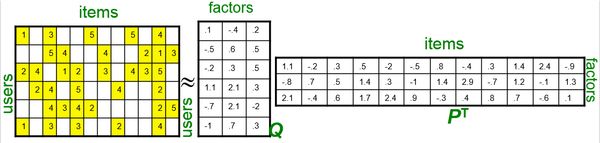
和实际的评分矩阵不要相差太多，也就是求解下面的目标函数：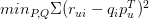

这里涉及到最优化理论，在实际应用中，往往还要在后面加上2范数的罚项，然后利用梯度下降法就可以求得这P,Q两个矩阵的估计值。这里我们

就不展开说了。例如我们上面给出的那个例子可以分解成为这样两个矩阵：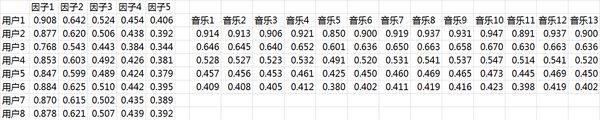

这两个矩阵相乘就可以得到估计的得分矩阵：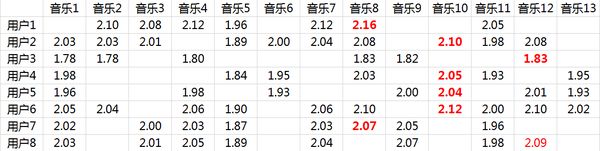

将用户已经听过的音乐剔除后，选择分数最高音乐的推荐给用户即可（红体字）。

在这个例子里面用户7和用户8有强的相似性：

从推荐的结果来看，正好推荐的是对方评分较高的音乐：