深度学习笔记7：模型选择+过拟合和欠拟合
模型选择
例子：预测谁会偿还贷款
- 银行雇你来调查谁会偿还贷款
- 你得到了100个申请人的信息
- 其中五个人在3年内违约了
发现：
- 5个人在面试的时候都穿
- 模型也发现了这个强信号
- 这会有什么问题？
训练误差和泛化误差
- 训练误差：模型在训练数据上的误差
- 泛化误差：模型在新数据上的误差（主要关注）
- 例子：根据模考成绩来预测未来考试分数
- 在过去的考试中表现很好（训练误差）不代表未来考试一定会好（泛化误差）
- 学生A通过背书在模考中拿到好成绩
- 学生B知道答案后面的原因
验证数据集和测试数据集
- 验证数据集：一个用来评估模型好坏的数据集。用来调整超参数
- 例如拿出50%的训练数据
- 不要跟训练数据混在一起（常犯错误）
- 测试数据集：只用一次的数据集。是一个新的数据集，不能用来调整超参数
- 例如未来考试
- 出价的房子的实际成交价
- 用在Kaggle私有排行榜中的数据集
K-折交叉验证
- 在没有足够多数据时使用（这是常态）
- 算法：
- 将训练数据分割成K块
- For i = 1，…，K
- 使用第 i 块作为验证数据集，其余的做为训练数据集
- 报告K个验证集误差的平均
- 常用：
K=5或10
总结
- 训练数据集：训练模型参数
- 验证数据集：选择模型超参数
- 非大数据集上通常使用K-折交叉验证
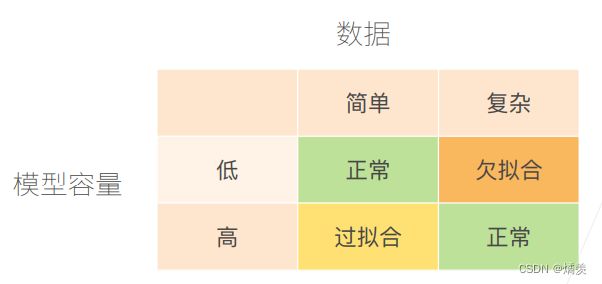
过拟合和欠拟合
模型容量：模型的复杂度，（低：简单模型，高：复杂模型）
根据数据的简单和复杂来选择模型容量
模型容量
-
拟合各种函数的能力
-
低容量的模型难以拟合训练数据
-
高容量的模型可以记住所有的训练数据
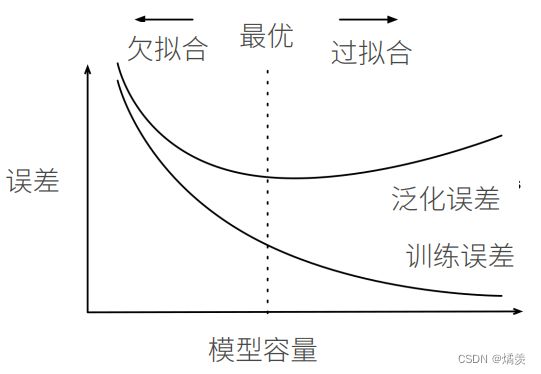
模型容量的影响
当模型容量较为低时，训练误差比较高，随着模型容量的增加，训练误差开始下降；泛化误差会降到某个点时候会上升，在欠拟合和过拟合中会有一个最优点。
深度学习核心：模型足够大，通过各种手段去控制模型容量，使得泛化误差下降
估计模型容量
-
难以在不同的种类算法之间比较
- 例如树模型的神经网络
-
给定一个模型种类，将有两个主要因素
-
参数的个数
-
参数值的选择范围
若参数选择范围大，则模型复杂度比较高，若小，则模型容量低
左：线性模型，数据数：d，参数个数：d+1
右：单隐藏层感知机，隐藏层：m，分类类别数：k，参数个数：(d+1)m+(m+1)k
根据参数个数来简单判断模型容量的高低，右>左
-
VC维
- 统计学习理论的一个核心思想
- 对于一个分类模型，VC等于一个最大的数据集的大小，不管如何给定标号，都存在一个模型来对它进行完美分类
线性分类器的VC维
-
2维输入的感知机，VC维=3
-
能够分类任何三个点，但不是4个（XOR）
-
-
支持N维输入的感知机的VC维是N+1
-
一些多层感知机的VC维O(Nlog2N)
VC维的用处
- 提供为什么一个模型好的理论依据
- 它可以衡量训练误差和泛化误差之间的间隔
- 但深度学习中很少使用
- 衡量不是很准确
- 计算深度学习模型的VC维很困难
数据复杂度
多个重要因素
- 样本个数
- 每个样本的元素个数
- 时间、空间结构
- 多样性
总结
- 模型容量需要匹配数据复杂度，否则可能导致欠拟合和过拟合
- 统计机器学习提供数学工具来衡量模型复杂度
- 实际中一般靠观察训练误差和验证误差
代码实现
模型选择、欠拟合和过拟合
通过多项式拟合来交互地探索这些概念
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
使用以下三阶多项式来生成训练和测试数据的标签：
y = 5 + 1.2 x − 3.4 x 2 / 2 ! + 5.6 x 3 / 3 ! + ϵ w h e r e ϵ ∼ N ( 0 , 0. 1 2 ) y=5+1.2x−3.4x^{2}/2!+5.6x^{3}/3!+ϵ where ϵ∼N(0,0.1^{2}) y=5+1.2x−3.4x2/2!+5.6x3/3!+ϵwhereϵ∼N(0,0.12)
max_degree = 20
n_train, n_test = 100, 100 #100个训练样本 100个测试样本（验证样本）
true_w = np.zeros(max_degree)
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)
看一下前2个样本
true_w, features, poly_features, labels = [
torch.tensor(x, dtype=torch.float32)
for x in [true_w, features, poly_features, labels]]
features[:2], poly_features[:2, :], labels[:2]
结果：
实现一个函数来评估模型在给定数据集上的损失
def evaluate_loss(net, data_iter, loss):
"""评估给定数据集上模型的损失。"""
metric = d2l.Accumulator(2)
for X, y in data_iter:
out = net(X) #输出
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
定义训练函数
def train(train_features, test_features, train_labels, test_labels,
num_epochs=400):
loss = nn.MSELoss()
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False)) #定义单层的线性回归网络
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),
batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),
batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
xlim=[1, num_epochs], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(
net, train_iter, loss), evaluate_loss(net, test_iter, loss)))
print('weight:', net[0].weight.data.numpy())
三阶多项式函数拟合(正态)
train(poly_features[:n_train, :4], poly_features[n_train:, :4], #数据和模型相匹配
labels[:n_train], labels[n_train:])
结果：weight: [[ 5.005174 1.2039171 -3.392575 5.5782466]]
线性函数拟合(欠拟合)
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
labels[:n_train], labels[n_train:])
结果：weight: [[3.5490751 3.4069588]]
高阶多项式函数拟合(过拟合)
train(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:], num_epochs=1500)
结果：
weight: [[ 4.9742413 1.2692064 -3.239483 5.2089176 -0.4539587 1.2671229
-0.1390583 0.27213308 -0.10114118 0.10512644 -0.0553343 -0.19972092
0.16716152 0.20946853 0.13661966 0.22037429 -0.22302164 -0.16093664
0.16818342 -0.14300445]]
