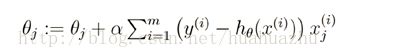机器学习——梯度下降法

梯度下降（Gradient Descent）算法是机器学习中使用非常广泛的优化算法。当前流行的机器学习库或者深度学习库都会包括梯度下降算法的不同变种实现。

接下来我将介绍三种梯度下降算法：随机梯度下降算法、批量梯度下降算法、小批量梯度下降算法

• 梯度下降

梯度下降原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快，很明显从起始点出发最陡的地方下降最快，这就是我们的负梯度方向（此处讨论求最小值解，若求最大值则用正梯度方向）。

这是线性回归中的损失函数，类似于最小二乘法进行拟合，这也是迭代评判的标准。

梯度下降法的关键是搜索方向和步长，步长太大容易导致振荡，步长太小迭代时间太长，搜索方向要寻找速度最快的方向。

使用梯度下降算法的步骤：

1）对θ赋初始值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得目标损失函数J(θ)按梯度下降的方向进行减少。

3）当下降的高度小于某个定义的值，则停止下降，否则继续迭代，直至到达循环最大次数。

这是梯度方向的推导过程：

收敛条件：

随机梯度下降算法（Stochastic Gradient Descent）

我们将训练集进行逐个计算损失函数，并更新权值θ，一直循环执行完所有训练集，然后进行误差比较，看是否逼近真实值，若逼近算法终止，否则继续进行

优点：单次处理速度快，迭代量较小

缺点：总体迭代次数过多，不易于并行实现，且噪声影响大，搜索方向变动频繁

#coding=utf_8
""""
随机梯度下降法
公式：theta ：= theta + alpha*sigma((y-h)*x)
"""
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 构造训练数据
x = np.arange(0., 10., 0.2)
m = len(x)  # 训练数据点数目
print(m)
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 将偏置b作为权向量的第一个分量
target_data = 2 * x + 5 + np.random.randn(m)

# 两种终止条件
loop_max = 10000  # 最大迭代次数(防止死循环)
epsilon = 1e-3

# 初始化权值
np.random.seed(0)  #制造一个随机数种子
theta = np.random.randn(2)  #产生两个随机theta值，作为初值

alpha = 0.001  # 步长(注意取值过大会导致振荡即不收敛,过小收敛速度变慢)
diff = 0.
error = np.zeros(2)
count = 0  # 循环次数
finish = 0  # 终止标志

while count < loop_max:
    count += 1

    # 标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的
    # 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算
    for i in range(m):
        dif = (np.dot(theta, input_data[i]) - target_data[i]) * input_data[i]
        theta = theta - alpha * dif  # 注意步长alpha的取值,过大会导致振荡
    # theta = theta - 0.005 * sum_m      # alpha取0.005时产生振荡,需要将alpha调小

    # 判断是否已收敛
    if np.linalg.norm(theta - error) < epsilon:
        finish = 1
        break
    else:
        error = theta
    print('loop count = %d' % count, '\tw:', theta)
print('loop count = %d' % count, '\tw:', theta)

# check with scipy linear regression
#一种最小二成拟合的算法，具体可查阅https://baijiahao.baidu.com/s?id=1589000357170305884&wfr=spider&for=pc
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print('intercept = %s slope = %s' % (intercept, slope))

plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()

批量梯度下降算法（Batch Gradient Descent）

一次训练所有数据，然后进行迭代

优点：受噪声影响较小，易于找到全局最优解，总体迭代次数较少，易于并行处理

缺点：当数据量较大时，处理速度慢，步长过大时容易造成振荡

#coding=utf_8
""""
批量梯度下降法
公式：theta ：= theta + alpha*sigma((y-h)*x)
"""
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 构造训练数据
x = np.arange(0., 10., 0.2)
m = len(x)  # 训练数据点数目
print(m)
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 将偏置b作为权向量的第一个分量
target_data = 2 * x + 5 + np.random.randn(m)

# 两种终止条件
loop_max = 10000  # 最大迭代次数(防止死循环)
epsilon = 1e-3

# 初始化权值
np.random.seed(0)  #制造一个随机数种子
theta = np.random.randn(2)  #产生两个随机theta值，作为初值

alpha = 0.001  # 步长(注意取值过大会导致振荡即不收敛,过小收敛速度变慢)
diff = 0.
error = np.zeros(2)
count = 0  # 循环次数
finish = 0  # 终止标志

while count < loop_max:
    count += 1

    # 标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的
    # 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算
    sum_m = np.zeros(2)
    for i in range(m):
        dif = (np.dot(theta, input_data[i]) - target_data[i]) * input_data[i]
        sum_m = sum_m + dif
    # 当alpha取值过大时,sum_m会在迭代过程中会溢出
    theta = theta - alpha * sum_m  # 注意步长alpha的取值,过大会导致振荡
    # theta = theta - 0.005 * sum_m      # alpha取0.005时产生振荡,需要将alpha调小

    # 判断是否已收敛
    if np.linalg.norm(theta - error) < epsilon:
        finish = 1
        break
    else:
        error = theta
    print('loop count = %d' % count, '\tw:', theta)
print('loop count = %d' % count, '\tw:', theta)

# check with scipy linear regression
#一种最小二成拟合的算法，具体可查阅https://baijiahao.baidu.com/s?id=1589000357170305884&wfr=spider&for=pc
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print('intercept = %s slope = %s' % (intercept, slope))

plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()

小批量梯度下降算法（Mini_Batch Gradient Descent）

选择合适的批量数据进行处理，分多次进行，从而获得最优解，融合了以上两者优点，是个不错的选择。

#coding=utf_8
""""
小批量梯度下降法
公式：theta ：= theta + alpha*sigma((y-h)*x)
"""
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 构造训练数据
x = np.arange(0., 10., 0.2)
m = len(x)  # 训练数据点数目
print(m)
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 将偏置b作为权向量的第一个分量
target_data = 2 * x + 5 + np.random.randn(m)

# 两种终止条件
loop_max = 10000  # 最大迭代次数(防止死循环)
epsilon = 1e-3

# 初始化权值
np.random.seed(0)  #制造一个随机数种子
theta = np.random.randn(2)  #产生两个随机theta值，作为初值

alpha = 0.001  # 步长(注意取值过大会导致振荡即不收敛,过小收敛速度变慢)
diff = 0.
error = np.zeros(2)
count = 0  # 循环次数
finish = 0  # 终止标志
Minibatch=5 #小批量步长
while count < loop_max:
    count += 1

    # 标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的
    # 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算
    for k in range(0,m,Minibatch):
        sum_m = np.zeros(2)
        for i in range(Minibatch):
            dif = (np.dot(theta, input_data[i+k]) - target_data[i+k]) * input_data[i+k]
            sum_m = sum_m + dif
        # 当alpha取值过大时,sum_m会在迭代过程中会溢出
        theta = theta - alpha * sum_m  # 注意步长alpha的取值,过大会导致振荡

    # 判断是否已收敛
    if np.linalg.norm(theta - error) < epsilon:
        finish = 1
        break
    else:
        error = theta
    print('loop count = %d' % count, '\tw:', theta)
print('loop count = %d' % count, '\tw:', theta)

# check with scipy linear regression
#一种最小二成拟合的算法，具体可查阅https://baijiahao.baidu.com/s?id=1589000357170305884&wfr=spider&for=pc
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print('intercept = %s slope = %s' % (intercept, slope))

plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()