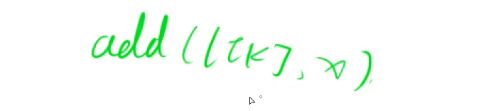算法基础值之单链表、双链表、栈、队列、单调栈、单调队列以及KMP
目录
- 1.单链表
-
- 1.1用数组模拟单链表
- 1.2 初始化
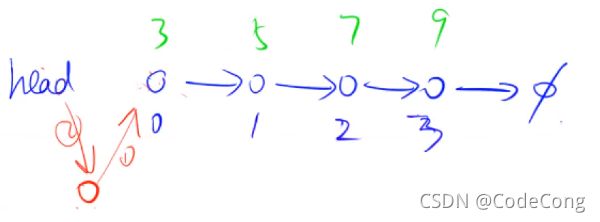
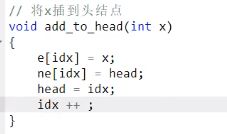
- 1.3 将x插入头结点
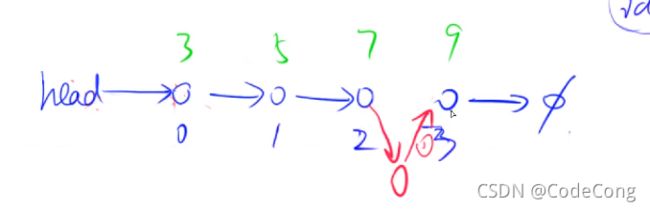
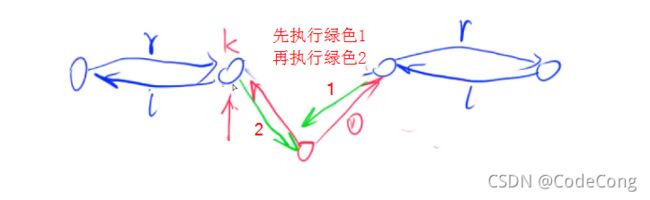
- 1.4 将x插入到k节点的后面
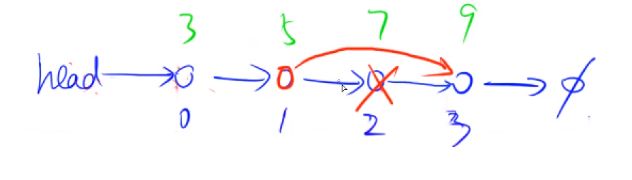
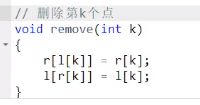
- 1.5 删除操作
- 1.6 单链表
- 2. 双链表
-
- 2.1 初始化
- 2.2 在一个节点的右边插入一个点
- 2.3 在一个节点的左边插入一个点
- 2.4 删除节点
- 2.5 代码
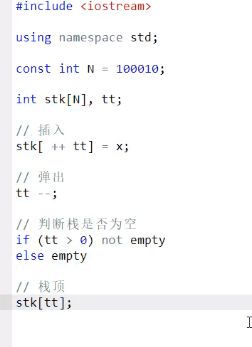
- 3.栈
-
- 3.1 表达式求值
- 4.队列
- 5. 考试考记忆力与自制力
- 6.单调栈
-
- 6.1考点
- 6.2 暴力做法
- 6.3 优化算法
- 6.4代码
- 7.单调队列(滑动窗口)
-
- 7.1 暴力做法
- 7.2 优化
- 7.3单调栈和单调队列的总结
- 8、KMP
-
- 8.1 什么是kmp以及暴力算法
- 8.2 模板串找最长后缀
- 8.3 主串与模板串的比较
- 8.4 kmp匹配过程代码(主串与模板串比较)
- 8.5 求next数组(模板串找最长后缀)
- 8.6 求next数组代码
- 8.7 kmp实现代码
1.单链表
1.1用数组模拟单链表
1.2 初始化
1.3 将x插入头结点
1.4 将x插入到k节点的后面
1.5 删除操作
1.6 单链表
#include 2. 双链表
2.1 初始化
2.2 在一个节点的右边插入一个点
2.3 在一个节点的左边插入一个点
2.4 删除节点
2.5 代码
#include 3.栈
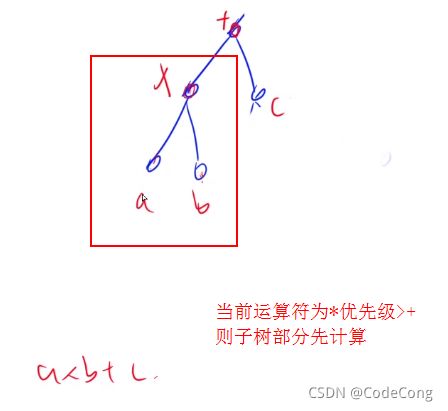
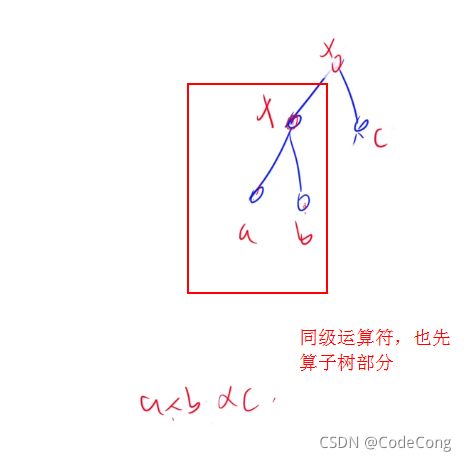
3.1 表达式求值
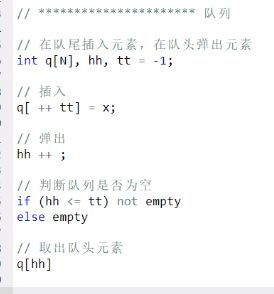
#include4.队列
5. 考试考记忆力与自制力
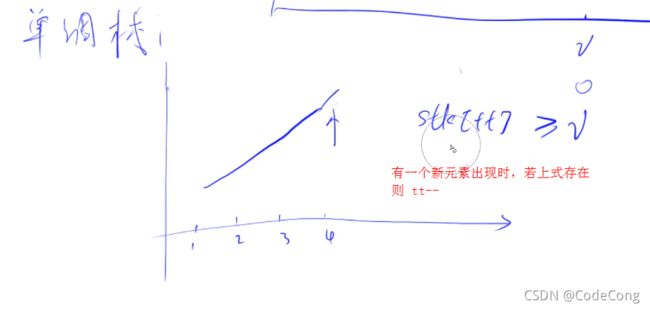
6.单调栈
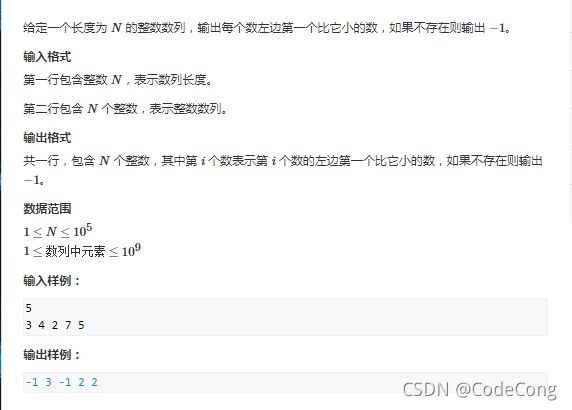
6.1考点
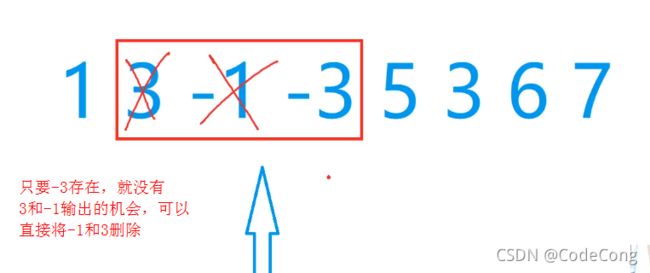
6.2 暴力做法
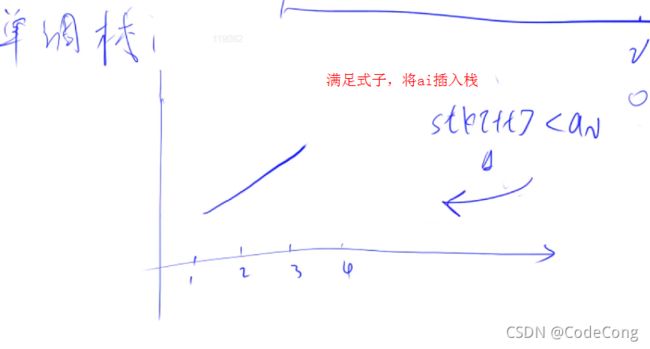
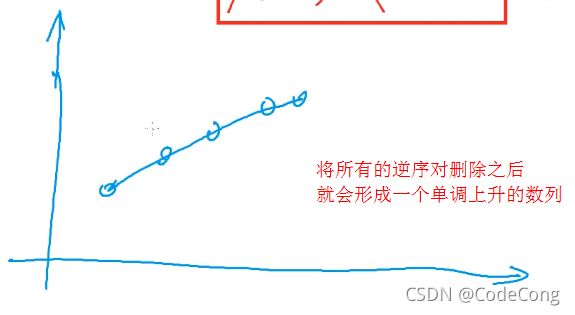
6.3 优化算法
6.4代码
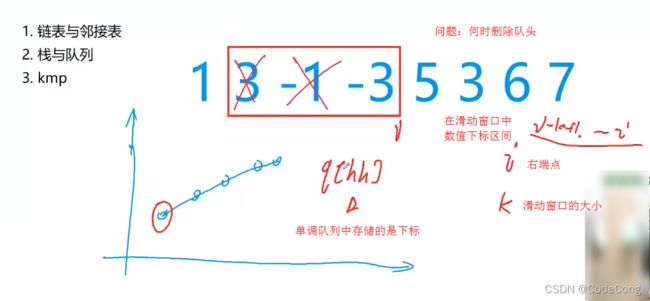
#include7.单调队列(滑动窗口)
7.1 暴力做法
保证每次存放与窗口大小相等的元素。
时间复杂度o(nk) 含有的元素个数n,窗口大小k。

7.2 优化
#include7.3单调栈和单调队列的总结
首先用栈和队列暴力的做法模拟算法。删除不必要的元素,观察新的元素是否具有单调性。可以通过取队头的方式找最大值和最小值。以及二分的方法查找某个元素。
8、KMP
8.1 什么是kmp以及暴力算法
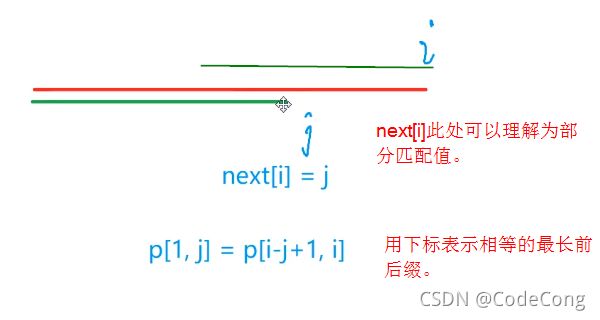
8.2 模板串找最长后缀
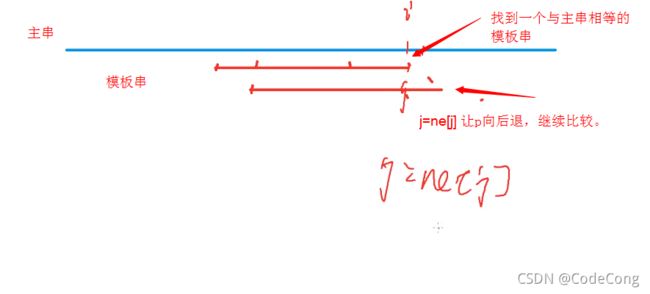
8.3 主串与模板串的比较
8.4 kmp匹配过程代码(主串与模板串比较)
for (int i = 1, j = 0; i <= m; i ++ )
{
//为什么j=0。是将s[i]与p[j+1]相比较,则p应该向前错一位,j=0
/*在比较过程中,当两者不想等时就让p向后退,
直到j=0时为止 */
//j不等于0->不为初始状态
//s[i]!=p[j+1] 红色圆和绿色圆不相等
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
//匹配成功
if (j == n)
{
printf("%d ", i - n);
//见图中的解释
j = ne[j];
}
}
8.5 求next数组(模板串找最长后缀)
图片模拟的是当p[i]!=p[j+1]时,p一直向后退的过程。
前提是在之前的比较过程中积累了最长后缀的数值。
这个过程也适合主串与模板串的比较过程。
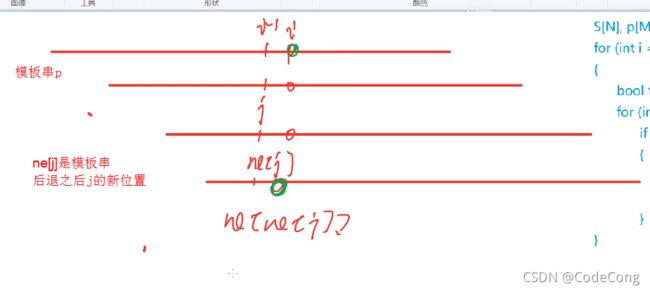
8.6 求next数组代码
//ne[1]=0 第一个字母失败了只能从头开始, 从2开始即可
for (int i = 2, j = 0; i <= n; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
8.7 kmp实现代码
#include