逻辑回归建立评分卡

在借贷场景中，评分卡是用分数形式来衡量一个客户信用风险的大小，分数越高代表信用风险越小。

针对个人客户而言，评分卡分为三类，分别是：
A卡（Application score card）申请评分卡
B卡（Behavior score card）行为评分卡
C卡（Collection score card）催收评分卡。

而众人常说的“评分卡”其实是指A卡，又称为申请者评级模型，主要应用于相关融资类业务中新用户的主体评级。
一个完整的模型开发，有以下流程：

获取数据

数据清洗

模型开发

模型检验与评估

模型上线

检测与报告

接下来，使用Give Me Some Credit数据集，总共15万条训练数据，介绍使用逻辑回归建立A卡的方法。

1 数据预处理

变量表：

变量名	变量解释
SeriousDlqin2yrs	是否有超过 90 天或更糟的逾期拖欠
RevolvingUtilizationOfUnsecuredLines	贷款以及信用卡可用额度与总额度比例
age	借款人的年龄
NumberOfTime30-59DaysPastDueNotWorse	35-59 天逾期但不糟糕次数
DebtRatio	负债比率
MonthlyIncome	月收入
NumberOfOpenCreditLinesAndLoans	未偿还贷款数量和信贷额度
NumberOfTimes90DaysLate	借款人逾期 90 天或以上的次数
NumberRealEstateLoansOrLines	不动产贷款或额度数量
NumberOfTime60-89DaysPastDueNotWorse	借款人已超过 60-89 天的次数，但在过去两年中没有更糟。
NumberOfDependents	家庭中的家属人数（配偶，子女等）

1.1 去重复值

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
import seaborn as sns
import scipy

data = pd.read_csv('cs-training.csv')
data = data.iloc[:,1:]
data.shape()
data.info()

data.drop_duplicates(inplace=True)
data.index = range(data.shape[0])

1.2 填补缺失值

观察缺失数据可以发现，需要填补的特征是“收入”和“家属人数”。“家属人数”缺失很少，仅缺失了大约2.5%，使用均值来填补。“收入”缺失了几乎20%，并且“收入”对信用评分来说是很重要的因素，因此使用随机森林填补“收入”。

data.isnull().sum()
data['NumberOfDependents'].fillna(int(data['NumberOfDependents'].mean()),inplace=True)

def fill_missing_rf(x,y,to_fill):
    df = x.copy()
    fill = df.loc[:,to_fill]
    df = pd.concat([df.loc[:,df.columns!=to_fill],pd.DataFrame(y)],axis=1)
    y_train = fill[fill.notnull()] 
    y_test = fill[fill.isnull()] 
    x_train = df.iloc[y_train.index,:] 
    x_test = df.iloc[y_test.index,:] 
    from sklearn.ensemble import RandomForestRegressor as rfr
    rfr = rfr(n_estimators=200,random_state=0,n_jobs=-1)
    rfr = rfr.fit(x_train,y_train)
    y_predict = rfr.predict(x_test)
    return y_predict

x = data.iloc[:,1:]
y = data['SeriousDlqin2yrs']

y_pred = fill_missing_rf(x,y,'MonthlyIncome')
data.loc[data.loc[:,'MonthlyIncome'].isnull(),'MonthlyIncome'] = y_pred

1.3 处理异常值

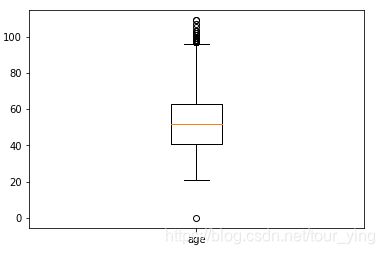
对于age变量，大于100岁小于等于0岁的可以认为是异常值，由箱线图可知，异常值样本不多，故直接删除

x1=data['age']
fig,axes = plt.subplots()
axes.boxplot(x1)
axes.set_xticklabels(['age'])

data = data[data['age']>0]
data = data[data['age']<100]

可以看到这三个变量都有明显的异常值

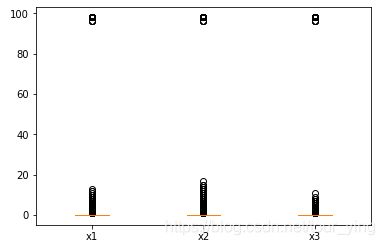
x1=data['NumberOfTime30-59DaysPastDueNotWorse']
x2=data['NumberOfTimes90DaysLate']
x3=data['NumberOfTime60-89DaysPastDueNotWorse']
fig,axes = plt.subplots()
axes.boxplot([x1,x2,x3])
axes.set_xticklabels(('x1','x2','x3'))

查看这三列的异常值，分别为96和98，把他们删除

data.loc[:,'NumberOfTime30-59DaysPastDueNotWorse'].value_counts()
data.loc[:,'NumberOfTimes90DaysLate'].value_counts()
data.loc[:,'NumberOfTime60-89DaysPastDueNotWorse'].value_counts()
data = data[data.loc[:,'NumberOfTime30-59DaysPastDueNotWorse']<90]
data.index=range(data.shape[0])

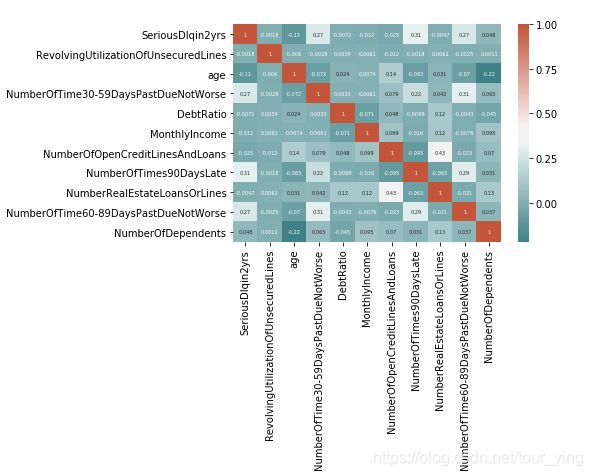
1.4 相关性分析

检验各个变量之间的相关性，如果各个变量之间拥有较强的相关性，会明显影响模型的泛化能力。
可以看出各变量间相关性较小，可进行后续建模。

corr = data.corr()
cmap = sns.diverging_palette(200,20,sep=20,as_cmap=True)
sns.heatmap(corr,annot=True,cmap=cmap,annot_kws={'size':5})

1.5 样本均衡处理

#查看两类标签比例
x = data.iloc[:,1:]
y = data.iloc[:,0]

grouped = data['SeriousDlqin2yrs'].groupby(data['SeriousDlqin2yrs']).count()
print('样本总数：{}，1占：{:.2%}，0占：{:.2%}'.format(x.shape[0],grouped[1]/x.shape[0],grouped[0]/x.shape[0]))
grouped.plot(kind='bar')

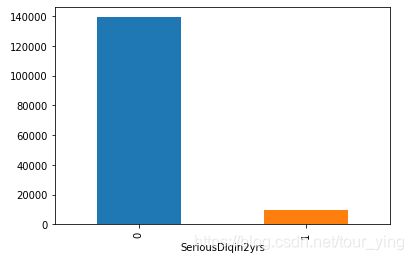
很明显，样本不均衡，样本总数：149152，1占：6.62%，0占：93.38%，这里采用上采样的方法来平衡样本。

from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state=0)
x,y = sm.fit_sample(x,y)

1.6 分训练集和测试集

from sklearn.model_selection import train_test_split
x = pd.DataFrame(x)
y = pd.DataFrame(y)

x_train,x_vali,y_train,y_vali = train_test_split(x,y,test_size=0.3,random_state=0)

model_data = pd.concat([y_train,x_train],axis=1)
model_data.index = range(model_data.shape[0])
model_data.columns = data.columns

vali_data = pd.concat([y_vali,x_vali],axis=1)
vali_data.index = range(vali_data.shape[0])
vali_data.columns = data.columns

2 特征处理

2.1 分箱

def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):
    DF = DF[[X,Y]].copy()
    DF["qcut"],bins = pd.qcut(DF[X],retbins=True,q=q,duplicates="drop")
    coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]
    coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]
    num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]
    # 确保每个箱中都有0和1
    for i in range(q):
        if 0 in num_bins[0][2:]:
            num_bins[0:2] = [(num_bins[0][0],num_bins[1][1],num_bins[0][2]+num_bins[1][2],num_bins[0][3]+num_bins[1][3])]
            continue
        for i in range(len(num_bins)):
            if 0 in num_bins[i][2:]:
                num_bins[i-1:i+1] = [(num_bins[i-1][0],num_bins[i][1],num_bins[i-1][2]+num_bins[i][2],num_bins[i-1][3]+num_bins[i][3])]
                break
        else:
            break
    #计算WOE
    def get_woe(num_bins):
        columns = ["min","max","count_0","count_1"]
        df = pd.DataFrame(num_bins,columns=columns)
        df["total"] = df.count_0 + df.count_1
        df["good%"] = df.count_0/df.count_0.sum()
        df["bad%"] = df.count_1/df.count_1.sum()
        df["woe"] = np.log(df["good%"] / df["bad%"])
        return df
    #计算IV值
    def get_iv(df):
        rate = df["good%"] - df["bad%"]
        iv = np.sum(rate * df.woe)
        return iv
    # 卡方检验，合并分箱
    IV = []
    axisx = []
    while len(num_bins) > n:
        pvs = []
        for i in range(len(num_bins)-1):
            x1 = num_bins[i][2:]
            x2 = num_bins[i+1][2:]
            pv = scipy.stats.chi2_contingency([x1,x2])[1]
            pvs.append(pv)
        i = pvs.index(max(pvs))
        num_bins[i:i+2] = [(num_bins[i][0],num_bins[i+1][1],num_bins[i][2]+num_bins[i+1][2],num_bins[i][3]+num_bins[i+1][3])]
        bins_df = pd.DataFrame(get_woe(num_bins))
        axisx.append(len(num_bins))
        IV.append(get_iv(bins_df))
    if graph:
        plt.figure()
        plt.plot(axisx,IV)
        plt.xticks(axisx)
        plt.xlabel("number of box")
        plt.ylabel("IV")
        plt.show()
    return bins_df

画出IV曲线，得到最佳分箱数

for i in model_data.columns[1:-1]:
    print(i)
    graphforbestbin(model_data,i,'SeriousDlqin2yrs',n=2,q=20,graph=True)

以DebtRatio为例，根据IV值的变化幅度由大变小的点，选择最佳分箱数为4，其他变量以此类推。

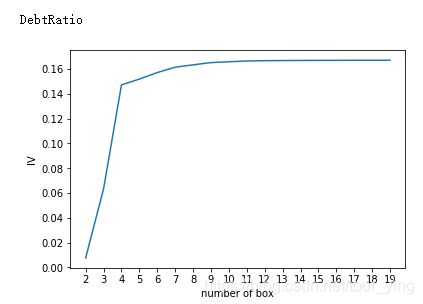
根据IV曲线找出的分箱结果如下：

auto_bins = {'RevolvingUtilizationOfUnsecuredLines':5
            ,'age':6
            ,'DebtRatio':4
            ,'MonthlyIncome':3
            ,'NumberOfOpenCreditLinesAndLoans':7
            }

但不是所有特征都能用这个方法，不能自动分箱的变量可以对变量进行观察手动分箱。

# 以下变量手动分箱
hand_bins = {'NumberOfTime30-59DaysPastDueNotWorse':[0,1,2,13]
            ,'NumberOfTimes90DaysLate':[0,1,2,17]
            ,'NumberRealEstateLoansOrLines':[0,1,2,4,54]
            ,'NumberOfTime60-89DaysPastDueNotWorse':[0,1,2,8]
            ,'NumberOfDependents':[0,1,2,3]
            }

# 用-np.inf,np.inf替换最小值和最大值
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}

# 对所有特征分箱：
bins_of_col = {}
for col in auto_bins:
    bins_df = graphforbestbin(model_data,col,'SeriousDlqin2yrs',n = auto_bins[col],q=20,graph=False)
    bins_list = sorted(set(bins_df['min']).union(bins_df['max']))
    #保证区间覆盖使用np.inf替换最大值-np.inf替换最小值
    bins_list[0],bins_list[-1] = -np.inf,np.inf
    bins_of_col[col] = bins_list

# 合并手动分箱的结果
bins_of_col.update(hand_bins)
bins_of_col 

2.2 计算WOE、IV值

def get_woe(df,col,y,bins):
    df = df[[col,y]].copy()
    df["cut"] = pd.cut(df[col],bins) 
    bins_df = df.groupby("cut")[y].value_counts().unstack()
    woe = bins_df["woe"] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
    iv = np.sum((bins_df[0]/bins_df[0].sum()-bins_df[1]/bins_df[1].sum())*bins_df['woe'])
    return woe
    #return iv

woeall = {}
#IV = {}
for col in bins_of_col:
    woeall[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])
    #IV[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])

画出各特征的IV值

index = ['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
index_num = range(len(index))
plt.figure()
plt.bar(index,IV.values())
plt.show()

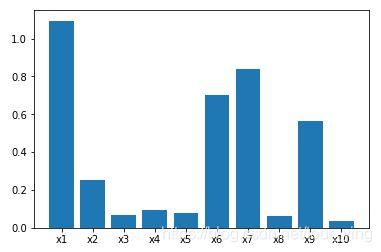
x1 ‘RevolvingUtilizationOfUnsecuredLines’: 1.0949541172484247,
x2 ‘age’: 0.2503443210341437,
x3 ‘DebtRatio’: 0.06638925056198089,
x4 ‘MonthlyIncome’: 0.09548586296415988,
x5 ‘NumberOfOpenCreditLinesAndLoans’: 0.07991090090702914,
x6 ‘NumberOfTime30-59DaysPastDueNotWorse’: 0.7020812947616354,
x7 ‘NumberOfTimes90DaysLate’: 0.8396562353357999,
x8 ‘NumberRealEstateLoansOrLines’: 0.06350368034698911,
x9 ‘NumberOfTime60-89DaysPastDueNotWorse’: 0.5623219236223598,
x10 ‘NumberOfDependents’: 0.03414718377941136}
一般认为，IV值小于0.03的特征几乎不带有有效信息，对模型没有贡献，可以删除，这组特征中最低值为’NumberOfDependents’为0.034，所有特征都可以保留。

接下来，将WOE映射到原始数据中，形成建模数据。

model_woe = pd.DataFrame(index=model_data.index)

for col in bins_of_col:
    model_woe[col] = pd.cut(model_data[col],bins_of_col[col]).map(woeall[col])

model_woe["SeriousDlqin2yrs"] = model_data["SeriousDlqin2yrs"]
model_woe  #这就是建模数据

3 模型建立

计算测试集vali_woe,利用建立好了的get_woe函数:

woeall_vali = {}
for col in bins_of_col:
    woeall_vali[col] = get_woe(vali_data,col,"SeriousDlqin2yrs",bins_of_col[col])
    
vali_woe = pd.DataFrame(index=vali_data.index)
for col in bins_of_col:
    vali_woe[col] = pd.cut(vali_data[col],bins_of_col[col]).map(woeall_vali[col])

vali_woe["SeriousDlqin2yrs"] = vali_data["SeriousDlqin2yrs"]
vali_x = vali_woe.iloc[:,:-1]
vali_y = vali_woe.iloc[:,-1]

接下来就可以建模了

from sklearn.linear_model import LogisticRegression as LR
x = model_woe.iloc[:,:-1]
y = model_woe.iloc[:,-1]
lr = LR().fit(x,y)
lr.score(vali_x,vali_y)

模型得分为0.8652

混淆矩阵

from sklearn.metrics import confusion_matrix
C2 = confusion_matrix(y_true,y_pred)
sns.heatmap(C2,annot=True,fmt='d')

准确率 = TP \ (TP+FP) = 0.85
召回率 = TP \ (TP+FN) = 0.89

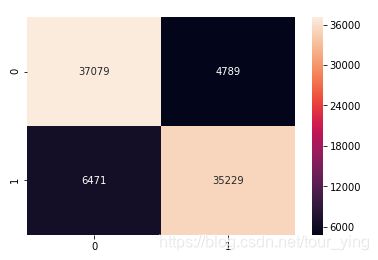
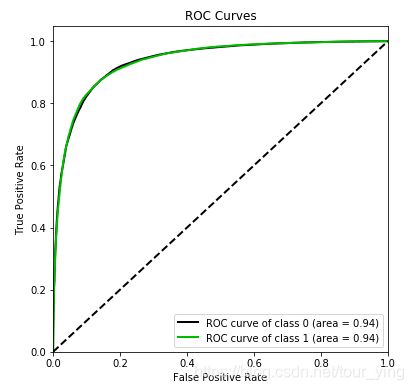
绘制ROC曲线，ROC=0.94，曲线越往左上凸，True Positive 就越高，对应的False Positive越低。

import scikitplot as skplt
vali_proba_df = pd.DataFrame(lr.predict_proba(vali_x))
skplt.metrics.plot_roc(vali_y,vali_proba_df,
                      plot_micro=False,figsize=(6,6),
                      plot_macro=False)

4 制作评分卡

求出A、B和base_score
将所有特征的评分卡内容全部一次性写往一个本地文件ScoreData.csv：

with open(file,"w") as fdata:
    fdata.write("base_score,{}\n".format(base_score))
for i,col in enumerate(x.columns):
    score = woeall[col] * (-B*lr.coef_[0][i])
    score.name = "Score"
    score.index.name = col
    score.to_csv(file,header=True,mode="a")