剑指offer——JZ7 重建二叉树 解题思路与具体代码【C++】

一、题目描述与要求

重建二叉树_牛客题霸_牛客网 (nowcoder.com)

题目描述

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。

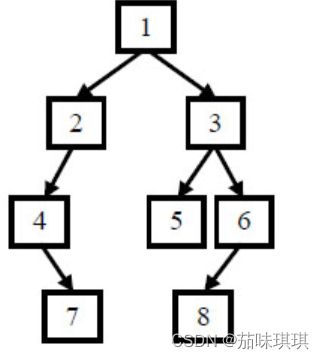
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

提示:

1.vin.length == pre.length

2.pre 和 vin 均无重复元素

3.vin出现的元素均出现在 pre里

4.只需要返回根结点，系统会自动输出整颗树做答案对比

数据范围：n≤2000，节点的值 −10000≤val≤10000

要求：空间复杂度 O(n)，时间复杂度O(n)

示例

示例1：

输入：[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]

返回值：{1,2,3,4,#,5,6,#,7,#,#,8}

说明：返回根节点，系统会输出整颗二叉树对比结果，重建结果如题面图示

示例2：

输入：[1],[1]

返回值：{1}

示例3：

输入：[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]

返回值：{1,2,5,3,4,6,7}

---

二、解题思路

根据题目描述，给出我们一个二叉树的前序遍历与中序遍历结果来还原重建二叉树，首先我们需要了解前序遍历与中序遍历其中的规律，这样才能够通过遍历结果来还原原本的二叉树。

前序遍历——先输出根结点，然后先序遍历左子树，再先序遍历右子树。

中序遍历——中序遍历左子树，输出根结点，然后中序遍历右子树。

由此可以知道前序遍历的第一个结点就是整个二叉树的根结点，然后在中序遍历中找到这个根结点，我们就可以将遍历结果进行划分，中序遍历的前半部分就是根结点的左子树的中序遍历结果，右半部分就是根结点的右子树的中序遍历结果，同时也可以对前序遍历进行划分，前半部分为左子树的前序遍历结果，后半部分为右子树的前序遍历结果。以此来再对左子树和右子树进行相同的处理（递归），一直到遍历序列的长度为0，则结束，同时二叉树也就建立完成。

首先我们获取两个遍历结果序列的长度（用于判断是否遍历结束）。

然后利用前序遍历第一个结点来构造根结点。

然后就是在中序遍历序列中找到对应的根结点，然后将两个遍历序列进行划分成左右两部分，分别用来构造左子树和右子树。if语句末尾加上break是防止for循环继续下去浪费时间。

最后返回root即可。

---

三、具体代码

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param preOrder int整型vector 
     * @param vinOrder int整型vector 
     * @return TreeNode类
     */
    TreeNode* reConstructBinaryTree(vector& preOrder, vector& vinOrder) {
        int n=preOrder.size();
        int m=vinOrder.size();
        //每个遍历都不能为0
        if(n==0||m==0){
            return nullptr;
        }
        //构造根结点
        TreeNode* root=new TreeNode(preOrder[0]);//前序遍历第一个结点就是根结点
        for(int i=0;i leftpre(preOrder.begin()+1,preOrder.begin()+i+1);
                //左子树的中序遍历
                vector leftvin(vinOrder.begin(),vinOrder.begin()+i);
                //构建左子树
                root->left=reConstructBinaryTree(leftpre, leftvin);
                //右子树的前序遍历
                vector rightpre(preOrder.begin()+i+1,preOrder.end());
                //右子树的中序遍历
                vector rightvin(vinOrder.begin()+i+1,vinOrder.end());
                //构建右子树
                root->right=reConstructBinaryTree(rightpre, rightvin);
                break;
            }
        }
        return root;
    }
};