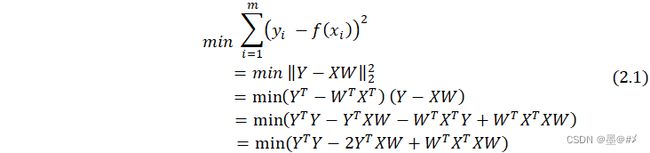关于最小二乘拟合与正则化的探讨

说明

    最小二乘法是一个应用领域很广，且很常用的数学工具，所以网上关于最小二乘法的文章资料有很多(在参考资料中附上了几篇读者可以进一步参考)。本博文想要探讨该话题的出发点源于上一篇博文：车载毫米波雷达的上车安装与标定问题_墨@#≯的博客-CSDN博客，文中有提到使用最小二乘法来拟合道路边沿，进而确定雷达安装的角度误差并完成雷达水平角的标定，于是想要对最小二乘法做一些有益的学习和解释。

    最小二乘法背后的拟合思想(欠拟合、过拟合现象及其解决)可以一直延伸到机器学习领域(最小二乘拟合是机器学习最基础的内容之一)，囿于本人现阶段的学识水平，本博文目前只对最小二乘法做初步的探讨。

Blog

20230917 博文第一次撰写

目录

目录

说明

目录

一、最小二乘法的基本概念

二、拟合函数求解方法

2.1 代数求解方法

2.2 使用Matlab自带的函数

三、仿真与讨论

3.1 仿真结果及其讨论

3.2 关于过拟合问题

3.2.1 过拟合问题的原因探讨

3.2.2 针对前述原因的仿真验证

3.2.3 正则化问题讨论

四、总结

五、参考资料

六、参考代码

---

一、最小二乘法的基本概念

    最小二乘法是一个数学工具。是指：一种在现有(观测)数据的基础上基于 最小化误差的平方和 的原则进行函数拟合的方法。这句话用数学语言来描述就是：

    假设有n组观测数据：（xi, yi），(i = 1,2,3,4…n)，我们现在要求得一个函数：

                                    (1.1)

    式中，是事先选定的一组线性无关的函数，是待定系数(k = 0，1,2,3… m)。使得：

                                                                                            (1.2)

    L的值最小。这便是最小二乘法以及它要解决的问题。

    在得到该拟合后的函数后，我们也就得到了一条曲线，这条曲线可以被用来做很多事情：比如做误差估计、做预测、求路沿斜率以做标定用(上一篇雷达安装与标定博文中的内容)、求目标运动轨迹的曲率(毫米波雷达SOR中一般也要求雷达可以输出目标运动轨迹的曲率)、以及基于车载传感器做自由空间映射(Freespace)时，如果有路沿我们可以用以拟合路沿(当然，这和前面求路沿的斜率其实是一件事… 我这里只是想强行引出Freespace这个词：基于车载环境感知传感器的Freespace算是一个比较新的概念？我后续会出一期调研的博文聊聊这个话题)，等等。

*需要注意的是*

1、事实上，基于离散的点做曲线拟合方法(基准)可以有很多，比如你可以使得拟合得到的曲线到各观测点(待拟合点)的距离之和最小，或者使各观测点到拟合曲线的最大距离取最小值等等，甚至你自己可以提出一些拟合的基准。但是，最小二乘法(使得各观测点到拟合曲线的偏差的平方和最小)这个基准被证明是误差符合高斯分布时的最佳线性无偏估计,该方法下得到的估测误差也是呈正态分布的(高斯最早证明了，关于最小二乘拟合这个方法的发明，高斯和勒让德之间有一段蛮有意思的历史故事，感兴趣的可以去搜索了解。)

2、做拟合时，我们一般是用多项式进行拟合，所以f(x)实际上应该是：

                                                 (1.3)       

（多项式是曲线的“最小单元”？有点类似三角函数sin（x）是各种波形的“最小单元”）

3、最小二乘法拟合得到的函数(以及曲线)其实只对用来拟合的观测点以及观测点对应的观测区间负责，如果想要用以预测观测区间之外的点，那么有两个很重要的条件：a.观测区间外的点和观测点之间是要有连续性关系的；b.所拟合的多项式阶数一定要选正确(避免出现欠拟合或者过拟合的情况)。

4、曲线拟合最关键的在于拟合曲线的多项式阶数的选取。

5、关于第3、4点，我会在后文用仿真结果来作出解释。

二、拟合函数求解方法

2.1 代数求解方法

    由前述式(1.2)，我们可以得到：

                                      

    式中，Y为n*1大小列向量，对应观测点的y值，X为n*m大小的矩阵，W为代求系数向量，大小为m*1，m的大小对应所选阶数的值。该式对W求偏导并使其为0(极值点)，便可得到W的解析解。

                                                                (2.2)

    于是：

                                                                                                          (2.3)

    由该式得到的系数构造对应的多项式函数，进而可得到拟合的曲线。（不过需要说明的是，从公式可以看到，该W值可以被求解的充分条件是是可逆的，也即X的列向量之间应该是线性无关的）。

2.2 使用Matlab自带的函数

    如此通用且具备确定计算公式和解的方法自然很容易写成函数，使用时直接调用即可。Matlab自带的做最小二乘拟合的函数为：polyfit与polyval。这两函数更多的使用细节读者可以去Matlab的帮助文档里阅读，这里给出这两函数实现拟合最基本的输入输出以及使用方法(凑字数..)。

    [P，S，mu] = polyfit(x,y,n)；用以输入观测值和想要拟合的阶数，该函数可以输出拟合得到的系数值。

输入：x和y为观测点对应的坐标值，n表示设定的拟合函数最高的阶数值。

输出：P为拟合后多项式的系数(按降幂排序，从x^n的系数到x^0的系数，所以该数组一共会有n+1个值)。mu为可选输出项，其值为一个含两个元素的向量，mu(1)为输入x的均值，mu(2)为x的标准差。S为可选输出项，是一个结构体，细节读者可以看帮助文档。一般使用时输出P即可。

    [y,delta] = polyval(P，x，S，mu)；用以输入系数和想要查看的坐标值x，得到该套多项式系数下在这些坐标值x下的y值。

输入：P为ployfit得到的多项式系数，x为在该系数下想要计算的点的横坐标值(这个值可以是观测区间乃至观测区间以外的所有值)，S和mu为可选输入项，对应前述polyfit的可选输出项。

输出：y为在系数P和x值下该拟合得到的函数纵坐标值，delta为可选输出项，其值为每个x值输出y值的标准误差，大小等于x，一般地，y±delta的区间置信度(当我们用这条曲线去做区间内的值的预测时)为68%，y±2*delta的区间置信度为95%，具体的可以看帮助文档。一般在使用时输出y即可。需要注意的是，如果在polyfit中要求输出mu这个参数，那么在使用polyval计算y时也需要将之放在输入参数里，否则会有一些问题。

三、仿真与讨论

    本章通过仿真来实践最小二乘拟合问题，并做一些有益的探讨。本章的仿真和行文思路大概是：设计一个函数，并生成坐标点  ---->   对坐标点加噪声  ----> 用最小二乘法拟合这些加噪声后的点(设计不同的迭代次数，并将之与原始函数做比较)  ---->  讨论欠/过拟合问题   ---->  讨论过拟合问题的解决办法。

3.1 仿真结果及其讨论

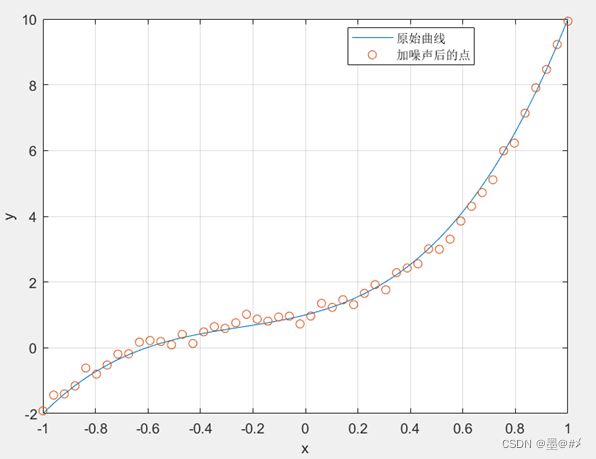
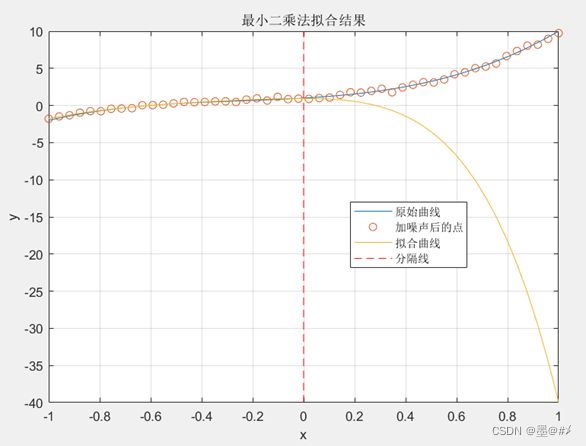
    本次仿真选用了三阶函数：y = 4.*x.^3 + 3.*x.^2 + 2.*x + 1 作为原始曲线，并在[-1 1]区间内均匀选取了50个点加SNR为15dB的高斯白噪声作为观测点。结果如下图所示：

图3.1  原始曲线&加噪声后的观测点

    为方便后续关于欠/过拟合问题的说明，我选取了区间[-1 0]内的观测点作为“训练集”进行拟合，并将[0 1]内的观测点作为判断是否过拟合的“验证集”。

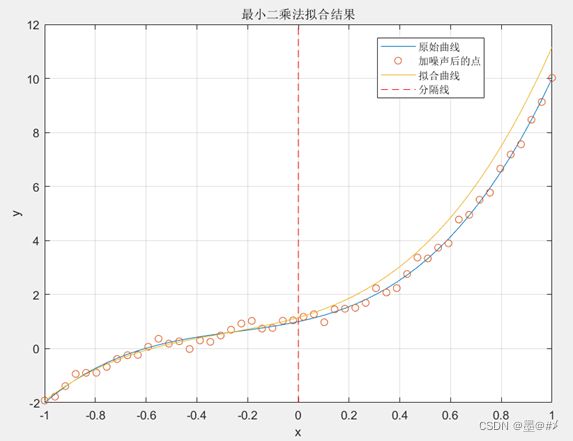
    当使用最高三阶多项式的函数进行拟合时，效果如下：

图3.2  使用最高3阶多项式函数进行拟合时的拟合结果

    由上图可以看到，效果还OK，特别是[-1 0]区间内的拟合效果(只是选取了该区间内的观测数据进行拟合)。当使用最高1阶多项式的函数进行拟合时，效果如下：

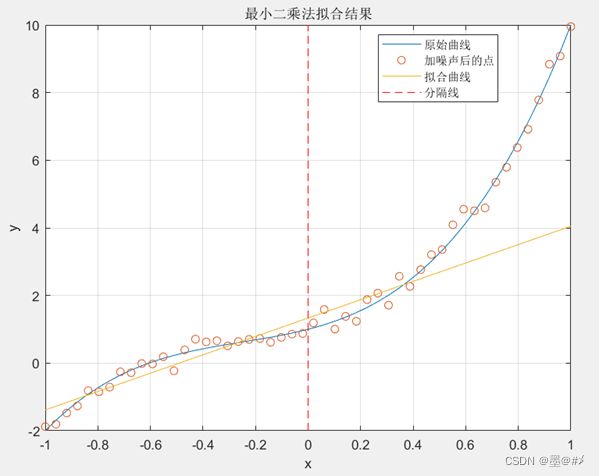
图3.3  使用最高1阶多项式函数进行拟合时的拟合结果

    从图中可以看到，不管是[-1 0]区间还是[0 1]区间，拟合的效果是很差的，这便是所谓的欠拟合现象。当使用最高5阶多项式的函数进行拟合时，得到的拟合结果如下：

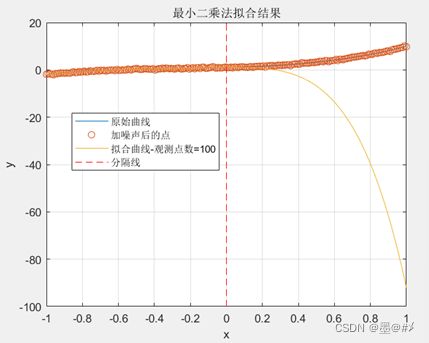
图3.4  使用最高5阶多项式函数进行拟合时的拟合结果1

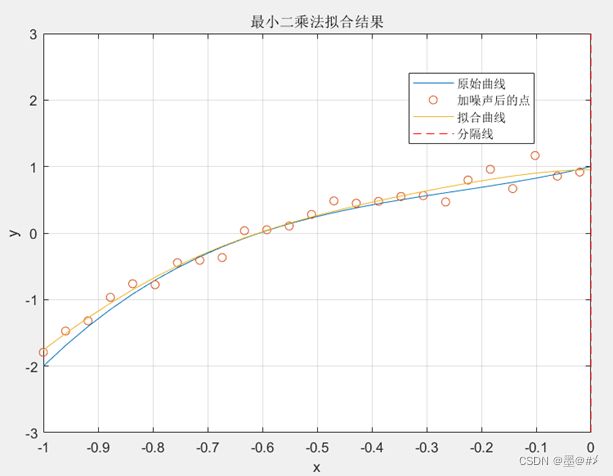
    从上图可以看到，[0 1]区间内已经完全背离了，不具备“预测”效果。但是[-1 0]区间的拟合结果其实很好：

图3.5  使用最高5阶多项式函数进行拟合时的拟合结果2

    甚至看起来比原始曲线更贴近观测点，这便是过拟合现象：很符合“训练”数据，但是对于测试集来说差很远。

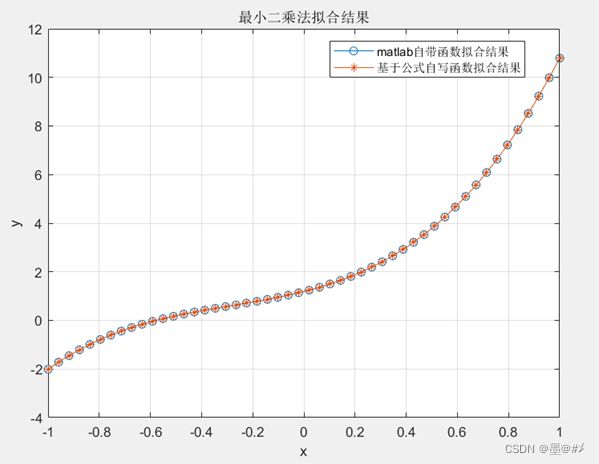
    仿真中我也尝试了基于公式(2.3)进行拟合，效果一样(不管是设置在几阶之下)，下图为3阶下的两种方法拟合结果对比：

图3.6  基于公式(2.3)的拟合与Matlab自带函数的拟合结果对比

    函数的实现其实很简单(不管是基于公式(2.3)写函数，还是基于Matlab自带的函数进行仿真)，读者可以参考本文随附的参考代码。

*对前述结果进行小结*

1、实践了最小二乘拟合法(分别基于Matlab自带的函数以及基于公式(2.3)自写函数)。

2、最小二乘拟合法最关键的在于阶数的选取，这从前面不同阶下的仿真结果对比可以看出：只有当使用三阶函数时拟合的效果最好。当阶数选取不对时，会产生欠拟合或过拟合现象。

3、最小二乘拟合从某种程度上来说只对拟合区间内的内容负责。只有当观测区域外的区间与观测数据之间具备特定的关系(比如同为某一个函数)且拟合时所使用的阶数比较好地契合了这个函数时，拟合曲线对区间外的数据拟合效果较好。

4、以上结论闭环了第一章中的注意点。

3.2 关于过拟合问题

3.2.1 过拟合问题的原因探讨

    最小二乘拟合应用在说明中提到的道路边沿拟合，或者雷达检测目标轨迹的曲率计算时，一般不会存在欠/过拟合问题，因为我们事先知道要拟合的东西是什么：我们一般用一阶多项式函数(直线)去拟合做标定时的路沿，用二阶多项式函数拟合目标运动轨迹。欠或者过拟合现象主要出现在我们无法确定应该使用多高的阶数去拟合观测数据时的情况，这两个概念现阶段主要的适用领域还是机器学习，关于计算机我了解不多，本小节对这两个概念只做一点简单解释。

    我们用作拟合的数据是观测数据，这些数据并不是完全真实的、正确的，它是有噪声(各种原因导致数据失真)的，此时如果阶数过高，会导致拟合得到的曲线完全符合观测数据，也即曲线把噪声等错误信息也学进去了，这便是过拟合。

    产生过拟合问题的本质大概可以归纳为：模型太过复杂(阶数太高)、数据精度不够、数据数量不够。以下对这几个原因进行仿真验证。

3.2.2 针对前述原因的仿真验证

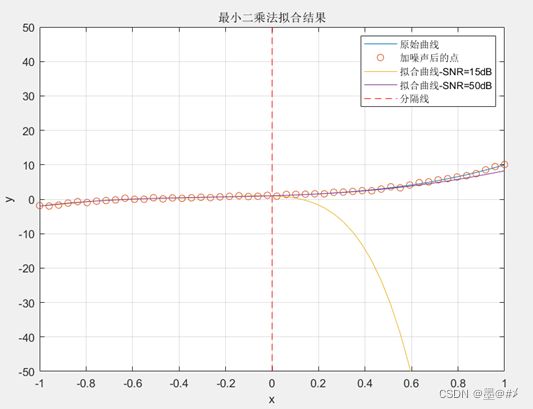
    按照前面的结论，这里假设提高SNR，看看过拟合的现象是否得到有效改善(从之前的15dB，改成50dB)：

图3.7  不同SNR的观测数据下，5阶多项式函数的拟合结果对比

    可以看到，过拟合的现象消失了(得到很大改善)！同时，也试验一下在SNR同为15dB的前提下，增加[-1 0]区间内的点数，从原来的25个点增加到100个点，继续用5阶多项式进行拟合：

  

图3.8  不同“训练”(观测)点数下的拟合结果1

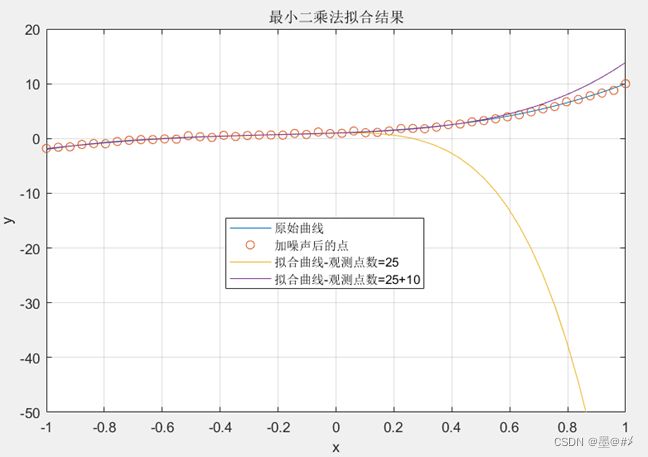
    在相同的SNR下，增加[-1 0]区间内的点数并只使用该区间内的观测点进行拟合时，对过拟合现象的改善并不明显。当我们把观测(训练)区间扩大时，应该才有效果，下图的仿真中我们并没有增加全区域内的点数，但是把“训练”区间扩大，从[-1 0]的基础上往外增加了10个点，得到的仿真结果如下：

图3.9  不同“训练”(观测)点数下的拟合结果2

    从图中可以看到，得益于观测区间的扩大(带来的点数的增多)，此时的过拟合现象也消失(得到很大改善)了。阶数过高引起的过拟合现象已经在上一节中有充分的说明和证明，本节不做赘述。综上，我们仿真论证了可以通过增加数据精度以及基于扩展训练区间的方式增加数据量来抑制过拟合现象。

3.2.3 正则化问题讨论

    但是，一般来说，数据精度和数据量是我们做拟合时没法控制的(我们只是拿到给的观测数据去做拟合，数据的精度和数量我们没法控制)，此时，我们只能通过控制模型的复杂度来解决过拟合问题。

    控制模型复杂度来降低过拟合对应到曲线拟合最直接的方法自然就是降低多项式的阶数。可是，降低到多少才是合适的？(会不会导致欠拟合？)，有没有一种方法，在我们不改变阶数的前提下，通过控制比如高阶项的系数来缓解过拟合问题？(因为由于模型太过高阶导致的过拟合现象其本质就是不应该有这些高阶项，其系数应该越小越好)

    人们针对该问题发明了正则化的方法：通过在最小二乘的平方和最小准则中引入正则化项来控制多项式的系数：

        (3.1)

    式中，就是我们引入的正则化项(λ为正则化值，W代表的还是多项式的系数)。正则化是指在原有约束关系的基础上增加各类范数(所谓的惩罚项)来配合约束。向量范数是我们用来表征向量空间中距离的一种方式，我们有各种范数的定义，比如1-范数，是将向量中各值的绝对值相加，2-范数，是将向量中各值的平方和相加后再开方。我们也可以由(3.1)推导得到W的解析解，比如对于2-范数，我们可以得到：

                                                                                    (3.2)               

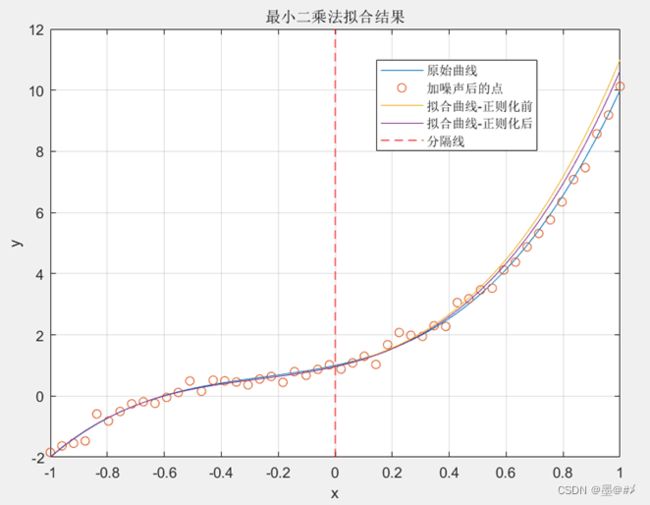
    推导的方法与前文类似，在该公式的指导下，分别对原始的3阶多项式函数进行3阶和6阶下的拟合并与没有正则化下的情况进行对比：

图3.10  正则化前后对比1(最高阶为3阶)

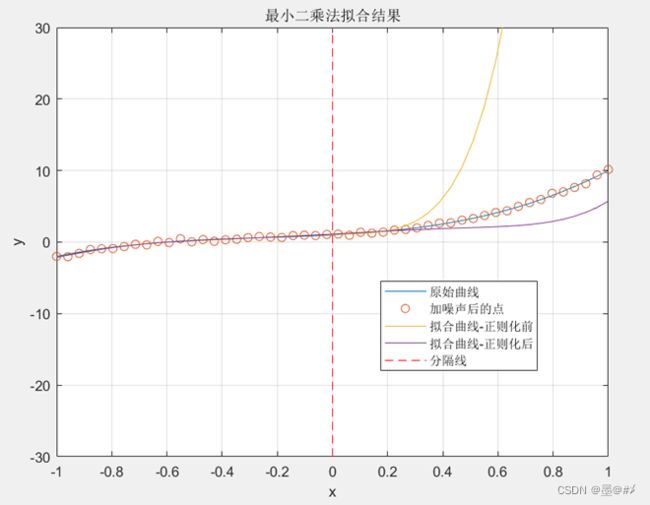
图3.11  正则化前后对比2(最高阶为6阶)

    仿真中，λ的值取为0.001(读者可以基于我提供的代码进行不同系数下的仿真对比)，从上面两图的结果来看，正则化后，效果得到明显改善。

    总之，在正则化后，由于所选阶数过高而导致的过拟合问题可以得到有效缓解，机器学习领域中如何去更好地设计该正则化项是研究的重点之一。

四、总结

    最小二乘拟合法是一个很常用(且很通用)的数学工具，本博文介绍了最小二乘拟合的相关概念与原理，随后分别基于代数求解和Matlab自带函数两种方式仿真实践了该方法，并做了一些有益的讨论，特别是关于过拟合问题。

    本文内容相对简单，不过通读本文后应付一些相关的拟合问题应该难度不大。关于本话题更深入的一些探讨读者可以进一步搜寻相关资料，在后续的工作和学习中如果有涉及到该问题我也会不定期对本文做补充。

五、参考资料

1、最小二乘拟合，L1、L2正则化约束_matlab l2正则化代码_there2belief的博客-CSDN博客

2、详解岭回归与L2正则化_岭回归和正则化_胤风的博客-CSDN博客

3、深度学习基础算法系列（3）-正则化之L1/L2正则化 - 知乎 (zhihu.com)

六、参考代码

关于最小二乘拟合法的探讨博文相对应的代码资源-CSDN文库