2022年华中杯数学建模挑战赛A题分拣系统优化问题求解全过程文档及程序

2022年华中杯数学建模

A 题 分拣系统优化问题

原题再现：

  某电商公司配送中心的工作流程分为统计汇总、转运上架、按订单分拣、核对打包等步骤。其中，分拣环节操作复杂，耗时较长，其效率是影响配送中心整体性能的关键因素。
  首先，系统统计汇总出当天全部待配送订单所包含的所有货品及相应数量。然后，转运工将这些货品由仓库转运至分拣处，并放置到货架上，等待分拣。上架时，一个货架中仅放置同一种货品。为简化问题，不考虑货架的容积和载重限制，即每个货架能够放置的货品件数没有限制。最后，分拣工按任务单依次分拣出每一个订单包含的货品。例如，某天共有 5 个订单，订单的信息如表 1（原始数据文件格式见附件 1 格式说明）所示。
  表 1：订单信息示例
订单编号    所含货品种类及相应数量
D0001     P0001×2, P0002×1, P0003×1, P0004×1
D0002     P0003×1, P0004×1, P0005×1, P0006×3
D0003     P0001×1, P0003×1, P0005×1, P0007×1
D0004     P0002×1, P0004×1, P0006×1, P0008×3
D0005     P0001×1, P0003×2, P0004×1, P0007×1
  系统统计出这 5 个订单共包含 8 种 26 件货品，分别为 4 件 P0001、2 件 P0002、5 件
P0003、4 件 P0004、2 件 P0005、4 件 P0006、2 件 P0007 和 3 件 P0008。转运工将这些货
品分别放置在 8 个货架上。分拣工根据任务单上的订单信息，依次分拣出每一个订单的货品。
  随着该公司业务量不断增长，未来有可能出现当天待配送订单所含货品种类数大于当前货架数量的情况（假设任何一个订单所含货品种类数均小于货架数量 ）。但是，由于受到场地和成本的限制，很难直接增加货架。该公司希望在你们团队的协助下解决该问题，并尝试提高分拣效率。具体解决如下问题。
  1. 设计分批算法：将当日订单分为多个批次。要求每个批次的订单所含货品种类数均不超过 ，且批次越少越好（相应转运次数也越少，效率越高）。针对附件 1 中的订单信息，应用你们的算法，计算当货架数量 时最少的批次数，给出每批订单数量、货品种类数、分批方案等结果，并将完整原始分批方案按指定格式输出到文件result1.csv 中，格式要求见附件 2。
  2. 优化货品摆放位置：确定每一种货品放置在哪一个货架。分拣工拣选货品时，同一订
单所含货品的位置越集中，移动距离越短，拣选效率越高。分拣处简化布局示意图如
图 1。假设所有货架等距排列在一条直线上，按照摆放位置的顺序，货架的序号依次
为1，2，3，…，N ，货品i所在货架的序号为S(i) 。某一订单Qk的拣选距离定义为该订
单中货品所在货架序号的最大值与最小值之差，即：

  对于给定的某一批分拣任务，请设计货品摆放算法，使得该批分拣任务所有订单的拣选距离总和尽量小。并针对附件 1 的数据，在第 1 问得到的分批结果基础上，考虑拣选距离，设计各批次中每一种货品的摆放位置，给出各批分拣任务的拣选距离总和，以及所有批次全部订单的拣选距离总和，并将完整原始货品摆放方案按指定格式输出到文件 result2.csv 中，格式要求见附件 3。

  3. 指派分拣任务：按批次将所有订单分配给多个分拣工并行完成分拣任务。假设：
    1) 分拣工在分拣过程中互相不会干扰，即运动路线不会冲突，也可以同时拣选同一货架上的货品。
    2) 一位分拣工同一时间只能处理一个订单，即一位分拣工完成一个订单的分拣工作之后，才能开始下一个订单的分拣工作。
    3) 每位分拣工在自己的分拣任务完成之前，始终匀速运动，忽略从货架上取货所需的时间，忽略订单之间的切换时间，忽略休息时间，且所有分拣工的运动速度相同。
    4) 结合前一个假设，一位分拣工在处理当前订单时，只要经过该订单中某一货品所在货架至少一次，就视为已经拣选到该货品。
    5) 拣选到的货品放入拣货筐中，同一订单的货品放入同一个拣货筐中，不考虑拣货筐容量限制。一个订单的货品全部拣齐后，分拣工将该筐放上传送带，自动转移至核对打包环节，之后可立即原地取用一个新的空的拣货筐。忽略放置拣货筐、取用新筐的时间。
    6) 在每一批分拣任务开始前，每位分拣工领取到自己当前批次的任务单，需要按照任务单上的订单顺序，依次完成所有订单的分拣工作。同一订单中的不同货品不区分拣货顺序，由分拣工按照最优方式决定。
    7) 在每一批分拣任务开始时，所有分拣工位于 1 号货架处，同时由 1 号货架出发，开始当前批次的分拣工作。每位分拣工完成一个订单之后，可以立即开始下一个订单的分拣工作，不需要回到 1 号货架。分拣工在拣选完当前批次自己任务单上所有订单的货品后，回到 1 号货架，完成当前批次任务，休息，等待下一批分拣任务开始。
    8) 假设不考虑货架的几何尺寸，相邻两个货架间的距离均为单位 1，结合上述假设，某一分拣工分拣完成任务单上所有订单所需时间与其运动总距离呈正比。对于给定的某一批分拣任务，且货品摆放位置已知，请设计订单指派算法，将分拣任务分配给n位分拣工，使得能够尽快完成任务，且运动距离尽可能均衡。针对附件 1 的数据，在前两问的基础上，当分拣工人数 时，计算各批次中订单的指派结果及每一位分拣工处理订单的顺序，并将完整原始指派方案按指定格式输出到文件 result3.csv 中，格式要求见附件 4。
    附件 1：订单信息
    格式说明：
    csv 格式，第一行为标题行，每行以英文逗号分隔，共三列：
    ➢ “OrderNo”表示订单编号，D0001、D0002、……、D0923。
    ➢ “ItemNo”表示货品编号，P0001、P0002、……、P1941。
    ➢ “Quantity”表示货品数量。
    以第一行数据为例，“D0001, P0128, 4”表示在订单 D0001 中，包括 4 件货品 P0128。

整体求解过程概述(摘要)

  针对问题一：本文首先处理附件一的信息，得到订单与货品种类的二值数矩阵，以批次中货品种类数量和被聚类的订单数为约束条件，以最小批次数量为目标函数的单目标规划模型，求解此模型的算法基于贪心思想，首先选择货品种类数最多的订单作为第一批次的聚类父点，为了表征第一批次的货品类别与未聚类的订单的货品类别的差异，本文建立了评价批次中的货品情况的聚合向量，以及未聚类订单的订单向量之间的向量差异评价算法，优先选择聚类后不新增货品总量的订单，然后选择差异度较少的订单，此时聚类向量的货品种类会开始增加，当货品种类增加到最大货架数的时候，此批次结束，然后从未聚类订单中再次选择最多货品种类的订单作为新批次的聚类父点，继续采用上述算法进行聚合，直到所有订单都被归入相应批次中。对此模型进行求解，最小批次数为 65，而每一批次的货品种类数量均接近给定的最大货架数200 个而不存在超出 200 个的情况。
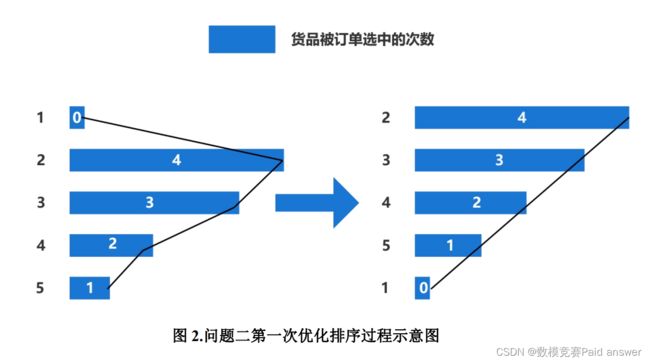
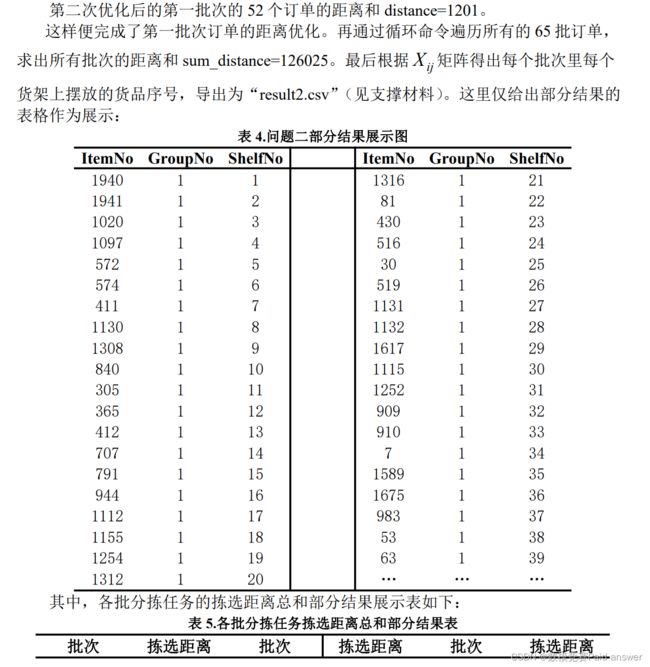
  针对问题二：本问要求在第一问的分批条件下，给出各批次中每一种货品的摆放位置，并且保证全部订单的拣选距离总和最小。本文以拣选距离总和最小为目标函数，建立了基于贪心算法和冒泡排序的货品摆放位置优化模型。先基于第一问的结果建立一个数据矩阵。首先进行第一次优化，采用贪心算法将被订单选中数量多的货品排到矩阵前端，从概率论上讲，这样能保证被订单高概率选到的货品相对集中地放置。再进行基于冒泡算法的二次优化。二次优化从上至下依次使得每个订单的距离最小，得出一个批次的拣选距离总和。最后得出各批分拣任务的拣选距离总和（见附录），以及所有批次全部订单的拣选距离总和为 126025。
  针对问题三：本问要求给出一个批次中的订单指派与分拣顺序策略的算法，使得一个批次中的每位分拣工的运动距离最小，以及五个分拣工最小运动距离的距离值尽可能均衡。本文根据这两个目标函数，建立了基于 0-1 指派问题的双目标规划模型。计算给定订单任务，求解最优订单顺序策略时，注意到其分拣的机理与图论中 TSP 模型较为相似，故本文对最小距离的求解采用遗传算法，考虑到分拣策略模型与传统TSP 模型的区别（即动态变化的距离矩阵），创新性地设置了二维决策变量来描述分拣行为，使得遗传算法更加匹配本文的策略模型。求解此模型即可满足分拣工的运动距离最小这一目标。本文发现指派矩阵可直接影响分拣工的运动距离均衡度，故本文提出了针对指派矩阵的自适应修正算法，以一个批次 5 个分拣工的运动距离的均方差作为均衡度的评价指标，通过不断修正指派矩阵使得均方差逐渐降低来满足距离值尽可能均衡的目标。最后得出满足双目标的最优指派与分拣策略。
  关键词：贪心算法；遗传算法；TSP 问题；0-1 指派；双目标非线性规划；自适应修正算法

问题分析：

  针对问题一，题目要求分批次数最少，据此判断目标函数为：求解最少的分批次数。基于贪心思想及目标函数，我们认为，想要分批次数最少，则需要尽量让每批的订单数更多；而每批的订单数越多，意味着该批的货品种类越多，问题一给出的约束条件为：每批次数最多为 200 类。
  因此，对于每一个订单，用一个 0-1 行矩阵来表征它的货品种类信息。基于贪心思想，优先考虑选取货品种类最多的一个订单作为“聚合父点”，因为该订单可以包括更多的子订单构成一个批次。将子订单与父订单进行聚合，得到为 0-1 形式的行矩阵。
  对于全部批次的订单，还可以确定另一个约束条件：任意订单矩阵都为全部聚合矩阵集合的子集。
  综上，基于贪心思想，根据聚合的思路，以上述两个约束条件作为限制，求解出最少批次数，并得到各批订单数量、货品种类数及分批具体方案。

  针对问题二，要求拣选距离总和最小，以此确定目标函数为求最小的拣选距离总和。基于贪心思想，将目标函数分化为逐步求局部最优解，最终期望通过不断缩小拣选距离总和得到整体最优解，局部最优策略的流程图如下：

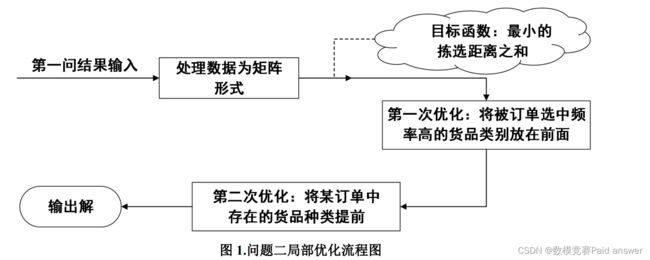
  首先，将附件 1 中的订单信息导入一个矩阵中，按照货品种类序号升序排列。此时可以得到按货品种类序号升序排列时的各类货品的拣选距离之和，这是优化前的拣选距离之和。
  进行第一步优化：基于贪心算法，对于多个订单的整体希望货品摆放的位置集中，设计一种优化排序方式：因为被订单选中次数多的类别的货品距离叠加次数多，所以需优先考虑将被订单选中次数多的商品类别放在前面顺序排列，以缩短距离总和，从而得到按被订单选中次数多少降序排列的货品序列。
  已知第一步优化的逻辑思路只是整体优化要求的必要条件，所以通过第一步优化不能得到整体最优结果；进一步思考，基于贪心思想，要使得距离和最小，即要让每一个订单的距离最小，此时可以将目标函数转化为求每一个订单的拣选距离最小。同时通过对数据的粗略观察可以看出，必然会存在大量被订单选中次数相等的货品种类。如果不经刻意排序，拣选距离和可能无法达到最小。
  基于以上思路进行第二次优化：将这些选中次数相等的货品类别及信息归于另一矩阵，仍然基于贪心算法的思想，欲使拣选距离总和最小，则局部目标函数为需要尽可能保证每一订单的拣选距离最小，即对于某个订单，需要将在该订单中存在的货品种类的排序提前。基于冒泡算法建立排序模型进行二次筛选，依次循环比较进行顺序调整，得到排序结果，并能够计算出拣选距离总和。
  进一步，将此算法应用于问题一的到的分批结果，分别得出各批拣选距离之和并得到全部批次的拣选距离总和。
  由于在利用贪心算法的贪心策略时，我们考虑的只是当下，这可能是现阶段最优的一种解决问题的方式，但我们却并不能保证其在最后的解题中是否是最优的一种解题方式[1]，所以，贪心算法很可能得到的是局部最优解而非整体最优解。最终，我们尝试用归纳法分析算法流程的逻辑以及条件的内在联系，并通过反证法重历上述流程，用理论分析粗略论证说明该算法得到的解为最优解。

  针对问题三，对于分拣工分拣订单的货品的具体情形，得到每一批次的的每一位分拣工的订单分拣顺序，要求每一位分拣工完成任务回到出发点后的运动总距离尽可能短，且分拣工之间的最短运动距离较为均衡。让每一位分拣工的订单任务由指定批次后生成的指派矩阵给出，每一位分拣工进行分拣订单的顺序决定了此分拣工的运动距离，故对于给定指派矩阵的 5 位分拣工建立了“其分拣订单的顺序”到“运动距离”的映射函数，并将此函数作为评价分拣工路线规划（分拣顺序）好坏的适应度函数。
  借助图论思想，类比旅行商问题对分拣工的分拣顺序给出决策变量并进行建模，使用遗传算法求解出每一位分拣工的最短运动路径，此时满足了“每一位分拣工完成任务回到出发点后的运动总距离尽可能短”这一要求；在得到五位分拣工各自的最短距离后，本文借助均方差来评价分拣工各自的最短距离的均衡度，为解决由于指派矩阵的随机性而导致的均衡度不佳，通过针对指派矩阵的自适应修正算法来使最短距离更加均衡，此算法满足了“分拣工之间的最短运动距离较为均衡”这一要求。

模型假设

  1. 假设根据贪心性质严格设计最优子问题求解，在无法继续设计出更进一步的最优子结构的时候，得到的结果无限接近整体最优解，可近似看作最优结果。
  2. 假设分拣工的运动路线不会发生冲突。
  3. 假设允许分拣工同时分拣同一货架上的货品。
  4. 假设只有一个订单的货品被全部分拣完成后，才能继续分拣下一个订单的货品。
  5. 假设分拣工的速度都为匀速且速度相同。
  6. 假设分拣过程中各种过程之间的转换和交际不耗费时间。
  7. 假设在处理某批次的订单过程中，分拣工经过一个货架，就完成对该货架对应的货品的分拣，不耗费时间且只需要经过一次。
  8. 假设一个拣货筐只用来装取一个订单中的货品，且拣货完成后自动转移至下一环节，仍然忽略拣货筐的生成、转换等各过程变化耗费的时间。
  9. 假设分拣时需遵循该批次的订单顺序，但不必考虑订单内不同类别的货品的处理顺序。
  10. 假设分拣工从 1 号货架出发，完成一个订单后可接着从到达位置继续前进，直到完成该批任务回到原点。
  11. 假设货架完全一致且均匀分布，间距为 1

模型的建立与求解：

  问题一：基于贪心思想求解最少订单分批次数的分批算法模型
  对于问题一要求的分批次数最少，确定目标函数：求解最少的分批次数。
  基于贪心思想，要求求解最少的分批次数，转换为使每批的订单数最多，近似于每批的货品种类最多，因此，选出货品种类数最多的订单与其它订单进行聚合，有利于在一个批次中囊括更多订单。
  通过聚合方法的设计，得到一个约束条件：任意订单矩阵都为全部聚合矩阵集合的子集。
  又根据题目条件给定的约束条件：每批产品的种类最多为 200 类。

问题一模型的准备与建立

问题一模型的求解：

  2. 首先归入不影响批次的总货品种类的订单：
  在第一批次已经具有一个货品种类数最多的订单条件下，首先遍历除已选订单外的其余订单，若发现存在一个暂不属于第一批次的订单，且其经过聚合判定为第 1 批次的子集时，直接将其归入第一批次。并且，由于聚合后未产生新的货品种类，故无需考虑货架数的增长。
  3. 对批次的总货品种类影响较小的订单优先被归入批次：
  在所有子集都归入第 1 批次后，接下来就是从聚合向量与订单向量的差异度最小的订单开始聚类，遍历计算所有还未聚类的订单的订单矩阵与聚合矩阵的差异度，选取差异度最小的进行聚类。聚类后，聚类矩阵出现新的货品种类分量，此时应该检测是否会聚合矩阵的货品总数超出货架数 N=200 的情况。若因为此订单的聚类而导致第一批次的总货品种类超出货架数，即：

  应拒绝此订单的该种聚合情况，此时第一批次的订单情况不再改变，聚类结束。
  Step3.循环以上步骤，建立新批次对订单进行归入聚类：
  1.新批次的建立：
  在还未归类的订单，选择种类数最大的订单作为批次 2 的第一个订单，更新批次 2的聚合向量，使用此聚合向量遍历剩下的未归类订单，判定其订单向量与聚合向量的差异度。
  2. 新批次的聚合：
  当差异度为 0，代表此订单是聚合向量的子集，其货品种类不会在归入批次后增加，故此类子集直接归入批次，且不考虑总货品种类不超过最大货架数；而对于具有差异度的订单，选择差异度最小的归入批次后，更新聚合向量，若此时聚合向量的货品种类数超过了货架数，则此批次的聚合结束。
  3.循环终止条件：

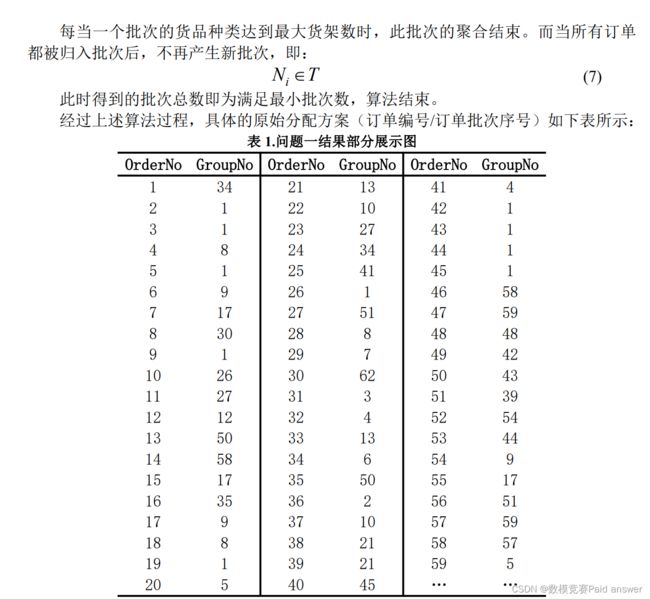
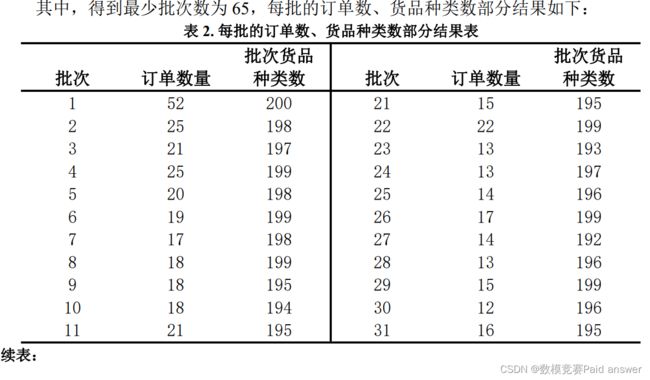
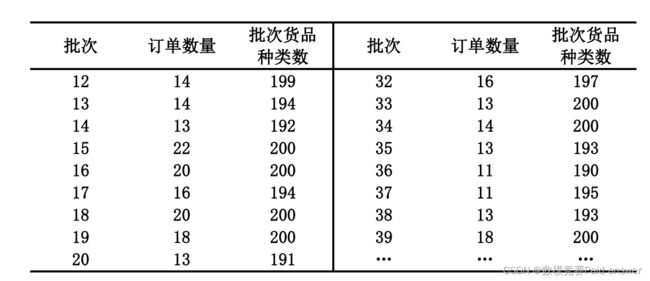
问题二模型的建立与求解：

  问题二：基于贪心思想和冒泡算法的货品摆放位置的优化模型

  要求对货品的摆放位置进行优化，使得同一批次中所有订单的拣选距离总和最小，
  根据此条件可以得到模型的目标函数为：对某一批次中所有订单求拣选距离之和，并求拣选距离之和的最小值。基于目标函数，结合贪心思想，对算法的流程进行优化，进行局部最优选择，结合问题二的分析，进行二次优化排序：
  Step1:第一步优化排序：
  对于某一批次的订单种类、货品种类类别、该类货品被订单选中的次数以及各类在各订单中的数量信息汇总，如下表：


  Step2:第二步优化排序：
  基于贪心思想，要使得距离和最小，在第一步的基础上，即要让每一个订单的距离最小，此时可以得到求局部最优结果的目标函数为：求每一个订单的拣选距离最小。
  则对于该批次中任意一个订单，需要将在该订单中存在的货品的排序提前，才能保证各订单的拣选距离最小。基于冒泡算法建立二次优化排序模型，依次循环比较进行顺序调整。






Step1:对排序优化模型的试算的检验：
  通过在第一问中对“附件 1.订单信息”进行处理得到可供编程利用的中间数据（见支撑材料“原始处理数据-订单与商品种类及数量”），利用题目的数据对上述排序优化模型的算法进行试算检验，（程序代码见支撑材料“Q2_shisuan.mlx”）观察它能否很好地将一个批次的拣选距离之和缩小。
  模拟一个批次的处理，我们中间数据（见支撑材料“原始处理数据-订单与商品种类及数量”）的前 220 行共计 11 个订单进行观察，假设其为一个批次。由于想要解决货架数为 200 的情况，基于贪心思想，仍然得到约束条件为：该批次货品类型不能超过 200 类。
  对原始数据建立规定排序的矩阵，并计算其拣选距离和为 12049。
  进行第一步优化，对原始矩阵重新排列。基于冒泡算法建立排序优化模型，首先如“模型的求解和建立”过程中的交换方法进行交换，对于 n 组数据，第一趟排序之后 a[n]的值一定是这组数据中最大的[3]，重复第 2 趟排序，直到完全满足条件，顺序不再调整。
  得到重新排序后的矩阵，并且我们能够计算其拣选距离之和减小到 1257。
  进行第二步优化，对每一组订单进行局部最优化排序，仍然根据“模型的求解和建立”过程中的交换方法采用冒泡排序算法进行交换，最终得到第二次优化排序后的矩阵，并计算其拣选距离之和减小到 771。
  综上可以发现通过优化局部优化进行二次排序，逐渐使得拣选距离总和缩小，且以上模型的局部优化流程在逻辑上可以证明为整体优化条件的充要条件，基本上可以判断该局部优化流程能够得到整体最优解。再结合假设中我们认为根据贪心性质严格设计最优子问题求解，在无法继续设计出更进一步的最优子结构的时候，得到的结果无限接近整体最优解，可近似看作最优结果。我们认为该结果即为最优结果。





  问题二贪心算法能够得到整体最优解的理论分析：
  Step1:对应用贪心算法的问题需满足的特点进行检验：
根据查阅资料得知，能够运用贪心算法求解的问题需要满足以下两个条件：
  1.贪心选择性质：所谓的贪心选择性质是指应用于同一规则，将问题变为一个相似的、但规模更小的子问题，而后每一步都是当前看似最佳的选择。
  2.局部最优解：运用贪心策略进行解题在每一次都取得了最优解。
  对于上述设计的算法流程，我们根据拣选距离总和的目标设计出一种排序策略，其中第一步优化排序可以看作求整体最优解的必要条件，而第二步优化排序在第一步优化排序的基础上进行，可以看作第一步优化排序的充分必要条件。而对于整体而言，该流程可以看作整体优化条件的充分必要条件，满足贪心选择性质。
  我们在第一步算法通过冒泡算法经过循环重复的顺序调整，得到的是局部最优解；同理，在第二部算法中同样运用冒泡算法得到了局部最优解。
  Step2:数学归纳法证明贪心算法得到整体最优解的可能性：
  通过整个流程，我们结合排序优化模型的试算结果进行分析，我们可以看到，原始阵列的距离和为 12049，第一次排序后的距离和为 1257，第二次排序后的距离和为771，距离和逐渐缩小，可以帮助我们从事实上判断第一步排序方法为“理论上存在的一种抽象最优排序方法”的必要条件，那么这种理论上的抽象排序方法为第一步排序的充分条件。
  对于第二步优化排序，我们设计它是在第一步排序的基础上，让每一组订单的距离都取最小值，那么距离总和即为最小，可以从逻辑上判定，第二步优化排序是在第一步优化排序的基础上实现目标的充分必要条件。
  在求解过程中，我们发现整体最优结果不止一种，而很可能是一个集合，我们的算法要求的是得到一组最优排序结果。那么，已知整体最优排序条件为第一步优化排序条件的充分条件，第二步优化排序条件为第一步优化排序条件的充分必要条件，根据充分条件与充分必要条件的包围关系，如下图所示：

  则可以确定，整个算法流程的抽象条件为求整体最优结果的充分必要条件，我们得到的这一组解必然为一组整体最优解。
  Step3:通过反证法进一步证明其为整体最优解的可能性：
  如果我们得到的解不是整体最优解，即我们的距离和还能继续减小，那么假设存在这么一组更小的距离和，逆推算法流程，第一步优化作为中间优化过程可以不必考虑，我们在第二步排序过程中，也必须满足第二步排序的条件，即一、二步流程都需要经历，那么说明，在第二步优化排序之后可能会存在一种进一步优化的条件，进行更多次优化。从逻辑上证明，第二次优化为在第一次优化基础上根据目标要求进行优化的充分必要条件，即不可能存在第三次优化的条件。所以上述假设不成立，那么得到的解在逻辑分析足够全面、没有忽略一些特殊情况的条件下，我们得到的解为整体最优解而非局部最优解。

论文缩略图：

程序代码：

clear
load item_01.mat item_mat
[a,b]=size(item_mat)
result=zeros(1,a);
P=1
flag=1
flagg=1
while ~isempty(find(result==0))
sigma_kind=[];%此列向量为每一笔订单的商品种类数
for i=1:
sigma_kind(i,1)=sum(item_mat(i,:));
if sigma_kind(i,1)==inf
sigma_kind(i,1)=0;
end
end
f=find(sigma_kind==max(sigma_kind),1);
father=item_mat(f,:);%最多种类的订单向量，将其作为聚类的父点
result(f)=P;
item_mat(find(sigma_kind==max(sigma_kind),1),:)=inf;%防止后续遍历时父点
被选择到
best_order=0;
flag=1; %%%%%%%
while flag==1
best_delta=inf;
for i=1:a
if item_mat(i,1)==inf
continue
end
DIFF=difference(father,item_mat(i,:));
if best_delta>DIFF
best_order=i;
best_delta=DIFF;
end
end
if best_delta==0
result(best_order)=P;
item_mat(best_order,:)=inf;
else
temp_father=father+item_mat(best_order,:);
temp_father(temp_father==2)=1;
if sum(temp_father)<=200
father=temp_father;
result(best_order)=P;
item_mat(best_order,:)=inf;
else
if
(sum(temp_father)>200)||(length(find(item_mat(:,1)==inf))==a)
sum_son(flagg,1)=(sum(father))
flagg=flagg+1;
flag=0;
end
end
end
end
P=P+1
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
find(result==65)
function delta=difference(father,son)%用于判断 father 向量与 son 向量的差
异度
together=father+son;
together(together==2)=1;
delta=norm(father-together);
end

获取论文及程序见最下方