Leetcode hot 100之双指针(快慢指针、滑动窗口)
目录
数组
有序的平方仍有序
删除/覆盖元素
移动零:交换slow和fast
滑动窗口:最短的连续子串(r++可行解->l--最短解)
最小长度的子数组
求和:sort、l = i + 1, r = len - 1
三数之和a+b+c=target
四数之和a+b+c+d=target
颜色分类(荷兰国旗):start=0、i、end=len-1
盛水最多:start=0、end=len-1 (水=哪边,则哪边往内走)
重复数:[1, n]
链表
相交点:长的链表先走len=long-short
倒数第n个:slow+1,fast+n
中点/回文/环:slow+1,fast+2
环入口:相遇点+1、头结点+1
归并排序
自底向上
自顶向下
双指针
数组
数组
有序的平方仍有序
删除/覆盖元素
if(nums[i] != val){
nums[k++] = nums[i]
}移动零:交换slow和fast
滑动窗口
初始化left = right = 0,把索引左闭右开区间[left, right)称为一个「窗口」。
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}最小覆盖子串
function minWindow(s, t) {
const need = new Map();
const window = new Map();
for (const c of t) {
need.set(c, (need.get(c) || 0) + 1);
}
let left = 0;
let right = 0;
let valid = 0;
let start = 0;
let len = Infinity;
while (right < s.length) {
const c = s[right];
right++;
if (need.has(c)) {
window.set(c, (window.get(c) || 0) + 1);
if (window.get(c) === need.get(c)) {
valid++;
}
}
while (valid === need.size) {
if (right - left < len) {
start = left;
len = right - left;
}
const d = s[left];
left++;
if (need.has(d)) {
if (window.get(d) === need.get(d)) {
valid--;
}
window.set(d, window.get(d) - 1);
}
}
}
return len === Infinity ? "" : s.substr(start, len);
}
字符串排列/异位词
function checkInclusion(t, s) {
const need = new Map();
const window = new Map();
for (const c of t) {
need.set(c, (need.get(c) || 0) + 1);
}
let left = 0;
let right = 0;
let valid = 0;
while (right < s.length) {
const c = s[right];
right++;
if (need.has(c)) {
window.set(c, (window.get(c) || 0) + 1);
if (window.get(c) === need.get(c)) {
valid++;
}
}
//与最小覆盖串的区别
while (right - left >= t.length) {
if (valid === need.size) {
return true;
}
//与最小覆盖串的区别
const d = s[left];
left++;
if (need.has(d)) {
if (window.get(d) === need.get(d)) {
valid--;
}
window.set(d, window.get(d) - 1);
}
}
}
return false;
}
最长无重复子串
function lengthOfLongestSubstring(s) {
const window = new Map();
let left = 0;
let right = 0;
let res = 0; // 记录结果
while (right < s.length) {
const c = s[right];
right++;
// 进行窗口内数据的一系列更新
window.set(c, (window.get(c) || 0) + 1);
// 判断左侧窗口是否要收缩
while (window.get(c) > 1) {
const d = s[left];
left++;
// 进行窗口内数据的一系列更新
window.set(d, window.get(d) - 1);
}
// 在这里更新答案
res = Math.max(res, right - left);
}
return res;
}
最小长度的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
类似于前缀和:区间求和
let ans = Infinity
while(end < len){
sum += nums[end];
while (sum >= target) {
ans = Math.min(ans, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}求和:sort、l = i + 1, r = len - 1
三数之和a+b+c=target
arr.sort()
let l = i + 1, r = len - 1, iNum = nums[i]
// 数组排过序,如果第一个数大于0直接返回res
if (iNum > 0) return res
// 去重
if (iNum == nums[i - 1]) continue
while(l < r) {
if (threeSum < 0) l++
else if (threeSum > 0) r--
else {
res.push([iNum, lNum, rNum])
// 去重
while(l < r && nums[l] == nums[l + 1]){
l++
}
while(l < r && nums[r] == nums[r - 1]) {
r--
}
l++
r--
}
}四数之和a+b+c+d=target
for(let i = 0; i < len - 3; i++) {
// 去重i
if(i > 0 && nums[i] === nums[i - 1]) continue;颜色分类(荷兰国旗):start=0、i、end=len-1
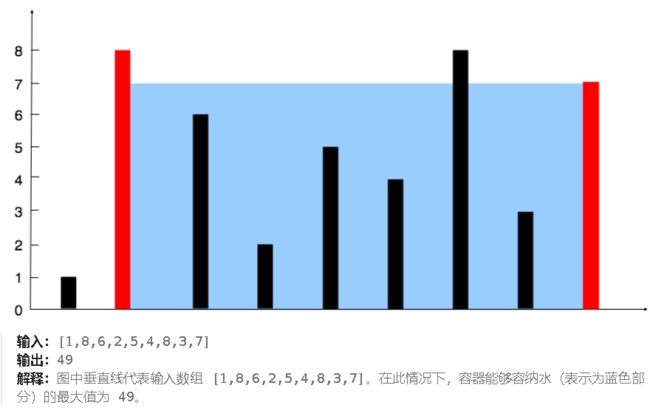
盛水最多:start=0、end=len-1 (水=哪边,则哪边往内走)
重复数:[1, n]
T(n):O(n)。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。
S(n):O(1)。只需要常数空间存放若干变量。
对 nums数组建图,每个位置 i连一条 i→nums[i] 的边。由于存在的重复的数字 target,因此 targe这个位置一定有起码两条指向它的边,因此整张图一定存在环,且我们要找到的 target就是这个环的入口
var findDuplicate = function(nums) {
let slow = 0, fast = 0;
do {
slow = nums[slow];
fast = nums[nums[fast]];
} while (slow != fast);
slow = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
};
链表
相交点:长的链表先走len=long-short
倒数第n个:slow+1,fast+n
中点/回文/环:slow+1,fast+2
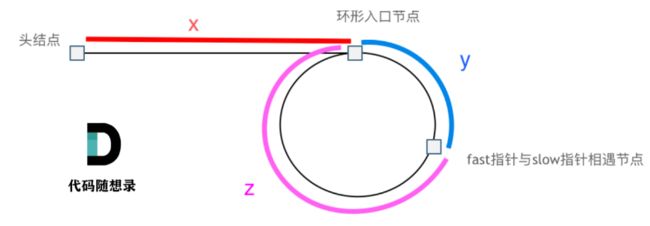
环入口:相遇点+1、头结点+1
相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A
(x + y) * 2 = x + y + n (y + z)
x = (n - 1) (y + z) + z
虽然实际中的n>1,当 n为1的时候,公式就化解为 x = z
从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。
归并排序
自底向上
T(n):O(nlogn)
S(n):O(1)
空间复杂度不是累计的,而是计算使用空间的峰值,
C/C++ 没有回收资源(new完后需要delete,不然内存泄漏照样是O(logn)),
但是像 java ,js这类语言会自动回收资源的
每次将链表拆分成若干个长度为 subLength 的子链表(最后一个子链表的长度可以小于 subLength)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val? 0 : val)
* this.next = (next? null : next)
* }
*/
const merge = (head1, head2) => {
let temp = new ListNode(0), temp1 = head1, temp2 = head2;
while (temp1&& temp2) {
if (temp1.val <= temp2.val) {
temp.next = temp1;
temp1 = temp1.next;
} else {
temp.next = temp2;
temp2 = temp2.next;
}
temp = temp.next;
}
if (temp1 !== null) {
temp.next = temp1;
} else if (temp2 !== null) {
temp.next = temp2;
}
return dummyHead.next;
}
var sortList = function(head) {
if (head === null) {
return head;
}
//获取长度
let length = 0;
let node = head;
while (node !== null) {
length++;
node = node.next;
}
const dummyHead = new ListNode(0, head);
for (let subLength = 1; subLength < length; subLength <<= 1) {
let prev = dummyHead, curr = dummyHead.next;
while (curr !== null) {
let head1 = curr;
for (let i = 1; i < subLength && curr.next; i++) {
curr = curr.next;
}
let head2 = curr.next;
curr.next = null;
curr = head2;
for (let i = 1; i < subLength && curr&& curr.next; i++)
curr = curr.next;
}
let next = null;
if (curr) {
next = curr.next;
curr.next = null;
}
const merged = merge(head1, head2);
//通过 prev 指针将已排序的子链表连接到一起
prev.next = merged;
while (prev.next) {
prev = prev.next;
}
//用 curr 指针继续遍历未排序的部分
curr = next;
}
}
return dummyHead.next;
};自顶向下
| 操作 |
内部排序 |
思想 |
稳定 |
平均 S(n) |
T(n) |
||
| 平均 |
最坏 |
最好 |
|||||
| 2-路归并 |
分治;分组排序,两两合并 相邻 有序序列 |
√ |
n |
nlog2n |
nlog2n逆序 |
nlog2n顺序 |
|
双指针
const merge = (head1, head2) => {
const dummyHead = new ListNode(0);
let temp = dummyHead, temp1 = head1, temp2 = head2;
while (temp1 !== null && temp2 !== null) {
if (temp1.val <= temp2.val) {
temp.next = temp1;
temp1 = temp1.next;
} else {
temp.next = temp2;
temp2 = temp2.next;
}
temp = temp.next;
}
if (temp1 !== null) {
temp.next = temp1;
} else if (temp2 !== null) {
temp.next = temp2;
}
return dummyHead.next;
}
const toSortList = (head, tail) => {
if (head === null) {
return head;
}
if (head.next === tail) {
head.next = null;
return head;
}
let slow = head, fast = head;
while (fast !== tail) {
slow = slow.next;
fast = fast.next;
if (fast !== tail) {
fast = fast.next;
}
}
const mid = slow;
return merge(toSortList(head, mid), toSortList(mid, tail));
}
var sortList = function(head) {
return toSortList(head, null);
};
数组
- key:
- left=arr.slice(0,mid)
- mergeLeft=mergeSort(left)
- res.push(leftArr.shift())
- res=res.concat(leftArr)
function mergesort(arr){
if(arr.length<2)return arr
let len=arr.length
let mid=parseInt(len/2)
let l1=arr.slice(0,mid)
let r1=arr.slice(mid,len)
let mergeleft=mergesort(l1)
let mergeright=mergesort(r1)
return merge(mergeleft,mergeright)
function merge(left,right){
let res=[]
while(left.length&&right.length){
if(left[0]<=right[0]){
res.push(left.shift())
}else{
res.push((right.shift()))
}
}
if(left.length){
res=res.concat(left)
}
if(right.length){
res=res.concat(right)
}
return res
}
}