pytorch_lesson3 张量的广播特性+逐点运算(基本运算+数值调整运算+数据科学运算)+规约运算+比较运算

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

提示：这里可以添加本文要记录的大概内容：

作为PyTorch中执行深度学习的基本数据类型，张量（Tensor）也拥有非常多的数学运算函数和方法，以及对应的一系列计算规则。在PyTorch中，能够作用与Tensor的运算，被统一称作为算子。并且相比于NumPy，PyTorch给出了更加规范的算子（运算）的分类，从而方便用户在不同场景下调用不同类型的算子（运算）。

---

提示：以下是本篇文章正文内容，下面案例可供参考

数学运算的分类
PyToch总共为Tensor设计了六大类数学运算，分别是：
1.逐点运算（Pointwise Ops）：指的是针对Tensor中每个元素执行的相同运算操作；
2.规约运算（Reduction Ops）：指的是对于某一张量进行操作得出某种总结值；
3.比较运算（Comparison Ops）：指的是对多个张量进行比较运算的相关方法；
4.谱运算（Spectral Ops）：指的是涉及信号处理傅里叶变化的操作；
5.BLAS和LAPACK运算：指的是基础线性代数程序集（Basic Linear Algeria Subprograms）和线性代数包（Linear Algeria Package）中定义的、主要用于线性代数科学计算的函数和方法；
6.其他运算（Other Ops）：其他未被归类的数学运算。

一、张量的广播（Broadcast）特性

示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。在具体介绍张量的运算操作之前，我们先要了解张量的运算规则，其中最重要的一点，就是张量具备和NumPy相同的广播特性，也就是允许不同形状的张量之间进行计算。

1.相同形状的张量计算

import torch
import numpy as np

t1 = torch.arange(3)
t1
#tensor([0, 1, 2])

t1+t1
#tensor([0, 2, 4])

相同形状数组总是可以进行广播计算。这里简单强调一下，虽然我们往往觉得不同形状之间的张量计算才是应用到广播特性，但其实相同形状的张量计算，尽管是对应位置元素进行计算，但本质上也是应用到了广播特性。

2.不同形状的张量计算

广播的特性是在不同形状的张量进行计算时，一个或多个张量通过隐式转化，转化成相同形状的两个张量，从而完成计算的特性。但并非任何两个不同形状的张量都可以通过广播特性进行计算，因此，我们需要了解广播的基本规则及其核心依据。

2.1 标量和任意形状的张量

标量可以和任意形状的张量进行计算，计算过程就是标量和张量的每一个元素进行计算。

t1 + 1
#tensor([1, 2, 3])
#一维维加零维
t1 + torch.tensor(1) 
#tensor([1, 2, 3])

##二维加零维
t2 = torch.zeros((3, 4))
t2
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])

t2+1
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])

2.2 相同维度、不同形状的张量之间计算

对于不同形状的张量计算，我们首先需要回顾张量的形状属性，并深化对其的理解。

t2.shape
#torch.Size([3, 4])

对于返回结果，我们可以看成是一个序列，代表着张量各维度的信息。当然，对于二维张量，由于我们可以将其视作一个矩阵，因此我们可以说t2是一个拥有三行四列的二维张量，但这种理解方式对于更高维度张量就存在一定的局限，因此我们需要树立另外一种理解方法，那就是：t2是由3个一维张量组成，并且该一维张量、每个都包含四个元素。类似的，我们可以创建更高维度张量并对其形状进行解释。

t3 = torch.zeros(3, 4, 5)
t3

tensor([[[0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.]],

        [[0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.]],

        [[0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.]]])

t3.shape
torch.Size([3, 4, 5])

我们可以将t3解释为：t3是3个二维张量组成了三维张量，并且这些每个二维张量，都是由四个包含五个元素的一维张量所组成。由二维拓展至三维，即可拓展至N维。

接下来，我们以t2为例，来探讨相同维度、不同形状的张量之间的广播规则。

t2 
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])

t2.shape
torch.Size([3, 4])

t21 = torch.ones(1, 4)
t21
#tensor([[1., 1., 1., 1.]])

t21的形状是（1， 4），和t2的形状（3， 4）在第一个分量上取值不同，但该分量上t21取值为1，因此可以广播，也就可以进行计算。

一般来说，广播指的是：至少有一个维度上的数值不同，有一个张量在这个维度上的值为1即可传播。

在上述的例子中，t21复制第一行的数值给第二、三行，然后每一行的每个数值都与t2进行相加

t2 + t21
'''
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
'''

实际的相加过程如下

t2 
'''
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])
'''

t22 = torch.ones(3, 1)
t22
'''
tensor([[1.],
        [1.],
        [1.]])
'''

t2 + t21
'''
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
'''

t2和t22有不同的列数，t22将第一列的数值复制给第二、三列，变换成和t2一样的形状，每个数值对应相加

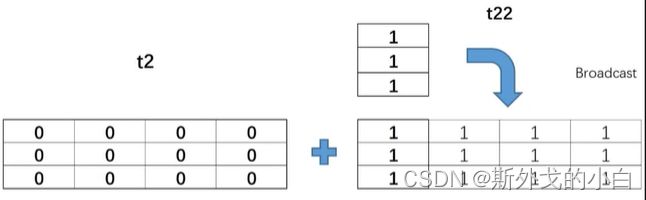
t23 = torch.ones(2, 4)
t23

tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.]])

t2
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])

t2 + t23

t2和t23在一个维度上的数值不同，但是因为两个张量在该维度上的值都不为1，所以没有办法进行广播并相加，所以会报错

t24 = torch.arange(3).reshape(3, 1)
t24

tensor([[0],
        [1],
        [2]])


t25 = torch.arange(3).reshape(1, 3)
t25
tensor([[0, 1, 2]])

t24 + t25
tensor([[0, 1, 2],
        [1, 2, 3],
        [2, 3, 4]])

此时，t24的形状是（3， 1），而t25的形状是（1， 3），二者的形状在两个份量上均不相同，但都有存在1的情况，因此也是可以广播的

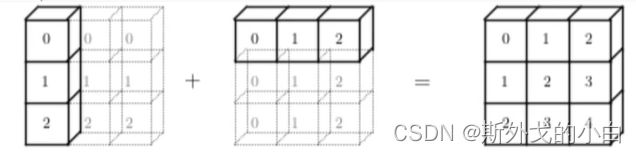
#三维张量的广播

t3 = torch.zeros(3, 4, 5)
t3
tensor([[[0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.]],

        [[0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.]],

        [[0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.],
         [0., 0., 0., 0., 0.]]])

t31 = torch.ones(3, 4, 1)
t31

tensor([[[1.],
         [1.],
         [1.],
         [1.]],

        [[1.],
         [1.],
         [1.],
         [1.]],

        [[1.],
         [1.],
         [1.],
         [1.]]])

t3 + t31
tensor([[[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]]])


t32 = torch.ones(3, 1, 5)
t32

tensor([[[1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.]]])


t32 + t3
tensor([[[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]]])

2.3 不同维度的张量计算过程中广播

在理解相同维度、不同形状的张量广播之后，对于不同维度的张量之间的广播其实就会容易很多，因为对于不同维度的张量，我们首先可以将低维的张量升维，然后依据相同维度不同形状的张量广播规则进行广播。而低维向量的升维也非常简单，只需将更高维度方向的形状填充为1即可，例如：

# 二维张量转化为三维张量
t2 = torch.arange(4).reshape(2, 2)
t2
tensor([[0, 1],
        [2, 3]])

# 转化为三维张量
t2.reshape(1, 2, 2)
tensor([[[0, 1],
         [2, 3]]])

t3 = torch.zeros(3, 2, 2)
t3
tensor([[[0., 0.],
         [0., 0.]],

        [[0., 0.],
         [0., 0.]],

        [[0., 0.],
         [0., 0.]]])

t2 + t3
tensor([[[0., 1.],
         [2., 3.]],

        [[0., 1.],
         [2., 3.]],

        [[0., 1.],
         [2., 3.]]])

t2在索引值为0的第一维度上升维，并且将第二维度上的数值三份，使得形状与t3一致，对应位置的数值相加即可

二、逐点运算（Pointwise Ops）

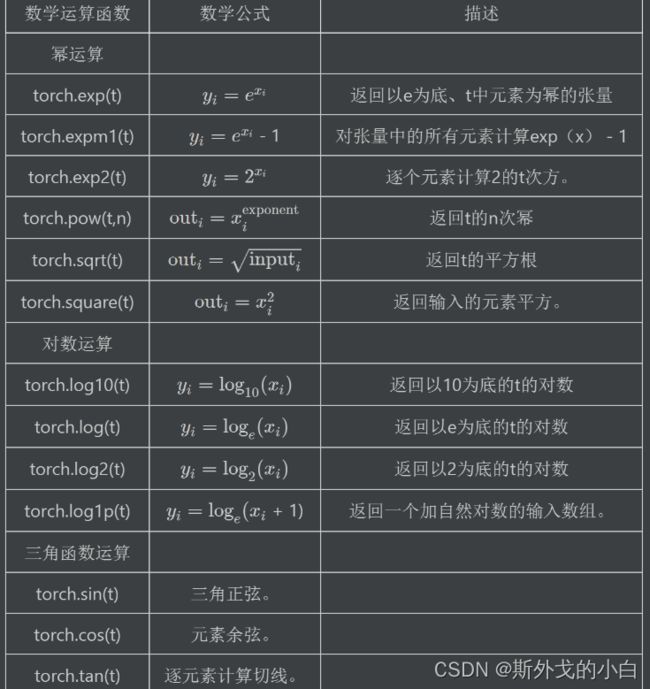
逐点运算主要包括数学基本运算、数值调整运算和数据科学运算三块，相关函数如下：

1.基本运算

t1 = torch.tensor([1, 2])
t1
tensor([1, 2])

t2 = torch.tensor([3, 4])
t2
tensor([3, 4])

torch.add(t1, t2)
tensor([4, 6])

t1 + t2
tensor([4, 6])

2.数值调整运算

torch.round(t)
tensor([0., -0., 0., 1., 2.])

torch.abs(t)
tensor([0.2684, 0.0247, 0.2931, 0.5017, 1.7832])

torch.neg(t)
tensor([-0.2684,  0.0247, -0.2931, -0.5017, -1.7832])

注：虽然此类型函数是数值调整函数，但并不会对原对象进行调整，而是输出新的结果。

t                # t本身并未发生变化

tensor([-0.5184, -0.4910, -0.1381, -0.2500, -0.4295])

而若要对原对象本身进行修改，则可考虑使用方法_()的表达形式，对对象本身进行修改。此时方法就是上述同名函数

t.abs_()
tensor([0.3783, 0.4897, 0.2027, 0.1249, 0.6198])

t
tensor([0.3783, 0.4897, 0.2027, 0.1249, 0.6198])

t.neg_()
tensor([-0.3783, -0.4897, -0.2027, -0.1249, -0.6198])

t
tensor([-0.3783, -0.4897, -0.2027, -0.1249, -0.6198])

除了上述数值调整函数有对应的同名方法外，本节介绍的许多科学计算都有同名方法。

3.数据科学运算

tensor的大多数科学计算只能作用于tensor对象

#计算2的2次方
torch.pow(2, 2)

报错的主要原因是我们需要对张量进行运算

torch.pow(torch.tensor(2), 2)
tensor(4)

理解：相比于Python原生数据类型，张量是一类更加特殊的对象，例如张量可以指定运行在CPU或者GPU上，因此很多张量的科学计算函数都不允许张量和Python原生的数值型对象混合使用。

tensor的大多数科学运算具有一定的静态性

所谓静态性，指的是对输入的张量类型有明确的要求，例如部分函数只能输入浮点型张量，而不能输入整型张量。

需要注意的是，虽然Python是动态编译的编程语言，但在PyTorch中，由于会涉及GPU计算，因此很多时候元素类型不会在实际执行函数计算时进行调整。此处科学运算大多数都要求对象类型是浮点型，我们需要提前进行类型转化。

t1 = torch.arange(1, 4).float()
t1
tensor([1., 2., 3.])

torch.exp(t1)
tensor([ 2.7183,  7.3891, 20.0855])

torch.expm1(t1)
tensor([ 1.7183,  6.3891, 19.0855])

注：expm1函数和log1p函数是一对对应的函数关系，后面再介绍log1p的时候会讲解这对函数的实际作用。

torch.square(t1)
tensor([1., 4., 9.])

torch.sqrt(t1) #2的t次方根
tensor([1.0000, 1.4142, 1.7321])

torch.pow(t1, 0.5) #开根号等同于0.5次方
tensor([1.0000, 1.4142, 1.7321])

torch.log10(t1)  #以10为底的t1的对数
tensor([0.0000, 0.3010, 0.4771])

torch.log2(t1) #以2为底的t1的对数
tensor([0.0000, 1.0000, 1.5850])

同时，我们也可简单回顾幂运算和对数运算之间的关系

torch.exp(torch.log(t1))  #先求以e为底的t1的对数q，然后再求以e为底的q次方，实际上得数还是原函数
tensor([1., 2., 3.])

torch.exp2(torch.log2(t1))
tensor([1., 2., 3.])

排序运算:sort

sort排序函数将同时返回排序结果和对应的索引值的排列

t = torch.tensor([1.0 , 3.0, 2.0])
t
tensor([1., 3., 2.])

#升序排列
torch.sort(t)
'''
torch.return_types.sort(
values=tensor([1., 2., 3.]),
indices=tensor([0, 2, 1]))
'''

#降序排列
torch.sort(t, descending=True)
'''
torch.return_types.sort(
values=tensor([3., 2., 1.]),
indices=tensor([1, 2, 0]))
'''

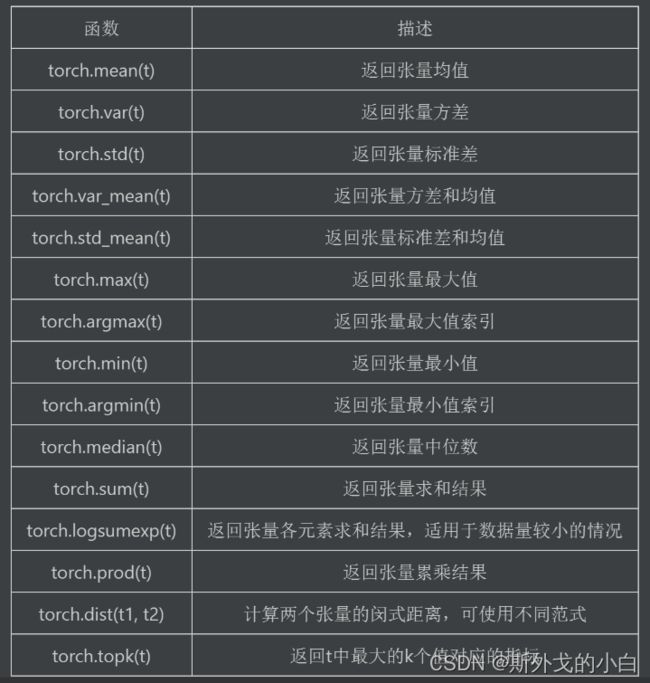
三、规约运算

规约运算指的是针对某张量进行某种总结，最后得出一个具体总结值的函数。此类函数主要包含了数据科学领域内的诸多统计分析函数，如均值、极值、方差、中位数函数等等。

#生成浮点型张量
t = torch.arange(10).float()
t
tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

#计算均值
torch.mean(t)
tensor(4.5000)

#计算标准差和均值
torch.std_mean(t)
(tensor(3.0277), tensor(4.5000))

#计算最大值
torch.max(t)
tensor(9.)

#返回最大值的索引
torch.argmax(t)
tensor(9)

#计算中位数
torch.median(t)
tensor(4.)

#求和
torch.sum(t)
tensor(45.)

#求积
torch.prod(t)
tensor(0.)

torch.prod(torch.tensor([1, 2, 3]))
tensor(6)

t3 = torch.arange(24).float().reshape(2, 3, 4)
t3
tensor([[[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.]],

        [[12., 13., 14., 15.],
         [16., 17., 18., 19.],
         [20., 21., 22., 23.]]])

t3.shape
torch.Size([2, 3, 4])

torch.sum(t3, dim=0) #按照最外层的维度将行相加，即将两个二维张量的行分别相加
tensor([[12., 14., 16., 18.],
        [20., 22., 24., 26.],
        [28., 30., 32., 34.]])

torch.sum(t3, dim=1)  #从外到里的第二个维度上进行相加，即两个二维向量，分别将每行想相加
tensor([[12., 15., 18., 21.],
        [48., 51., 54., 57.]])

torch.sum(t3, dim=2)  #从外到里第三个维度上进行相加，即两个二维向量分别将列进行相加
torch.sum(t3, dim=2)  #从外到里第三个维度上进行相加，即两个二维向量分别将列进行相加
torch.sum(t3, dim=2)  #从外到里第三个维度上进行相加，即两个二维向量分别将列进行相加
tensor([[ 6., 22., 38.],
        [54., 70., 86.]])

dist计算距离
dist函数可以计算闵可夫斯基距离，通过输入不同的p值，可以计算多种类型的距离，例如欧式距离、街道距离，闵可夫斯基距离公式如下：

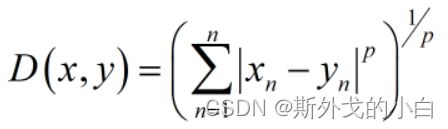
t1 = torch.tensor([1.0, 2])
t1
tensor([1., 2.])

t2 = torch.tensor([3.0, 4])
t2
tensor([3., 4.])

torch.dist(t1, t2, 2) #令p等于2计算欧式距离
tensor(2.8284)

torch.sqrt(torch.tensor(8.0))
tensor(2.8284)

#当p取值为1时，计算街道距离
torch.dist(t1, t2, 1)
tensor(4.)

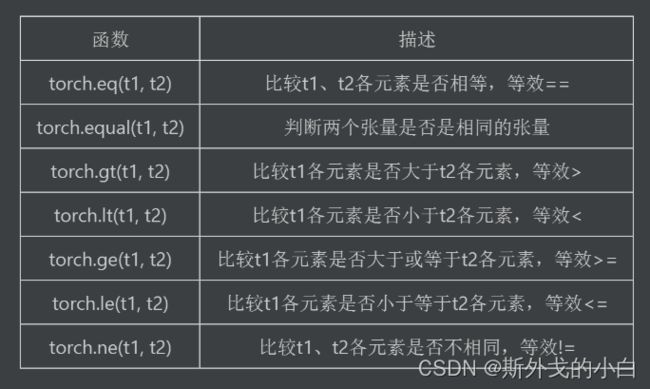
四、比较运算

t1 = torch.tensor([1.0, 3, 4])
t2 = torch.tensor([1.0, 2, 5])
t1 == t2
tensor([ True, False, False])

t1 > t2
tensor([False,  True, False])

torch.gt(t1, t2)
tensor([False,  True, False])

t1 >= t2
tensor([ True,  True, False])

torch.ge(t1, t2)
tensor([ True,  True, False])