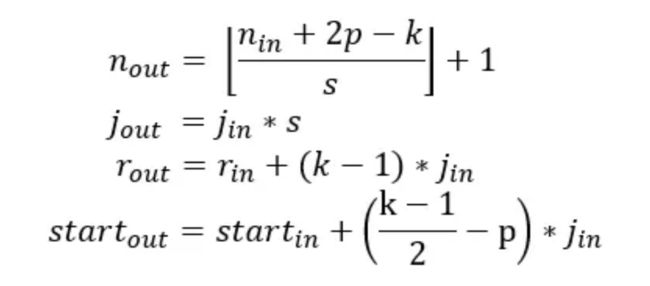容易被忽视的CNN模型的感受野及其计算
感受野可能是卷积神经网络中最重要的概念之一,在学术中也被广泛关注。几乎所有的目标检测方法都围绕感受野来设计其模型结构。这篇文章通过可视化的方法来表达感受野的信息,并且提供一用于计算任何CNN网络每一层感受野的程序。
对于CNN相关的基础知识,可以参考A guide to convolution arithmetic for deep learning。
首先看一下感受野的定义,感受野是指在输入特征图上影响某一个特定的特征层上某一个具体的特征的区域。一个特征的感受野可以用其中心位置和尺寸来描述。如下图1所示,
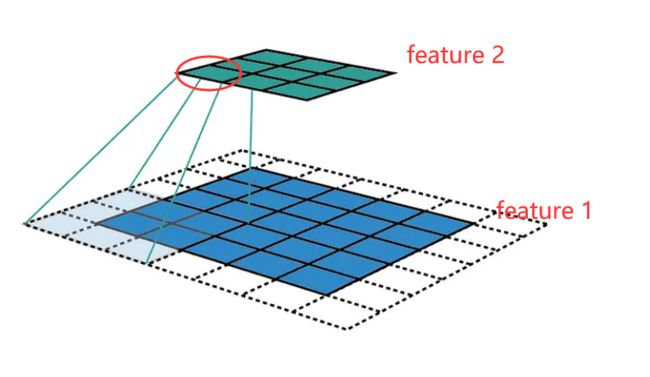
在feature 2上圆圈圈出的特征,对应到feature 1上是一块3x3的区域影响此特征,所以feature 2 layer的感受野大小是3。
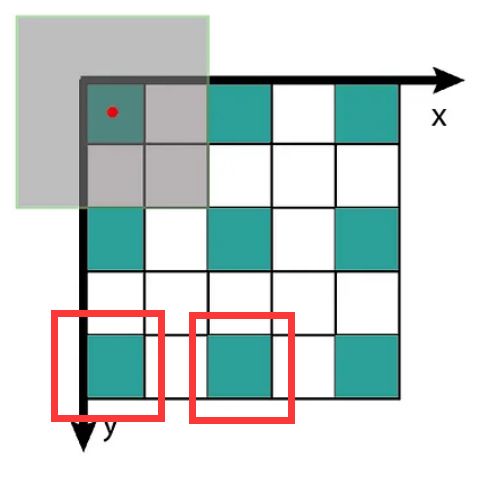
下图2描述了一个感受野的例子。我们使用 5 ∗ 5 5*5 5∗5的输入特征图,卷积核大小 k = 3 ∗ 3 k=3*3 k=3∗3,padding p = 1 p=1 p=1,stride s = 2 ∗ 2 s = 2*2 s=2∗2的卷积核。根据A guide to convolution arithmetic for deep learning中提供的公式计算得到输出特征图的尺寸为3x3。然后继续在此特征图上使用相同的卷积核执行卷积操作,得到2x2的特征图。
其中,
i i i:输入特征图的尺寸
p p p:padding size
k k k:kernel size
s s s:stride size
下图3左侧的图展示的是常规的CNN不同特征图之间的展示方法,但是这种方法比较难以看出感受野的中心坐标,也比较难看出感受野的大小。上图右侧的图每个feature map使用了与input相同的大小来表示,然后经过卷积后的特征图使用稀疏的表示方式来表达。这种表达方式可以清楚的看到感受野的中心位置和感受野的大小。例如上图右侧图中,绿色的特征图上的特征点的感受野大小是3,黄色特征图的感受野大小为6.
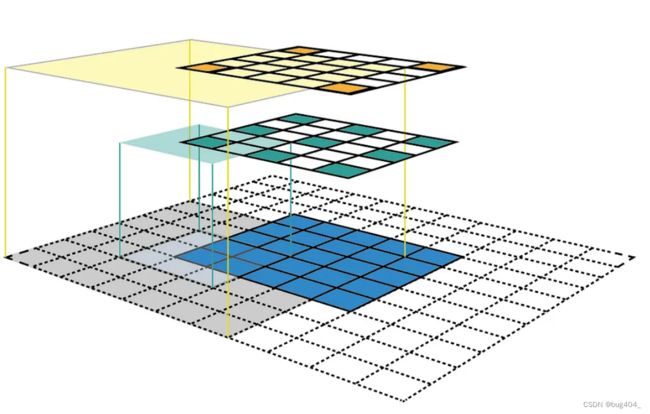
下图4所示是另一个感受野的例子,这个使用了更大的输入特征图,9x9的特征图。下图作图是3D的表示,右图是2D的表示法。我们可以看到,在第二个特征图上的特征,其感受野大小为7x7,几乎覆盖了整个输入特征图的大小。感受野越大,对于深层的CNN网络的性能越好,因此这也是网络设计需要考虑的因素。
感受野尺寸的计算公式
上面式子中,
-
第一个公式计算的是每层输出特征图的尺寸,其中, n i n n_{in} nin表示输入特征图的尺寸, p p p表示padding size, k k k表示kernel size, s s s表示stride, n o u t n_{out} nout表示输出特征图的尺寸。
-
第二个公式计算的是使用图2右侧的特征图表示法时,特征图上每个特征之间的jump。其等于输入特征图的jump j i n j_{in} jin乘以 s s s stride。例如下图的特征图中,每两个特征之间的jump是2.
- 第三个公式计算的是当前输出特征图的特征所对应的感受野大小。其中, r i n r_{in} rin表示输入特征图所属特征的感受野大小, k k k表示kernel size, j i n j_{in} jin表示输入特征图每两个特征之间的jump。如下图所示,在图中,绿色特征图的 r i n = 3 , k = 3 , j i n = 2 r_{in}=3,k=3,j_{in}=2 rin=3,k=3,jin=2,所以黄色特征图的感受野大小为 r o u t = r i n + ( k − 1 ) ∗ j i n = 3 + 2 ∗ 2 = 7 r_{out} = r_{in} + (k-1)*j_{in} = 3 + 2 * 2 = 7 rout=rin+(k−1)∗jin=3+2∗2=7,与我们图上直观看到的结论一致。
- 第四个公式计算的是感受野的中心点坐标。
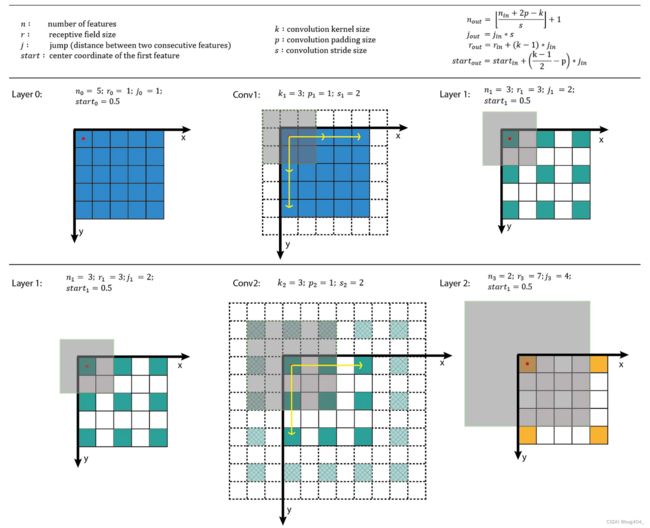
下面我们用一个直观的例子来计算下整个过程。对于第一个输入特征图,总是有 n = i m a g e s i z e , r = 1 , j = 1 , s t a r t = 0.5 n = image size, r = 1, j = 1, start = 0.5 n=imagesize,r=1,j=1,start=0.5。在下图中,输入特征图的中心点在图上坐标轴的坐标为0.5。
经过最后的计算,得到最后特征图的感受野大小为7。下面我们通过程序来验证一下。
# [filter size, stride, padding]
#Assume the two dimensions are the same
#Each kernel requires the following parameters:
# - k_i: kernel size
# - s_i: stride
# - p_i: padding (if padding is uneven, right padding will higher than left padding; "SAME" option in tensorflow)
#
#Each layer i requires the following parameters to be fully represented:
# - n_i: number of feature (data layer has n_1 = imagesize )
# - j_i: distance (projected to image pixel distance) between center of two adjacent features
# - r_i: receptive field of a feature in layer i
# - start_i: position of the first feature's receptive field in layer i (idx start from 0, negative means the center fall into padding)
import math
# 定义这个example的两层网络的参数,kernel size = 3, stride = 2, padding = 1
convnet = [[3,2,1],[3,2,1]]
layer_names = ['conv1','conv2']
# 定义输入特征图的尺寸
imsize = 5
def outFromIn(conv, layerIn):
n_in = layerIn[0]
j_in = layerIn[1]
r_in = layerIn[2]
start_in = layerIn[3]
k = conv[0]
s = conv[1]
p = conv[2]
n_out = math.floor((n_in - k + 2*p)/s) + 1
actualP = (n_out-1)*s - n_in + k
pR = math.ceil(actualP/2)
pL = math.floor(actualP/2)
j_out = j_in * s
r_out = r_in + (k - 1)*j_in
start_out = start_in + ((k-1)/2 - pL)*j_in
return n_out, j_out, r_out, start_out
def printLayer(layer, layer_name):
print(layer_name + ":")
print("\t n features: %s \n \t jump: %s \n \t receptive size: %s \t start: %s " % (layer[0], layer[1], layer[2], layer[3]))
layerInfos = []
if __name__ == '__main__':
#first layer is the data layer (image) with n_0 = image size; j_0 = 1; r_0 = 1; and start_0 = 0.5
print ("-------Net summary------")
currentLayer = [imsize, 1, 1, 0.5]
printLayer(currentLayer, "input image")
for i in range(len(convnet)):
currentLayer = outFromIn(convnet[i], currentLayer)
layerInfos.append(currentLayer)
printLayer(currentLayer, layer_names[i])
print ("------------------------")
layer_name = input ("Layer name where the feature in: ")
layer_idx = layer_names.index(layer_name)
idx_x = int(input ("index of the feature in x dimension (from 0)"))
idx_y = int(input ("index of the feature in y dimension (from 0)"))
n = layerInfos[layer_idx][0]
j = layerInfos[layer_idx][1]
r = layerInfos[layer_idx][2]
start = layerInfos[layer_idx][3]
assert(idx_x < n)
assert(idx_y < n)
print ("receptive field: (%s, %s)" % (r, r))
print ("center: (%s, %s)" % (start+idx_x*j, start+idx_y*j))
执行其输出为
-------Net summary------
input image:
n features: 5
jump: 1
receptive size: 1 start: 0.5
conv1:
n features: 3
jump: 2
receptive size: 3 start: 0.5
conv2:
n features: 2
jump: 4
receptive size: 7 start: 0.5
------------------------
Layer name where the feature in: conv2
index of the feature in x dimension (from 0)0
index of the feature in y dimension (from 0)0
receptive field: (7, 7)
center: (0.5, 0.5)