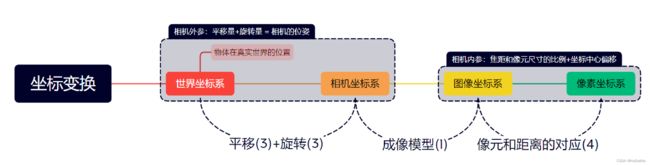
相机成像坐标系转换的运算过程
前言
相机系统可以把现实世界中的三维点对应到成像平面系统上的二维点,通常的体系描述下,这个过程涉及到四个坐标系和三次变化。本文单纯地详细的介绍下计算的过程和结果,会有一些概念上的延申,不涉及相机标定的详细说明,也不涉及畸变介绍,可作为图形学的基础知识浏览。
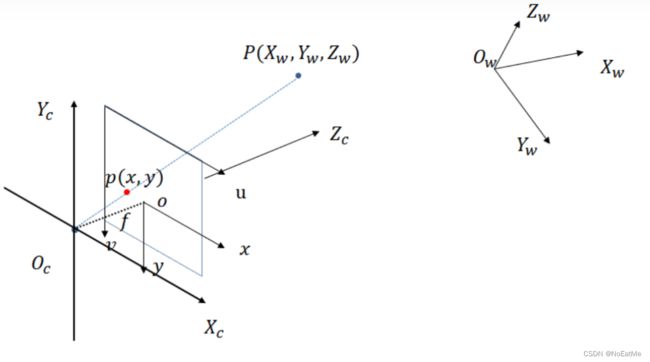
四个坐标系
-
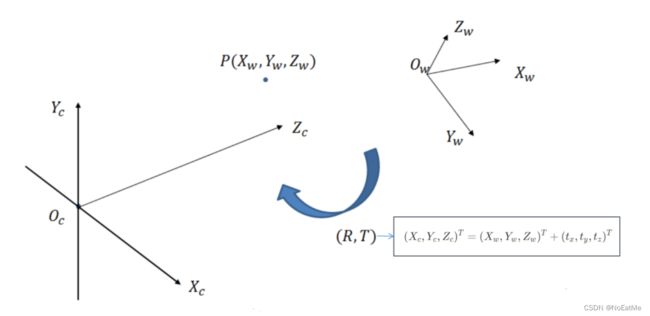
世界坐标系:记录点在真实世界中的具体位置,是一个三维坐标。坐标系的安放方式原则上随意随意,但实际上会为了减少计算量做一些特殊安排(比如相机标定中放在标靶的左上角)。图中及此文中记为 ( X w , Y w , Z w ) (X_w,Y_w,Z_w) (Xw,Yw,Zw)
-
相机坐标系:简单来说是从相机的角度来观察现实世界中的位置信息,基于这一点,相机坐标系的安放不再那么随意,需要满足
- 相机坐标系的一个轴(通常为 Z Z Z轴和相机的光轴重合)
- 坐标系的原点 O c O_c Oc位于相机的光心
相机坐标系仍然是三维坐标,这点显然,图中及此文中记为 ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc)
-
图像坐标系:图像坐标系可以理解为我们实际的成像平面(探测器平面)重合的二维坐标系,他的尺度是距离尺度,之所以要强调这一点,是为了和后面的像素坐标系做区分。另外,成像平面的坐标系一般原则上会:
- 把原点 o o o放在光轴上(与 Z c Z_c Zc重合)
- x y xy xy坐标轴和相机坐标系对应平行
图中及此文中记为 ( x , y ) (x,y) (x,y)
-
像素坐标系:基本和图像坐标系的实际含义相同知识尺度是像素的尺度,也就是离散的像素做坐标。通常情况下此文中记为 ( u , v ) (u,v) (u,v)
总结如下:
| 名称 | 坐标 | 维度 | 含义 |
|---|---|---|---|
| 世界坐标系 | ( X w , Y w , Z w ) (X_w,Y_w,Z_w) (Xw,Yw,Zw) | 3 | 物体在真实世界中的坐标 |
| 相机坐标系 | ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc) | 3 | 在相机视角下的物体坐标 |
| 图像坐标系 | ( x , y ) (x,y) (x,y) | 2 | 成像平面上的距离尺度坐标 |
| 像素坐标系 | ( u , v ) (u,v) (u,v) | 2 | 成像平面上的像素尺度坐标 |
三次变换
- 世界坐标系->相机坐标系:作为三维坐标系之间的变换,实际上是完全基于坐标转换的数学变换,变换前后都是三维坐标,只不过观测基准变了
- 相机坐标系->图像坐标系:三维转换为二维的关键一步,结合高斯成像公式,具有切实的物理意义
- 图像坐标系->像素坐标系:单纯的尺度转换,非常的简单
世界坐标系->相机坐标系
平移
( X c , Y c , Z c ) T = ( X w , Y w , Z w ) T + ( t x , t y , t z ) T (X_c,Y_c,Z_c)^T = (X_w,Y_w,Z_w)^T + (t_x,t_y,t_z)^T (Xc,Yc,Zc)T=(Xw,Yw,Zw)T+(tx,ty,tz)T
旋转
旋转的影响主要涉及三个转动角度,我们先只考虑绕 Z Z Z轴旋转的情况:对于点 ( X w , Y w , Z w ) (X_w,Y_w,Z_w) (Xw,Yw,Zw)
,将其绕相机坐标系下的 Z Z Z轴旋转 θ \theta θ,求新点坐标。
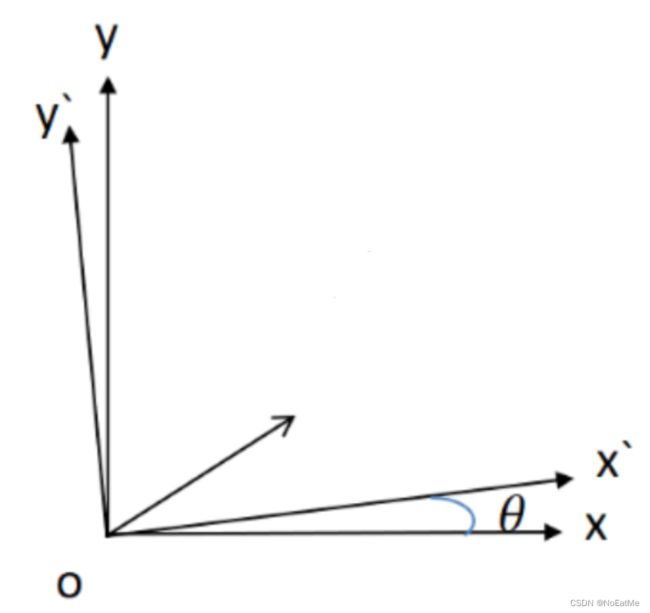
我们先把向量 ( X w , Y w ) (X_w,Y_w) (Xw,Yw)分解到对应坐标轴上,变成 ( X w , 0 ) (X_w,0) (Xw,0)和 ( 0 , Y w ) (0,Y_w) (0,Yw)
旋转 θ \theta θ之后:
( X w , 0 ) = > ( X w c o s θ , X w s i n θ ) ( 0 , Y w ) = > ( − Y w s i n θ , Y w c o s θ ) (X_w,0) =>(X_wcos\theta ,X_wsin\theta)\\ (0,Y_w) =>(-Y_wsin\theta ,Y_wcos\theta) (Xw,0)=>(Xwcosθ,Xwsinθ)(0,Yw)=>(−Ywsinθ,Ywcosθ)
则有:
[ X c Y c ] = [ c o s θ z − s i n θ z s i n θ z y c o s θ z ] ⋅ [ X w Y w ] \begin{bmatrix} X_c\\ Y_c\\ \end{bmatrix}= \begin{bmatrix} cos\theta_z & -sin\theta_z \\ sin\theta_z & ycos\theta_z \\ \end{bmatrix} \cdot \begin{bmatrix} X_w\\ Y_w\\ \end{bmatrix} [XcYc]=[cosθzsinθz−sinθzycosθz]⋅[XwYw]
补齐 Z Z Z维度:
[ X c Y c Z c ] = [ c o s θ z − s i n θ z 0 s i n θ z y c o s θ z 0 0 0 1 ] ⋅ [ W w Y w Z w ] \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}= \begin{bmatrix} cos\theta_z & -sin\theta_z & 0\\ sin\theta_z & ycos\theta_z & 0\\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} W_w\\ Y_w\\ Z_w \end{bmatrix} XcYcZc = cosθzsinθz0−sinθzycosθz0001 ⋅ WwYwZw
我们将 Z Z Z方向上的旋转矩阵记为 r z r_z rz,并略过其他两个方向的雷同计算,有:
r x = [ 1 0 0 0 c o s θ x − s i n θ x 0 s i n θ x c o s θ x ] r y = [ c o s θ y 0 s i n θ y 0 1 0 − s i n θ y 0 c o s θ y ] r z = [ c o s θ z − s i n θ z 0 s i n θ z y c o s θ z 0 0 0 1 ] r_x =\begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta_x & -sin\theta_x\\ 0 & sin\theta_x & cos\theta_x \end{bmatrix} \\ r_y = \begin{bmatrix} cos\theta_y & 0 & sin\theta_y\\ 0 & 1 & 0\\ -sin\theta_y & 0 & cos\theta_y \end{bmatrix} \\ r_z = \begin{bmatrix} cos\theta_z & -sin\theta_z & 0\\ sin\theta_z & ycos\theta_z & 0\\ 0 & 0 & 1 \end{bmatrix} rx= 1000cosθxsinθx0−sinθxcosθx ry= cosθy0−sinθy010sinθy0cosθy rz= cosθzsinθz0−sinθzycosθz0001
然后将三个分量的旋转量相乘可以得到最后的结果,由于式子非常复杂,我们写成这样的形式:
R = r x ⋅ r y ⋅ r z = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] R = r_x \cdot r_y \cdot r_z =\begin{bmatrix}r_{11} & r_{12} & r_{13}\\r_{21} & r_{22} & r_{23}\\r_{31} & r_{32} & r_{33}\\\end{bmatrix} R=rx⋅ry⋅rz= r11r21r31r12r22r32r13r23r33
其实这个旋转矩阵还是非常特殊的矩阵,拥有很好的性质(正交+单元),以后有机会介绍相机标定的时候会详细说明。
整理
( X c Y c Z c ) = R ⋅ ( X w Y w Z w ) + t = ( r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ) ( X w Y w Z w ) + ( t x t y t z ) \begin{pmatrix}X_c\\Y_c\\Z_c\end{pmatrix}=R\cdot \begin{pmatrix}X_w\\Y_w\\Z_w\end{pmatrix}+ t =\begin{pmatrix}r_{11} & r_{12} & r_{13} \\r_{21} & r_{22} & r_{23} \\r_{31} & r_{32} & r_{33} \\\end{pmatrix}\begin{pmatrix}X_w\\Y_w\\Z_w\end{pmatrix}+\begin{pmatrix}t_x\\t_y\\t_z\end{pmatrix} XcYcZc =R⋅ XwYwZw +t= r11r21r31r12r22r32r13r23r33 XwYwZw + txtytz
展开并补齐次:
( X c Y c Z c 1 ) = ( r 11 r 12 r 13 t x r 21 r 22 r 23 t y r 31 r 32 r 33 t z 0 0 0 1 ) ( X w Y w Z w 1 ) = ( R 3 × 3 t 3 × 1 0 1 ) ( X w Y w Z w 1 ) \begin{pmatrix}X_c\\Y_c\\Z_c\\1\end{pmatrix}=\begin{pmatrix}r_{11} & r_{12} & r_{13} & t_x\\r_{21} & r_{22} & r_{23} & t_y\\r_{31} & r_{32} & r_{33} & t_z\\0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix}X_w\\Y_w\\Z_w\\1\end{pmatrix}=\begin{pmatrix}R_{3\times 3} & t_{3\times1}\\0 & 1\end{pmatrix}\begin{pmatrix}X_w\\Y_w\\Z_w\\1\end{pmatrix} XcYcZc1 = r11r21r310r12r22r320r13r23r330txtytz1 XwYwZw1 =(R3×30t3×11) XwYwZw1
在相机标定中,我们常常把旋转矩阵和平移矩阵(共计6个自由度)称之为相机的外参
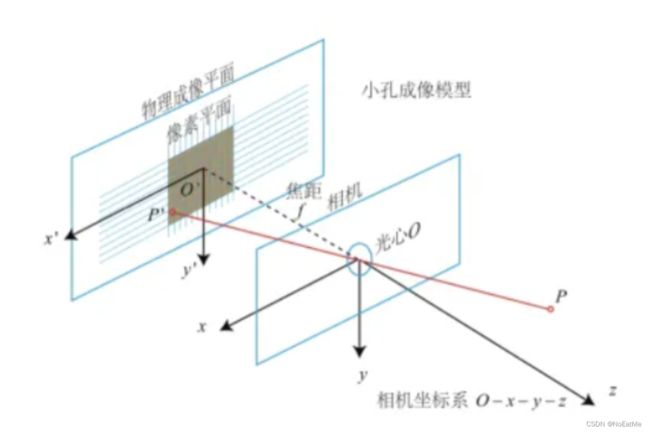
相机坐标系->图像坐标系
这一步是基于相机的成像系统,如下图所示
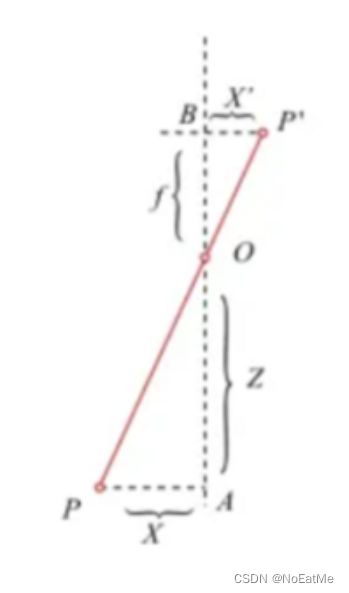
为了方便观察,有此图:
根据相似三角形:
Z c f = X c x = Y c y \frac{Z_c}{f} = \frac{X_c}{x} = \frac{Y_c}{y} fZc=xXc=yYc
也就是:
x = f X c Z c y = f Y c Z c x = f\frac{X_c}{Z_c}\\ y = f\frac{Y_c}{Z_c} x=fZcXcy=fZcYc
用矩阵表示:
[ x y 1 ] = 1 Z c [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] \begin{bmatrix}\ x\\y\\1 \end{bmatrix} =\frac{1}{Z_c} \begin{bmatrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} X_c\\Y_c\\Z_c\\1 \end{bmatrix} xy1 =Zc1 f000f0001000 XcYcZc1
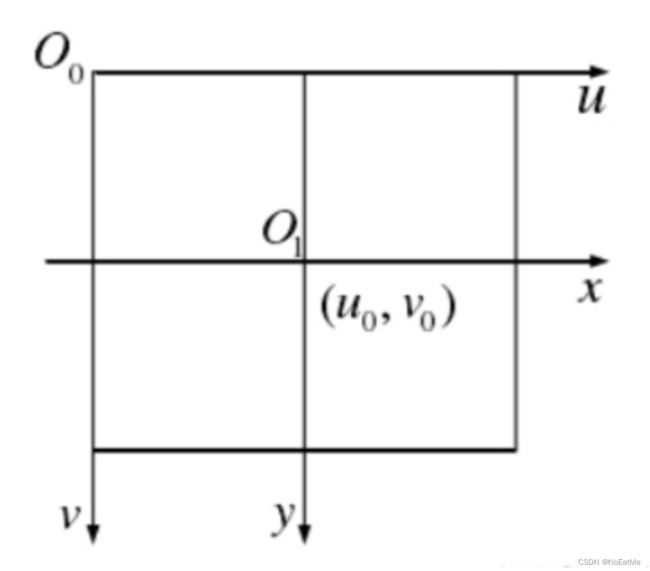
图像坐标系->像素坐标系
这一步是单纯的尺度变换,图中 O 1 O_1 O1是图像坐标系的坐标原点,也是相机光心所在地。 O o O_o Oo
是像素坐标系原点, ( u 0 , v 0 ) (u_0,v_0) (u0,v0)是两个坐标系原点的偏移量
假设每个像素的宽度和长度是 d x , d y dx,dy dx,dy
p ( u , v ) = p ( x d x + u 0 , y d y + v 0 ) p(u,v) = p(\frac{x}{dx} + u_0,\frac{y}{dy}+v_0) p(u,v)=p(dxx+u0,dyy+v0)
考虑矩阵的写法:
[ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x y 1 ] (2) \begin{bmatrix}\tag2 u\\v\\1 \end{bmatrix}= \begin{bmatrix} \frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix} uv1 = dx1000dy10u0v01 xy1 (2)
另: f d x \frac{f}{dx} dxf常常被写成 f x f_x fx, f d y \frac{f}{dy} dyf常常被写成 f y f_y fy
结果整理:
[ u v 1 ] = 1 Z c [ f x 0 u 0 0 0 f y v 0 0 0 0 1 0 ] ( r 1 r 2 r 3 t x r 4 r 5 r 6 t y r 7 r 8 r 9 t z 0 0 0 1 ) [ X w Y w Z w 1 ] \begin{bmatrix} u\\v\\1 \end{bmatrix}= \frac{1}{Z_c} \begin{bmatrix} f_x & 0 & u_0 & 0\\ 0 & f_y & v_0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{pmatrix} r_1 & r_2 & r_3 & t_x\\ r_4 & r_5 & r_6 & t_y\\ r_7 & r_8 & r_9 & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{bmatrix} X_w\\Y_w\\Z_w\\1 \end{bmatrix} uv1 =Zc1 fx000fy0u0v01000 r1r4r70r2r5r80r3r6r90txtytz1 XwYwZw1
至此,从世界坐标系到像素坐标系的转换完成