9.28栈、队列&状态压缩&双向搜索

栈、队列

有效括号

可能左括号多，右括号少

可能第一个出现的右括号和最后一个左括号不匹配

可能没遇到左括号就遇到了右括号

有效括号过程中最大栈长度

遇到左括号，就在入栈期望遇到的对应右括号，并比较当前栈长度和最大长度，更新；

遇到右括号，和栈顶元素判定一下，匹配的话就出栈并消掉，让栈长度--，不然就接着往后，什么也不做（实际上已经是非法括号序列了）

滑动窗口最大值

首先考虑窗口长度是否大于数组长度

然后思路是确定窗口尾部的坐标（右），然后根据窗口长度确定窗口头的坐标

队列中元素：遇到元素时，应先判别队列头的元素是否还合法，直到遇到合法的队头或全部清空

合法的队头就意味着当前的窗口的最大值

接着比较合法的窗口和当前元素，如果当前元素大于，就删掉这个元素（队尾）之前所有小于它的元素，直到遇到不小于它的

如果当前元素小于，就入队列，因为之前元素会比现在先出队列，当前元素依然可以当最大值

用双端队列就是因为队头可以出元素

状态压缩

将一个状态压缩为一个整数（通常为二进制数），就可以在更为方便地进行状态转移的同时，达到节约空间的目的。

状态压缩是一种优化动态规划算法的技巧，用于降低空间复杂度。当动态规划问题的状态转移方程只涉及到相邻状态时，我们可以使用状态压缩技巧将二维的dp数组转化为一维，从而减少所需的空间。通过状态压缩，我们可以将空间复杂度从O(N^2)降低到O(N)。然而，需要注意的是，状态压缩可能会降低代码的可读性，特别是对于初次接触优化后的代码的人来说。

动态规划算法的过程是随着阶段的增长，在每个状态维度上的分界点组成了DP拓展的轮廓。对于某些问题，我们需要在动态规划的状态中记录一个集合，保存这个轮廓的详细信息，以便于进行状态转移。若集合大小不超过 N ，集合中每个元素都是小于 k 的自然数，则我们可以把这个集合看做一个 N  位 k 进制数，以一个 [0,k^N-1] 之间的十进制整数的形式作为DP状态的一维。这种把集合转化为整数记录在DP状态中的一类算法被称之为状态压缩动态规划算法。
就是说，原来是一组数(不大于n），每个格子存数据，如果这个数据不大于k（首先是要不超过10，即十进制内能表示），那就用长为n的数来记录它，相当于用一个数来表示了一组数，相当于一个字符串记录，要读某一个数，就读这个串的某一位

常用为0，1即dp数组每位就记录01，那么就用一个数字来记录

Eg:小国王

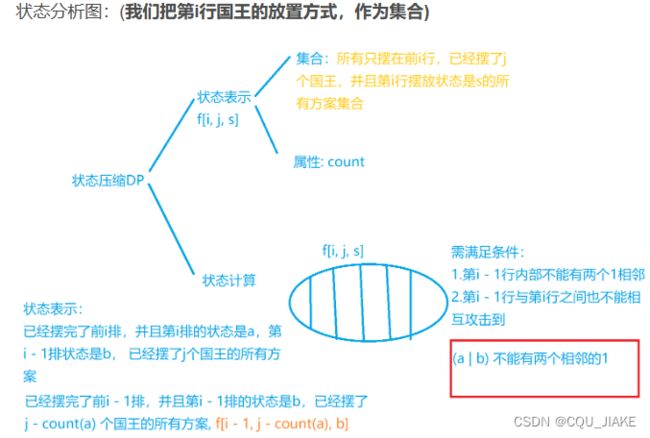
 从上一层分析就是说，保留上一层的信息，在第i层就有一些位置不能放，然后在此基础上放国王，使国王数量最多

问题是，每层都最优，最后结果一定最优吗？

只要任意王横坐标不相邻，就是合法状态；纵坐标不相邻，就是合法状态；

综合就是横纵都不相邻

让有国王的位置为1，没国王的位置为0，即状态为0100010 

>>即右移，表示读取这个数的第i位，

#include
#include
#include
#include
 
using namespace std;
typedef long long LL;
 
const int N = 12, M = 1 << 10,  K = 110;
 
int n, m;
vector state;
int cnt[M]; //状态state[a]的国王个数
vector head[M];//head[i] 里存储在第i行状态为state[a]的情况下，上一行状态可以取到的合法状态statep[b]
LL f[N][K][M]; //状态转移方程，存方案数
 
bool check(int state)
{
    for(int i = 0;i < n;i ++) //同一行两个国王不能相邻
        if((state >> i & 1) && (state >> i + 1 & 1))
            return false;
    return true;
}
 
int count(int state) //统计该状态下国王，即1的个数
{
    int res = 0;
    for(int i = 0;i < n;i ++) res += state >> i & 1;
    return res;
}
 
int main()
{
    cin >>n >> m;
    //预处理所有合法状态 (对于这两个状态压缩有疑惑的，看看上面的图)
    for(int i = 0;i < 1 << n;i ++)
        if(check(i))
        {
            state.push_back(i); //将合法方案存入state
            cnt[i] = count(i);
        }
        //预处理所有合法状态的合法转移
    for(int i = 0;i < state.size();i ++)
        for(int j = 0;j < state.size();j ++)
        {
            int a = state[i], b = state[j];
            if((a & b) == 0 && check(a | b)) //a & b 指第i行和i-1行不能在同列有国王， check(a|b) == 1 指i和i -1行不能相互攻击到
                head[i].push_back(j);  //head[i] 里存储在第i行状态为state[a]的情况下，上一行状态可以取到的合法状态statep[b]
        }
    f[0][0][0] = 1; //求方案数时，初始方案需要为1,因为全部空 也是一种方案
    for(int i = 1;i <= n + 1;i ++) //枚举每一行
        for(int j = 0;j <= m;j ++) //国王数量
            for(int a = 0;a < state.size();a ++) //枚举合法方案
                for(int b : head[a])
                {
                    int c = cnt[state[a]];  //状态state[a]的国王个数
                    if(j >= c)
                        f[i][j][state[a]] += f[i - 1][j - c][state[b]]; //f[i][state[a]], 在第i行状态为i时，所有i - 1行的状态数量
                    //因为state[a]和a呈映射关系，所也可以写成
                    //  f[i][j][a] += f[i - 1][j - c][b];
                }
        cout << f[n + 1][m][0] << endl;//我们假设摆到n + 1行，并且另这一行状态为0,那么即得到我们想要的答案， 
    //如果我们用f[n][m][]来获取答案，那么我们就要枚举最后一行的所有状态取最大值，来得到答案。
 

 例题： 最短Hamilton路径

0-1，即有还是没有，等式右边是说前一个状态，w[k][j]就是由k到j的权值，前一个状态，k记录此时的终点，也是权值的起点。state表示走到这里时，一共走了哪些点，最终是要全为1，采用状态压缩，就要每访问到一个节点，就要把原数都往前移一位，并在最后添个1，表示又多访问了一个点等式左边 

2704

P能放，放了后周围的P就不能放。目的是在地图中p放最多

暴力就是从头开始遍历，然后深搜，维护一个最大的炮兵数

双向搜索

3067

就是给定一个数组，然后找一个子数组，让子数组可以被划分

随便找两个数，然后在数组中找有没有这俩数的和，这是子数组有三个数的情况

随便找两个数，然后再随便找两个数，四个数

……

还是要递归去解决

每个数有三种状态，

1.不放入任何集合

2.放入左边集合

3.放入右边集合

直接暴力就是从数组第一个开始往后，复杂度为3^n

分两半，前一半放第一组的和为a，第二组放b，即a+b<=sum(n/2)

后一半同理，有a+c=b+d,则有a-b=c-d，即转变成了每半自己的一个关系

即统计每一半和为a-b的方案，

一个数被放入第一组中，a−b的值变大，在第二组中，a−b的值变小，如果不放，则a−b不变，所以维护a−b的值即可。