GoodFloorplan: Graph Convolutional Network and Reinforcement Learning-Based Floorplanning

GoodFloorplan: Graph Convolutional Network and Reinforcement Learning-Based Floorplanning
IEEE TRANSACTIONS ON COMPUTER-AIDED DESIGN OF INTEGRATED CIRCUITS AND SYSTEMS

摘要

电子设计自动化（EDA）包括一系列的计算困难的优化问题，需要大量的专业知识，以及相当数量的试错的努力。然而，开放的挑战，包括长的仿真运行时间和缺乏泛化，继续限制现有的EDA工具的应用。最近，基于学习的算法，特别是强化学习（RL），已成功地应用于处理各种组合优化问题，自动获取知识，从过去的经验。在这篇文章中，我们制定的布局规划问题，物理设计流程的第一阶段，作为一个马尔可夫决策过程（MDP）。提出了一种基于端到端学习的布图规划框架GoodFloorplan来探索设计空间，该框架结合了图卷积网络（GCN）和RL。实验结果表明，与最先进的启发式布图规划器相比，建议GoodFloorplan可以提供更好的面积和线长。

一、简介

在这篇文章中，我们专注于布图规划的问题，其中的目标是确定的位置的电路块，使芯片面积和线长最小化。作为物理设计流程的第一阶段，布图规划的质量显著影响后续的布局和布线。通常，布图规划的研究可以分为两类。一个类别是平面布置图表示的研究。对于具有切片结构[13]的布图规划，广泛使用二叉树表示，其叶子对应于块，并且内部节点定义两个对应后代的垂直或水平合并操作。对于更一般的非切片布图规划，开发了几种有效的表示，包括序列对（SP）[14]，有界切片网格（BSG）[15]，O树[16]，具有包装序列的传递闭包图（TCG-S）[17]和B* 树[18]。另一类是布图规划算法的研究。利用合适的布图表示和/或有效的扰动方法，可以通过线性规划[19]或通过一些元启发式算法（如模拟退火[20]、模因算法[21]和蚂蚁系统算法[22]）来实现高质量的布图。

虽然以前的工作已经调查布图规划算法，仍然存在两个主要问题。一个是专家知识可能不足手动启发式，由于大量的领域知识以及大量的试错是必不可少的这些方法的事实。更糟糕的是，这些算法不能保证良好的性能。然而，强化学习可以学习知识的环境，代理交互，因此，设计空间可以有效地探索。此外，通过在一个电路上训练RL代理，相同的代理可以直接应用于具有不同大小的新电路。以这种方式，仿真成本降低，而无需从头开始设计。

另一个挑战是算法可扩展性的限制。随着现代集成电路设计变得越来越复杂，更大规模问题的状态空间表示成为可扩展性的瓶颈。因此，当前的布图规划器遭受“维数灾难”，并且因此无法在大规模情况下进行优化[23]。受电路网表是一个图这一简单事实的启发，可以用图卷积网络来提取电路拓扑表示。通过将大型图的信息表示为低维向量，图卷积网络（GCN）使得能够在不同网表拓扑之间传递知识。

从根本上不同于以前的方法，我们提出了一个端到端的基于学习的布局规划框架GoodFloorplan，结合GCN和RL。因此，我们可以避免在搜索过程中引入太多的先验领域知识。此外，所提出的布图规划器在新的看不见的网表上的泛化也得到了改进。本工作的关键技术贡献如下：

1. 我们将布图规划公式化为RL问题，并提出了一个基于端到端学习的模型来解决这个问题
2. 利用一个优势演员-评论家算法，有效地探索布图规划的解决方案空间
3. 构建GCN以形成网表图嵌入
4. 实验结果表明，与最先进的启发式布图规划器相比，该框架可以提供更好的性能

二、准备工作

在这一部分中，我们首先介绍了强化学习的背景，然后给予了布图规划的问题形式化。

A. 强化学习
RL学习从状态到动作或动作分布的映射，以便最大化数字奖励[1]。典型地，RL可以被公式化为MDP，其由四个关键元素组成。
1)一组可能的环境状态S。
2)代理可以采取的一组动作A。
3)状态转移模型${P^a}_{s{s}^{\prime }}$表示在作用a ∈ A下状态s ∈ S到s’ ∈ S的转移概率。
4)奖励函数Ra s是在状态s ∈ S中采取行动a ∈ A的数值奖励反馈。
MDP通常依赖于马尔可夫假设，使得未来状态的概率分布仅取决于当前状态。换句话说，过去的状态序列不影响环境。图1示出了典型的MDP流。在每个时间步t，代理从状态$s_t$开始，在t采取行动，到达新的状态$s_{t+1}$，并从环境中获得奖励$r_t$。通过重复的情节（状态、动作和奖励的序列），智能体的轨迹被完全描述。MDP的目标是找到策略π，其是从状态空间到动作空间π的映射：S → A，最大化累积回报（收益）

其中γ是延迟未来奖励的折扣因子，t表示任何时间步长。此外，MDP的状态-值函数Vπ（s）是当在状态s中开始并且然后在其后遵循策略π时的预期回报，如下所定义：

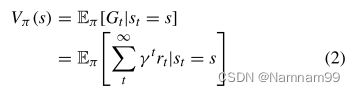
其中$E_{\pi }$ [ · ]表示给定代理遵循策略π的随机变量的期望值。类似地，状态-动作-值函数$Q_{\pi }$（s，a）被定义为从状态s开始、采取动作a并且此后在策略π下表现的预期回报。

RL方法可以分为两类：1）基于模型的方法和2）无模型方法。在基于模型的RL算法中，我们不仅从通过与环境交互生成的经验中学习策略或值函数，而且还显式地创建环境的模型（即，状态转移概率和回报函数）。在无模型强化学习中，我们并没有明确地学习MDP模型，而是只尝试学习一种策略来确定哪些行为会产生最大的累积奖励。由于无模型方法更容易收敛，因此在大多数现有的强化学习工作中被广泛使用。典型的无模型RL方法包括Q学习[24]和一些策略梯度算法，如REINFORCE [25]和actor-critic [26]。

B 平面规划的定义
设B ={$b_i$| 1 ≤ i ≤ n}是矩形块的集合，其中每个块$b_i$具有指定的宽度$w_i$和高度$h_i$，并且N ={$n_i$| 1 ≤ i ≤ m}表示网表，其中每个网描述块之间的连接。布图规划是将元组（$x_i$，$y_i$）分配给每个块$b_i$，使得实现以下条件。
1)任何两个块之间没有重叠。
2)一些目标，例如，面积和线长，被最小化。基于面积函数A（·）和线长函数W（·），优化目标定义如下：

其中$f_p$是可行的布图规划解，并且η表示系数。在这项工作中，面积函数在（5）中给出，它考虑了固定轮廓约束:

其中W和H是布图规划的当前宽度和高度，$E_W$ = max{W-$W_0$，0}和EH = max{H-$H_0$，0}是考虑固定轮廓约束时布图规划的过大宽度和高度，λ是布图规划的纵横比，C1和C2是用户定义的常数。根据[27]中的实验配置，C1 = 1且C2 = 1/16。使用这个公式，我们不仅处罚更大的过度宽度和过度高度，但保持区域项目有效时，与其他目标相结合。此外，我们采用半周长线长模型（HPWL），这是最常用的线长计算近似[28]。由于面积和线长的大小不同，我们对这两个目标进行了归一化。

在这项工作中，我们采用了经过充分研究的SP [14]作为平面图表示。定义1（序列对）：一个SP（1，2）是表示n个块的列表的n个元素的序列对，其如下定义每对非重叠块之间的几何关系：

给定SP，首先构建水平和垂直约束图[14]。然后，可以通过最长路径长度计算来导出所得到的布图规划。注意，对于n个块，布图规划配置编号是$n^2$。提出SP的原始论文提供了O（$n^2$）算法来将SP转换为平面图。为了加速该过程，Tang et al.[29]通过计算加权最长公共子序列，进一步提出了一个O（nloglogn）的求值算法。例如，图2中示出了SP的对应的布图规划<413652><612345>。

三、问题描述

在这项工作中，我们的目标的布局规划问题，其中的目标是确定一个平面的位置分配电路块，使芯片面积和线长最小化。利用许多局部搜索启发式来生成布局平面图，不同于以往的工作，专注于平面图的建设，我们探讨了学习本地搜索启发式通过多个过去的搜索经验的可能性。更具体地说，我们的目标是从零开始获得一个本地搜索算法，而无需在平面图探索过程中引入任何先验人类知识。因此，高质量的布图规划可以通过有效的局部搜索启发式实现。

模拟退火是一种用于处理优化问题的流行局部搜索元启发式算法[30]。在以下描述中，令S为解（状态）空间f：S → R是定义在解空间上的目标函数，N（s）是s ∈ S的邻域函数。模拟退火通常从初始解s ∈ S开始。在每一步中，当前解s的相邻解s ∈ N（s）然后通过一些预先指定的扰动进行采样。大都会准则根据下式确定系统从当前解s移动到候选对应物s的接受概率：

其中f（·）是在⑷中定义的目标函数，并且tk表示第k次迭代时的温度值。大都会准则最终导致系统向成本较低的状态转移。为了通过局部搜索探索更好的布图规划，我们定义以下MDP：

1.状态空间：对于布图规划问题，状态s是布图规划解决方案，其包含完整的SP以及每个块的取向。
2.行动空间：通过一些预先指定的扰动产生相邻的布图规划解决方案。在这项工作中，我们定义了五种类型的扰动如下：

• a）交换1中的随机块对。
• b）在2中交换一对随机的块。
• c）交换1和2中的随机块对。
• d）将随机选择的块移动到1和2中的新位置。
• e）将随机选择的块旋转90◦。
  在对相邻的布图规划进行采样之后，RL代理确定接受邻居或拒绝移动。因此，动作空间大小等于2。

3)状态转换：给定平面布置方案（状态），上述扰动方法中的任一种肯定会使代理移动到另一状态。因此，它简化了我们的MDP公式中的概率设置。
4)奖励：我们在布局规划问题中的目标是最小化面积和线长。由于代理试图最大化总奖励，最大化累积奖励的动作应该与布局规划问题的目标一致。

在这项工作中，我们使用的目标成本的减少作为奖励。也就是说，只要找到更好的解决方案，就分配奖励;对于更差的解决方案，将奖励响应设置为0。此外，此外，我们通过除以初始解的成本将奖励归一化为[0，1]。

其中f（·）是（4）中所示的目标函数。s是当前解（状态），而s是s的相邻解。根据（7），最大化总回报等价于最小化目标成本。利用上述知识，我们将布图规划局部搜索问题公式化如下:

问题1：给定上述MDP模型，RL代理将找到最佳策略π *，使得平面图的面积和线长最小化。

四、流程框架

在本节中，首先描述所提出的基于端到端学习的网络架构。然后，我们定义网络输入，以指导代理作出决定。接下来，开发GCN以生成网表的特征嵌入。最后，我们提出了如何使用策略梯度算法来学习最优策略。

整体网络架构

如上所述，RL代理学习找到生成从状态空间到动作空间的映射的最优策略。构造这样的策略的直观方式是存储每个可能状态的最佳动作。然而，对于具有n个块的布图规划，假设引脚位于块的中心，则存在$(n!{)}^2\cdot 2^n$不同的状态。在这种情况下，我们不能期望找到最优策略或最优值函数。相反，可以利用神经网络来近似最优策略。但是训练这样一个网络是一个巨大的挑战，因为包含所有可能布局的状态空间是巨大的。另一方面，不同的网表具有非常不同的属性，包括不同数量的块、块大小和各种图形拓扑。为了解决这一挑战，我们提出了一个端到端的网络架构，如图3.所示。

为了提取有关网表的信息，开发了一种新的图神经网络，该网络由三个图卷积层组成，其维数分别为12，12和5。图卷积运算的过程在第IV-C节中示出。在最后一层，对所有节点执行约简均值函数，以实现网表图的整体嵌入。我们将图神经网络作为编码器纳入网络架构。结果，网络能够在推断时间将与新的未见网表相关联的信息编码成有意义的信号。

给定网表图嵌入和其他设计的状态特征，我们首先将它们连接成1-D向量。注意，其他设计的状态特征包含成本相关的统计信息、搜索步骤等。如第IV-B节所述。然后，将1-D向量输入到具有四个全连接层的策略网络，并且在除了最后一层之外的所有层之后插入ReLU（·）作为激活函数。结果，可以实现关于动作的概率分布${\pi }_{\theta }(a|s)$.。

GoodFloorplan框架示意图：GCN编码关于网表图的信息，策略网络和价值网络分别输出动作的概率分布和当前布局的预期回报的估计。

通过政策网络。这里，θ是策略网络的参数向量。最后，可以基于该分布对给定状态s的最优动作a进行采样。此外，我们还实现了一个具有参数向量φ的价值网络Vφ（s），以估计每一步的预期回报。如图所示。正如图3所示，价值网络包括三个全连接层，并且网表图和设计状态特征的级联被传递到网络。主要原因是网表图统计量和其他设计的状态特征可以共同为状态值估计提供可信信息。

输入的特征信息

如上所述，我们寻找紧凑布局的解决方案。在执行每种类型的扰动之后，代理选择动作。因此，环境的信息应该被馈送到模型以分别生成动作的分布和当前布局的预期回报的估计。在这篇文章中，我们提出了以下决策特征。
1)当前状态的目标成本。
2)到目前为止最低和平均的目标成本。
3)采样的相邻状态的目标成本。
4)受扰动块的面积和其他受影响块的数量。
5)表示当前步骤的标量。
6)网表图（图邻接矩阵和节点特征）。

首先，布图规划搜索的主要目标是找到具有最小成本的状态。给定当前状态s和采样邻居s代理基于在（4）中定义的布局成本来决定接受邻居或拒绝移动。因此，我们提供了一组与成本相关的统计信息，以指导代理采取更好的决策，如前三个状态特征所示。

其次，每个扰动方法可以使代理移动到另一个状态。为了量化移动的影响，采用受扰动块的面积和其他受影响块的数量。受影响的块指示其坐标受受扰动的块影响。第三，局部搜索的搜索进度具有与温度调度类似的效果。因此，我们还将当前步骤作为一个特征包括在内。

最后，布图规划的输入包含网表图。图4（a）示出了具有六个网的门级网表，$n_l$ ={A，C，E}，$n_2$ ={B，C，D}，$n_3$ ={C，E，F}，$n_4$ ={D，F}，$n_5$ ={E，G}，以及$n_6$ ={F，G，H}。请注意，不考虑I/O端子。网表中大小为k的每个网形成k-团，并且团中的所有边接收2/k的权重[31]。对应的基于无向团的图模型G（V，E）在图1中描绘。图4（B），其中每个节点v ∈ V表示电路块，并且每个边e ∈ E表示两个节点之间的连接。在这项工作中，我们使用图神经网络来生成输入网表的特征嵌入，这在第IV-C节中详细解释。因此，代理可以学习推广到新的不可见网表的模式。所有特征都被归一化为[-1，1]或[0，1]，以便于训练。为此，我们将初始状态的目标成本表示为$e_0$，并通过min（1，f/$e_0$ − 1）对所有成本相关项进行归一化。此外，上述特征将被连接成单个向量表示，然后传递到下游网络。

图特征嵌入

基于图的学习是机器学习的一种新方法，具有广泛的应用[32]。在执行某个任务之前，应该首先获得节点或图的表示，这被称为嵌入，并且可以馈送到下游模型。对于布图规划问题，网表可以表示为无向图，如图4.因此，我们利用GCN来提取网表图的特征，并将GCN作为编码器并入到所提出的端到端网络架构中，如图所示3。结果，网络能够在推断时间将与新的未见网表相关联的信息编码成有意义的信号。

图节点的初始特征是6-D向量[sz，w，h，x，y，ut]。[sz，w，h，x，y]分别表示对应块的面积、宽度、高度、X坐标和y坐标。UT对应于块利用率，其通过块面积与布局图的总面积的比率来计算。然后，节点嵌入通过三个连续的图卷积层。在这项工作中，我们实现了一个类似于GraphSAGE [33]的GCN来生成节点嵌入。基本过程由两个步骤组成，即，聚合和编码，其可以被公式化为

其中（8a）中的$AGGREGAT{E}_l$是层l中的聚合器函数，其被应用于每个节点v的邻域节点。聚合相邻特征向量后，我们首先将节点v的当前表示$h_v^{l-1}$与聚合的邻域向量$h_{N(v)}^l$连接起来。然后，对级联向量执行由嵌入投影和非线性激活函数σ（·）组成的编码操作，如（8b）所示。$W^l$是层l中的权重矩阵。结果被传递到下一个图卷积层。

在图1中描绘了图示用于生成节点1的嵌入的2层GCN的示例。5，其中层$l_1$和$l_2$中的编码维度分别为$d_1$和$d_2$。首先，在图卷积层11中，通过聚合每个节点的原始特征和邻居的特征来生成每个节点的隐藏表示。例如，在节点1中通过聚合其自身和邻居节点2-4的特征来执行聚合器功能。在特征聚合之后，对每个节点应用非线性变换以产生具有维度$d_1$的新特征。然后在层$l_2$中进行相同的聚合和编码操作。结果，节点1的最终隐藏表示从另一个邻域接收消息。

具体地，如果选择均值函数作为聚合器函数，则层1中的聚合和编码的过程等效于以下：

其中A是图的邻接矩阵，并且$H^l$表示图中每个节点的嵌入。此外，$c_{ij}$表示边的权重。注意，$c_{ij}$的值等于$c_{ji}$。最后，整个图的嵌入被计算为最终图卷积层处的所有节点嵌入的平均值。

基于梯度的优化策略

我们使用策略梯度RL算法，优势演员-评论家（A2C），学习的政策。注意，A2C算法是异步优势行动者-批评者（A3C）策略梯度方法的同步版本[34]。在A2C算法中，批评者被训练为使用时间差学习来近似状态值，而行动者被训练为在批评者指导的方向上改进策略。因此，考虑到一步返回，用以下均方误差训练评论家：

其中Vφ（·）是具有参数φ的近似值函数，并且$s_{t+1}$是在状态$s_t$之后遇到的状态。基于损失函数，利用梯度下降算法如下更新决策时刻t中的临界点：

其中${\alpha }^{\phi }$是学习率，并且$A_t（s_t，a_t）$是优势函数的估计。同时，行动者被训练来最大化累积奖励的期望。

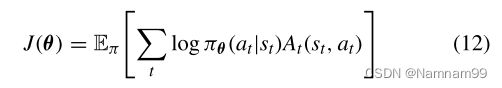
其中θ是策略网络的参数。通过梯度上升算法，根据以下内容更新演员：

其中${\alpha }^{\theta }$是学习率，${\theta }_t$是决策时刻t的策略网络权重。由于A2C方法学习一个显式的随机策略，可以有效地探索行动空间。此外，由于作为状态相关基线的临界点，降低了梯度方向估计的方差。

算法1给出了解决布局局部搜索问题的A2C算法的高级描述。首先，在初始化阶段，首先初始化策略参数θ和状态值权重Φ（第1行）。两个学习率，记为${\alpha }^{\theta }$和${\alpha }^{\phi }$，分别设置为6 × 10−4和5 × 10−3（第2行）。然后，在每个片段的开始，随机地产生第一状态$s_1$（第4行）。在每个时间步长t，给定当前状态$s_t$，从概率分布${\pi }_{\theta }（a_t）$中由actor采样动作at（line 6）。作为回报，代理接收标量奖励rt，并根据奖励函数和状态转换模型转移到下一个状态st+1，这在第III节（第7行）中描述。如（11b）（第8行）所示，评价器还根据回报信号$r_t$和其状态值估计的变化产生一步时间差TD（0）误差。与资格跟踪方法相比，一步时间差方法是完全在线和增量的，从而避免了复杂性[1]。最后，行动者基于其从批评者接收的TD（0）误差来调整策略参数θ，同时批评者还使用相同的误差来更新状态值权重φ（第9行和第10行）。因此，演员-评论家的方法可以减少学习过程中的方差。此外，由于GCN是网络架构的骨干，因此策略网络和价值网络的梯度信息将一起反向传播到GCN以更新其权重参数。

四、实验结果

略

结论

在本文中，我们提出了一个创新的基于端到端学习的布局规划框架GoodFloorplan，其中GCN被纳入RL。我们首先采用GCN生成的电路网表图的特征嵌入。然后，基于网表图嵌入和其他设计的状态特征，我们使用的策略网络和价值网络学习的最优策略。实验结果表明，与现有的基于启发式的方法相比，所提出的GoodFloorplan可以减少面积消耗和线长。