PyTorch深度学习-梯度下降算法

学习视频链接（刘二大人）：https://www.bilibili.com/video/BV1Y7411d7Ys
分治法：搜索时先进行稀疏搜索，相当于求局部最优点

梯度下降算法：得到的不一定是全局最优，但一定是局部最优的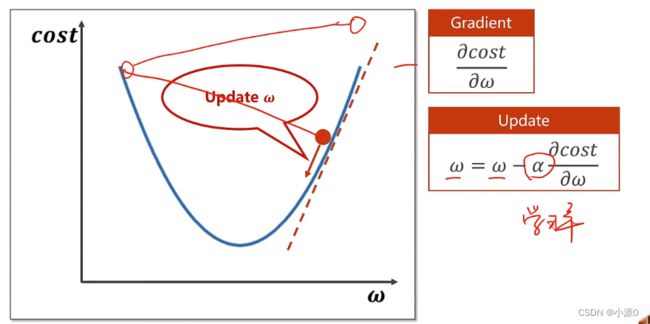
更新权重的方法：Update，学习率越小越好
鞍点：梯度为0（鞍点会导致权重w无法进行迭代）
梯度下降算法代码实现：

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1

def forword(x):
    return x * w

# 求cost
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forword(x)
        cost = cost + (y - y_pred) * (y - y_pred)
    return cost / len(xs)

# 梯度
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        y_pred = forword(x)
        grad = grad + 2 * (y_pred - y)
    return grad / len(xs)

# 训练过程
print("Predict (after training)", 4, forword(4))
for epoch in range(100):
    # 设置进行100轮训练
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w = w - 0.01 * grad_val
    print("Epoch:", epoch, "w=", w, "loss=", cost_val)
print("Predict (after training)", 4, forword(4))

cost如果先下降再上升，即训练发散，常见原因：学习率太大
梯度下降算法用的比较少，随机梯度下降算法是梯度下降算法的一个引申

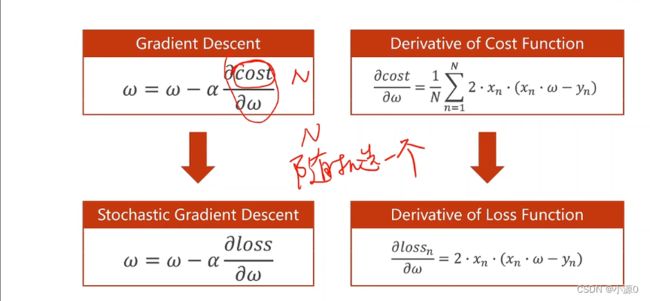
如果函数为一个带有鞍点的损失函数，如果每次只用其中一个样本，但每个样本都有噪声，则引入随机噪声，引入随机性，更新的过程时，就有可能跳过鞍点。
随机梯度算法实现代码如下：

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forword(x):
    return x * w

# 求cost
def loss(x, y):
    y_pred = forword(x)
    return (y_pred - y) ** 2

# 梯度
def gradient(x, y):
    y_pred = forword(x)
    return  2 * x * (y_pred - y)

# 训练过程
print("Predict (after training)", 4, forword(4))
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        # 每次的x与其他x无任何依赖关系
        grad = gradient(x, y)
        w = w - 0.01 * grad
        print("\t grad:", x, y, grad)
        # 计算现在的损失
        l = loss(x, y)
    print("progress:", epoch, "w=", w, "loss=", l)
print("Predict (after training)", 4, forword(4))