【数据结构】二叉树
作者主页:paper jie_博客
本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。
本文录入于《JAVA数据结构》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造,将javaSE基础知识一网打尽,希望可以帮到读者们哦。
其他专栏:《算法详解》《C语言》《javaSE》等
内容分享:本期将会分享数据结构中的难点二叉树
目录
树形结构
什么是树形结构
重要概念
树的表示形式
树的应用
二叉树
什么是二叉树
二叉树的性质
二叉树的存储
二叉树的基本操作
二叉树的遍历
前中后序遍历
层序遍历
树形结构
什么是树形结构
树是一种非线性的数据结构,它是由n(>=0)个有限节点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一个根朝上,叶朝下的倒挂树。
特点:
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根结点外,其他结点被分为m个互不相交的集合
树是递归定义的
注意:树形结构中,子树是不能有交集的,否则就不是树形结构
重要概念
结点的度:一个结点含有子树的个数称为该结点的度
树的度:一棵树中,所有结点度中的最大值为该树的度
叶子结点:度为0的结点称为叶结点
父结点:如果一个节点有子结点,则这个结点被称为父结点
子结点:一个结点含有的子树的根结点称为该结点的子结点
根结点:一课树中,没有父结点的结点
结点的层次:从根结点开始定义起,根为第一层,根的子结点为第二层,依次类推
树的高度或深度:树中结点的最大层次
非终端结点或分支结点:度不为0的结点
兄弟结点:具有相同父结点的结点互称为兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟
结点的祖先:从根到该结点所经分支上的所有结点
子孙:以某结点为根的子树中任一结点都称为该结点的子孙
森林:由m(m>=0)棵互不相交的树组成的集合称为森林
树的表示形式
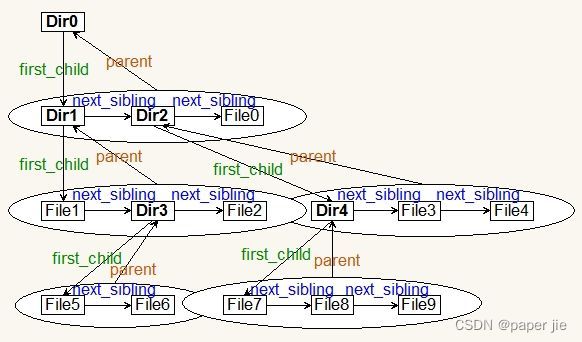
树的结构相对线性表比较复杂,要储存表示起来比较麻烦,实际中树有许多表示方法:双亲表示法,孩子表示法,孩子双亲表示法,孩子兄弟表示法等等。下面写一种最常用的孩子兄弟表示法。
class Node {
int value; // 树中存储的数据
Node firstChild; // 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}树的应用
一般我们文件系统管理就是用树形结构来处理的
二叉树
什么是二叉树
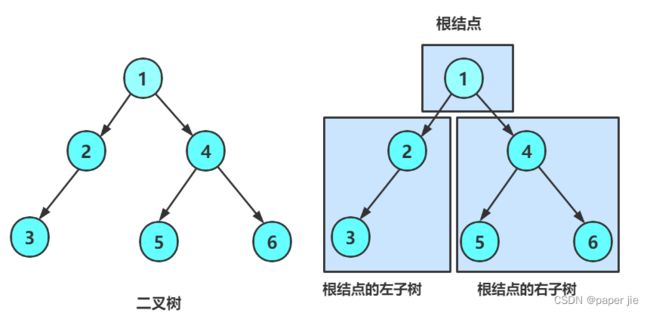
一颗二叉树是结点的有限集合,这个集合:
可能为空
可能是由一个根结点加上两颗左子树和右子树的二叉树组成的
注意:
二叉树不存在度大于2的结点
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
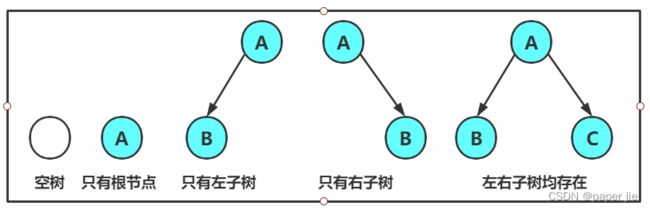
二叉树有几种情况复合而成:
二叉树的性质
若根结点的层数为1,则一颗非空的二叉树的第i层上最多有2^(i-1)个结点
若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2^k - 1
对任何一个二叉树,如果其叶结点个数为n0,度为2的非叶结点的个数为n2,则有n0 = n2 + 1
具有n个结点的完全二叉树的深度K为log2(n+1)向上取整
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有结点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1
若2i+2
二叉树的存储
二叉树的存储结构分为:顺序存储和链式存储
二叉树的链式存储是通过一个一个节点引用起来的,通常表示的方式有二叉和三叉表示方式
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}二叉树的基本操作
下面是二叉树一些基本功能的代码:
public class BinaryTree {
static class TreeNode {
char val;
TreeNode left;
TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
return A;
}
//前序遍历
public void preOrder(TreeNode root) {
if(root == null) {
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}
//中序遍历
public void inOrder(TreeNode root) {
if(root == null) {
return;
}
preOrder(root.left);
System.out.print(root.val+" ");
preOrder(root.right);
}
//后序遍历
public void lastOrder(TreeNode root) {
if(root == null) {
return;
}
preOrder(root.right);
preOrder(root.left);
System.out.print(root.val+" ");
}
//求tree的节点个数
int Treesize;
public int size(TreeNode root) {
if(root == null) {
return 0;
}
Treesize++;
size(root.left);
size(root.right);
return Treesize;
}
public int size1(TreeNode root) {
if(root == null) {
return 0;
}
return size1(root.left) + size1(root.right) + 1;
}
// 获取叶子节点的个数
int getLeafNodeCount(TreeNode root) {
if(root == null) {
return 0;
}
if(root.left == null && root.right == null) {
return 1;
}
return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);
}
// 获取第K层节点的个数
int getKLevelNodeCount(TreeNode root, int k) {
if(root == null) {
return 0;
}
if(k==1) {
return 1;
}
return getKLevelNodeCount(root.left, k-1) + getKLevelNodeCount(root.right, k-1);
}
// 获取二叉树的高度
int getHeight(TreeNode root){
if(root == null) {
return 0;
}
int a = getHeight(root.left);
int b = getHeight(root.right);
return a > b ? a+1 : b+1;
}
// 检测值为value的元素是否存在
TreeNode find(TreeNode root, char val) {
if(root == null) {
return null;
}
if(root.val == val) {
return root;
}
TreeNode leftNode = find(root.left, val);
if(leftNode != null) {
return leftNode;
}
TreeNode rightNode = find(root.right, val);
if(rightNode != null) {
return rightNode;
}
return null;
}二叉树的遍历
前中后序遍历
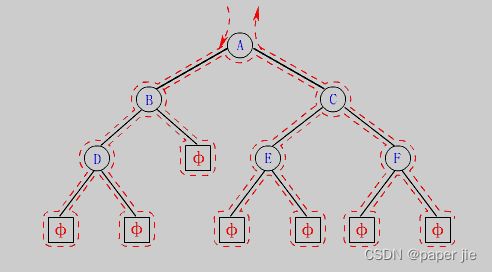
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
具体代码:
//前序遍历
public void preOrder(TreeNode root) {
if(root == null) {
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}
//中序遍历
public void inOrder(TreeNode root) {
if(root == null) {
return;
}
preOrder(root.left);
System.out.print(root.val+" ");
preOrder(root.right);
}
//后序遍历
public void lastOrder(TreeNode root) {
if(root == null) {
return;
}
preOrder(root.right);
preOrder(root.left);
System.out.print(root.val+" ");
}层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历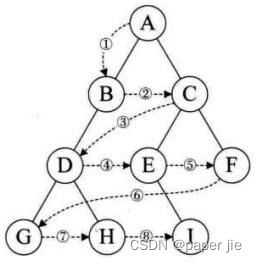
具体代码:
class Solution {
public List> levelOrder(TreeNode root) {
List> array = new ArrayList<>();
if(root == null) {
return array;
}
Queue queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
List tmp = new ArrayList<>();
int size = queue.size();
while(size != 0) {
TreeNode x = queue.poll();
tmp.add(x.val);
size--;
if(x.left != null) {
queue.offer(x.left);
}
if(x.right != null) {
queue.offer(x.right);
}
}
array.add(tmp);
}
return array;
}
}