数组之滑动窗口系列
Sliding window algorithm is used to perform required operation on specific window size of given large buffer or array.
滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作。
This technique shows how a nested for loop in few problems can be converted to single for loop and hence reducing the time complexity.
该技术可以将一部分问题中的嵌套循环转变为一个单循环,因此它可以减少时间复杂度。
即我们要维护这样的一个窗口,窗口中存放着符合题目要求的字符串或者数组,我们通过对这个窗口内的字符串或者数组进行管理,来进行相应的优化(如记录最大长度,出现次数等)。
那么我们接下来来看几个题:
713. 乘积小于K的子数组(滑动窗口)
给定一个正整数数组 nums。
找出该数组内乘积小于 k 的连续的子数组的个数。
示例 1:
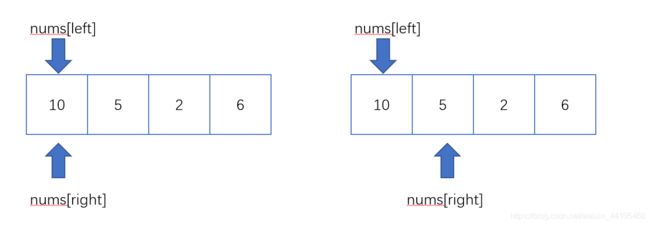
输入: nums = [10,5,2,6], k = 100
输出: 8
解释: 8个乘积小于100的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于100的子数组。
思路:
1.维护一个窗口,用于处理满足要求的子数组,当前子数组满足要求后,尝试将窗口扩大
2.若窗口扩大使得窗口中的子数组不再满足要求,那么需要动态地调整窗口,使其重新满足要求。
按照前面介绍的滑动窗口,我们此时需要维护一个窗口,窗口中存放符合要求的数组,这里的符合要求即为乘积<100
换句话说,只要窗口内数组的乘积小于100,我们就对个数做记录,但当窗口中的数组不满足要求时,我们要对窗口作维护。
本题中,数组中的元素全部为正整数,因此当乘积小于100时,我们需要记录出现的个数并继续扩大窗口。
而当乘积大于等于100时,只需不断地将窗口缩小,使窗口中的元素重新满足要求即可。
按照这个思路写出如下代码:
public int numSubarrayProductLessThanK(int[] nums, int k) {
//滑动窗口,记录当前遍历数组的左指针和右指针,动态记录满足要求的数组的个数
if (k <= 1) return 0;//数组中的数字均为整数,如果给的值为0或者更小,则无需计算
int prod = 1, ans = 0, left = 0;//prod初始值为1,用于与nums[i]的元素作积,ans表示最终结果,left为左指针
for (int right = 0; right < nums.length; right++) {//right为右指针
prod *= nums[right];//先保持左指针不动,右指针动态记录当前的乘积,做满足要求,记录此时的数组长度
while (prod >= k) prod /= nums[left++];//如果乘积超过目标值,除掉左边的值,同时使左指针+1,直至满足要求
ans += right - left + 1;//对于当前的k,包含right-left+1个满足要求的数组(这里不会存在重复的问题,因为不包含前面的数组)(只记[right]和[left,right])(已经吧前面的减去了,遍历完毕就是最终结果)
}
return ans;
}
再来看一道类似的题目:
1099. 小于 K 的两数之和
给你一个整数数组 nums 和整数 k ,返回最大和 sum ,满足存在 i < j 使得 nums[i] + nums[j] = sum 且 sum < k 。如果没有满足此等式的 i,j 存在,则返回 -1 。
示例 1:
输入:nums = [34,23,1,24,75,33,54,8], k = 60
输出:58
解释:
34 和 24 相加得到 58,58 小于 60,满足题意。
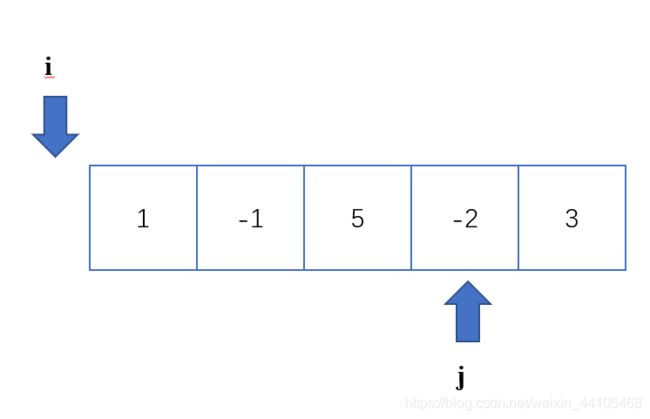
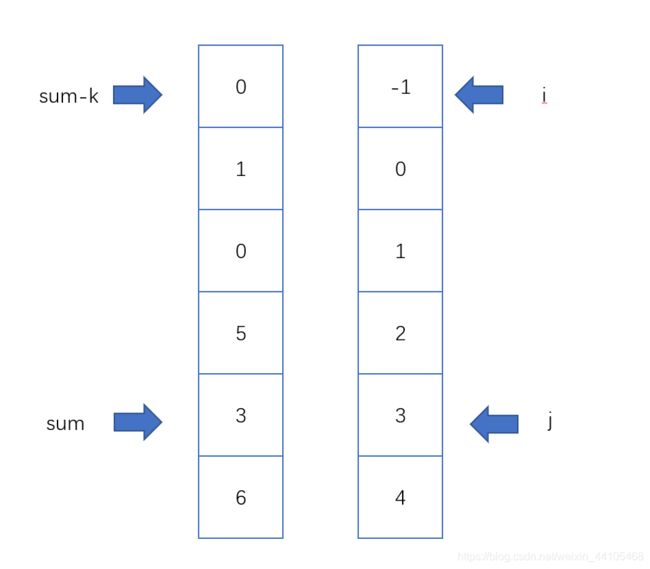
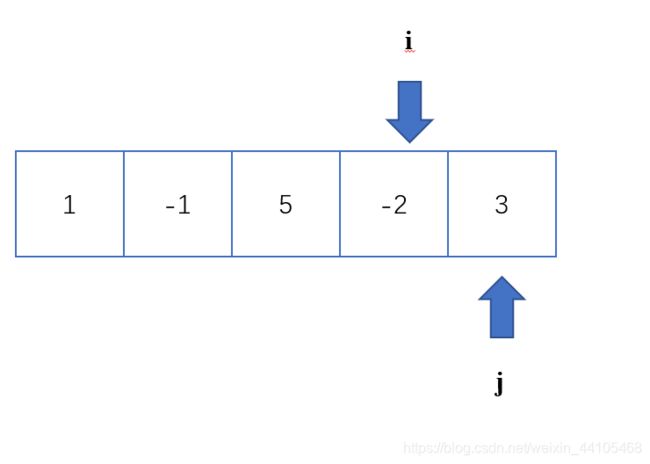
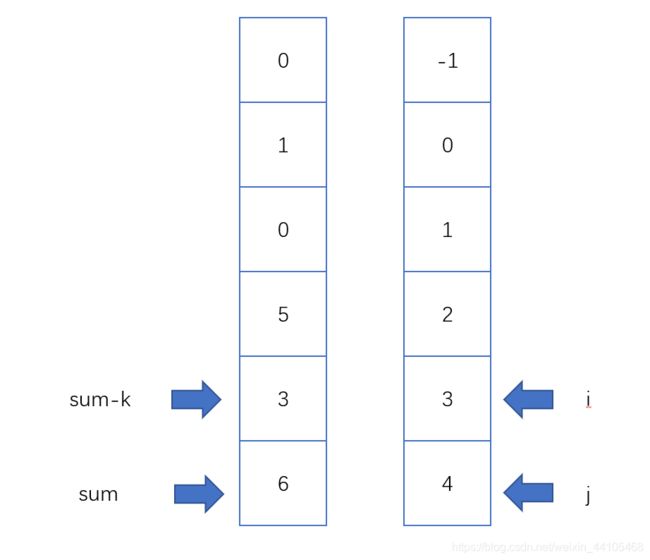
从题目中,我们可以看出,满足题目要求的结果是nums[i]+nums[j] 因此,我们必须要先对数组排序,使数组有序,然后用i,j两指针分别从首尾进行移动,当nums[i]+nums[j]>=k时,从窗口中移除nums[j],并将nums[j-1]加入窗口。 nums[i]+nums[j] public int twoSumLessThanK(int[] nums, int k) { Arrays.sort(nums); int left=0; int right=nums.length-1; int res =-1; while(left int sum =nums[left]+nums[right]; if(sum >=k){ right--; }else{ res =Math.max(res,sum); left++; } } return res; } 209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。 思路与前面的题目类似,维护一个用于接收满足target>=7的窗口 在满足target=7后,尝试将窗口扩大,扩大后若不满足要求,应调整窗口 本题中,nums[]中均为正数,因此若sum sum>=target时,应记录此时长度,并将窗口缩小 public int minSubArrayLen(int target, int[] nums) { //本题采用滑动窗口的方法,即两个指针ij,j指针右移进行遍历,当遇到元素总和大于等于目标值的情况时,记录此时数组的长度并进行动态比较,之后让i指针左移,然后从总和中减去nums[i]的值 int result=Integer.MAX_VALUE;//接收结果 int i=0;//指针1 int num=0;//记录总和 for(int j=0;j num+=nums[j]; while(num>=target){//注意此处应该写while因为j索引元素太大时,可能只滑动一个窗口依然会存在nums>target的情况 int sublength=j-i+1; result=result num-=nums[i++]; } } return result==Integer.MAX_VALUE? 0:result; } } 325. 和等于 k 的最长子数组长度 给定一个数组 nums 和一个目标值 k,找到和等于 k 的最长连续子数组长度。如果不存在任意一个符合要求的子数组,则返回 0。 示例 1: 输入: nums = [1,-1,5,-2,3], k = 3 与上个题的最大区别在于,nums[]中存在负数,使得窗口中元素不满足sum=target时,无法判断窗口应该如何移动。因为我们无法判断出窗口最左端的数是正数还是负数,就没法根据target与sum的关系进行动态调整。 因此,本题要额外使用一个hashMap来存储每个索引处的元素和,对于每个元素和sum,判断sum-k是否在hashMap中出现过,如果出现过,必然存在一个区间使得这个区间中的元素和满足sum=target,我们需要记录这个区间中数组的长度。 如图所示,我们可以根据sum-k在map中存在的位置定位到相关区间,通过i与j动态维护最长的自区间的长度。 public int maxSubArrayLen(int[] nums, int k) { Map int sum=0; //用于接收元素和 int ans=0; //接收最大长度 for(int i=0;i sum+=nums[i];//当前位置元素和 if(sum==k){ ans=i+1;//sum第一次为k时 } if(map.containsKey(sum-k)){ ans=Math.max(ans, i-map.get(sum-k)); } if(!map.containsKey(sum)){ map.put(sum, i); } } return ans; } 325. 和等于 k 的最长子数组长度 给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。 示例 1: 输入: nums = [0,1] 数组中只会出现1和0,那么可以仿照上个题,求索引i处的元素和,这里面如果nums[i]为0,sum-1,nums[i]为1,则sum+1,这样一旦某个区间出现了相同的1和0,那么这个区间的总和为0,也就是说如果某一索引处的sum为k,那么只要这个k在map中再次出现,则说明存在着有相等的1和0的区间。 public int findMaxLength(int[] nums) { Map map.put(0,-1);//首位置的前缀和为0 int cnt=0;//用于记录当前数值的总和 int maxLength=0;//用于记录最大长度 for(int i=0;i cnt+=(nums[i]==0?-1:1);//nums[i]为0或1时分别进行赋值 if(map.containsKey(cnt)){//因为0和1的和为(-1+1)=0,因此再次出现相同值时,一定是出现过01,此时动态记录长度 maxLength=Math.max(maxLength, i-map.get(cnt)); }else{ map.put(cnt, i); } } return maxLength; }
输出: 4
解释: 子数组 [1, -1, 5, -2] 和等于 3,且长度最长。
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。