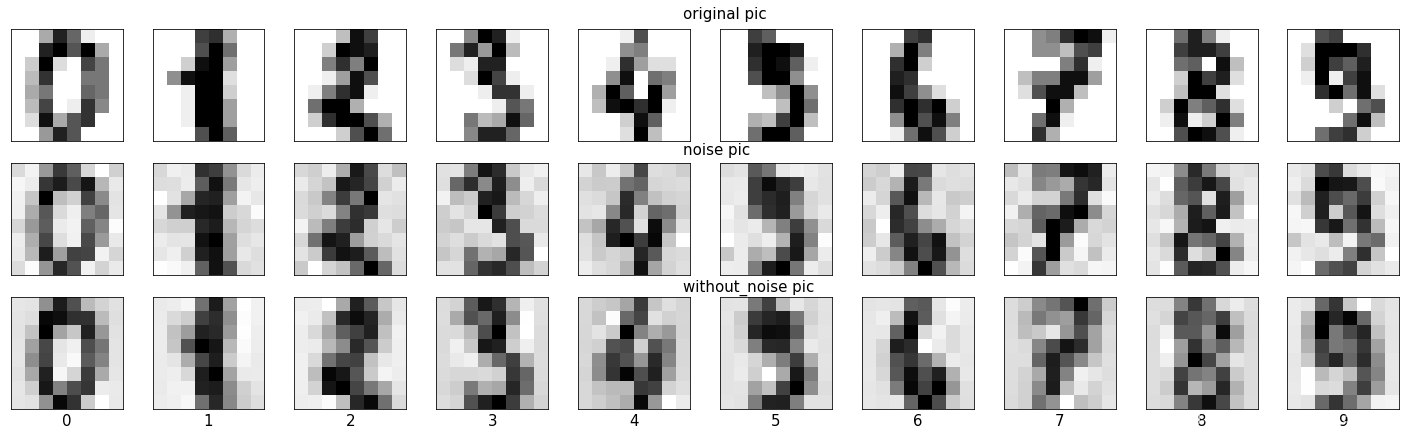PCA+SVD降维：完整代码+实例分析

import warnings
warnings.filterwarnings("ignore")
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np

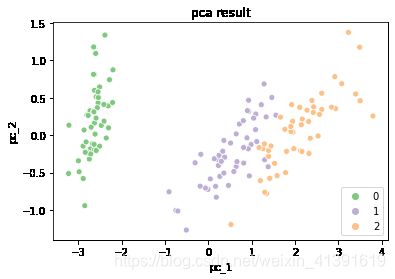
1.引例：鸢尾花数据集降维及可视化

x = load_iris().data
y = load_iris().target
x.shape #一共150个样本，4个特征

(150, 4)

pca = PCA(n_components=2) #将4个特征降成2个特征，以便在平面上展示
x_pca = pca.fit_transform(x)

# 降维结果的可视化
plt.figure()
sns.scatterplot(x_pca[:,0],x_pca[:,1],hue=y,palette=sns.color_palette("Accent", 3))
plt.title('pca result')
plt.xlabel('pc_1')
plt.ylabel('pc_2')
plt.show()

ps:sns.color_palette的可选值请戳sns的color_palette.

#属性explained_variance_，查看降维后每个新特征向量上所带的信息量大小（可解释性方差的大小） 
pca.explained_variance_

array([4.22824171, 0.24267075])

#属性explained_variance_ratio，查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比 
#又叫做可解释方差贡献率 
print(pca.explained_variance_ratio_)
print('降维后的信息量是原始信息量的{:.2%}'.format(pca.explained_variance_ratio_.sum()))

[0.92461872 0.05306648]
降维后的信息量是原始信息量的97.77%

2.PCA重要参数、属性、方法

2.1 重要参数

• n_components:降到多少维。可以填入整数、0-1之间的小数或者‘mle’
  0~1之间的小数表示保留多少信息量，根据信息量决定降到多少维，必须搭配 svd_solver='full’来使用；
  ‘mle’使用极大似然估计判断要降到多少维

• svd_solver:可选值‘auto’、‘full’、‘arpack’、‘randomized’;具体区别如下：
  auto：基于X.shape和n_components的默认策略来选择分解器：如果输入数据的尺寸大于500x500且要提 取的特征数小于数据最小维度min(X.shape)的80％，就启用效率更高的”randomized“方法；否则，就使用‘full’模式，截断将会在矩阵被分解完成后有选择地发生
  full：从scipy.linalg.svd中调用标准的LAPACK分解器来生成精确完整的SVD，适合数据量比较适中，计算时 间充足的情况，生成的精确完整的SVD的结构为: U_(m,m) ,∑_(m,n) ,V_(n,n)
  arpack：从scipy.sparse.linalg.svds调用ARPACK分解器来运行截断奇异值分解(SVD truncated)，分解时就 将特征数量降到n_components中输入的数值k，可以加快运算速度，适合特征矩阵很大的时候，但一般用于 特征矩阵为稀疏矩阵的情况，此过程包含一定的随机性。截断后的SVD分解出的结构为：U_(m,k) ,∑_(m,k) ,V_(n,n)
  randomized：在"full"方法中，分解器会根据原始数据和输入的 n_components值去计算和寻找符合需求的新特征向量，但是在"randomized"方法中，分解器会先生成多个 随机向量，然后一一去检测这些随机向量中是否有任何一个符合我们的分解需求，如果符合，就保留这个随 机向量，并基于这个随机向量来构建后续的向量空间。这个方法已经被Halko等人证明，比"full"模式下计算快 很多，并且还能够保证模型运行效果。适合特征矩阵巨大，计算量庞大的情况。

• random_state：当svd_solver取值为arpack和randomized时的随机数种子

补充知识点：SVD

详细可戳svd.

2.2 重要属性

• components_：设降维后的特征矩阵为x_pca,即x * V的转置 = x_pca,components_就是V
  x的shape为(m,n),V的shape是(k,n),x_pca的shape是(m,k)

• explained_variance_:各主成分的可解释性方差

• explained_variance_ratio_:各主成分可解释性方差占比（分母是所有特征的方差和）

2.3 重要方法

• inverse_transform:将降维后的特征矩阵升维会原始的维度

from sklearn.datasets import fetch_lfw_people

faces = fetch_lfw_people(min_faces_per_person=60)

faces.data.shape #一共有1348张图，每张图2914个pixel

(1348, 2914)

faces.images.shape # 62*47=2914

(1348, 62, 47)

fig,axes = plt.subplots(4,4
                       ,figsize=(10,10)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('original pic',y=0.92,fontsize=15) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(faces.images[i,:,:],cmap='gray')    

ps:plt的cmap请戳plt的cmap.

# pca降维处理
pca = PCA(150).fit(faces.data) #原本有2914维，现在降成150维
v = pca.components_
v.shape

(150, 2914)

fig,axes = plt.subplots(15,10
                       ,figsize=(25,40)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('feature extraction',y=0.9,fontsize=20) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(v[i,:].reshape(62,47),cmap='gray')   
'''
我们可以把components_中的每一行看成一个特征提取器，本例中一共150行，使用v就可以从每张原始图片中提取150个特征出来，也就把2914维降到了150维
从下面对特征提取器的可视化可以看出，不同的提取器提取的是原始图片中不同的特征
比如前几个应该提取的是原始图片中的光线
后面几个可能提取的是五官
之后可能是面部表情
最后那些可能是脸部轮廓
'''

x_pca = pca.transform(faces.data)
x_pca.shape #原始特征矩阵变成了150维

(1348, 150)

x_inverse = pca.inverse_transform(x_pca)
x_inverse.shape

(1348, 2914)

fig,axes = plt.subplots(2,10
                       ,figsize=(25,7)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.text(0.5,0.89,'original pic',fontsize=20)
fig.text(0.5,0.48,'inverse pic',fontsize=20)
for i in range(10):
    axes[0][i].imshow(faces.images[i,:,:],cmap='gray')
    axes[1][i].imshow(x_inverse[i,:].reshape(62,47),cmap='gray')
'''
可以看出，通过升维复原的图片基本能反映原始图片的样子，但是略模糊。说明inverse_transform并没有实现数据的完全逆转
可以这样理解：x_pca是x通过丢掉部分信息所得到的，所以通过x_pca inverse_transform得到的x'不能包含x的全部信息
因此降维不是完全可逆的
'''

3.使用PCA降噪

从上面还原的图片来看，使用pca处理的图片虽然不能完全反应原始图片，但它保留了原始图片的重要特征

基于此，我们考虑使用pca提取原始数据中的重要特征，也就是剔除原始数据中的噪声

from sklearn.datasets import load_digits
load_digits().data.shape # 1797张图片，每个图片64个pixel

(1797, 64)

load_digits().images.shape #每个图片的size是8*8

(1797, 8, 8)

load_digits().target

array([0, 1, 2, ..., 8, 9, 8])

fig,axes = plt.subplots(4,4
                       ,figsize=(10,10)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('original pic',y=0.92,fontsize=15) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(load_digits().images[i,:,:],cmap='binary')
    ax.set_title(load_digits().target[i])

rng = np.random.RandomState(805)
noise = rng.normal(load_digits().images,2) #为每张图片的每个pixel生成噪声
x_with_noise = load_digits().images+noise

fig,axes = plt.subplots(4,4
                       ,figsize=(10,10)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('noise pic',y=0.92,fontsize=15) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(x_with_noise[i,:,:],cmap='binary')
    ax.set_title(load_digits().target[i])

# 使用pca提取原始图片中的重要特征
pca = PCA(0.85,svd_solver='full').fit(x_with_noise.reshape(x_with_noise.shape[0],-1)) 
x_pca = pca.transform(x_with_noise.reshape(x_with_noise.shape[0],-1))
x_pca.shape #即19个特征包含了原始特征矩阵85%的信息

(1797, 19)

# 通过inverse_transform得到降噪之后的图片
x_without_noise = pca.inverse_transform(x_pca).reshape(x_pca.shape[0],8,8)

fig,axes = plt.subplots(3,10
                       ,figsize=(25,7)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.text(0.5,0.9,'original pic',fontsize=15)
fig.text(0.5,0.63,'noise pic',fontsize=15)
fig.text(0.5,0.36,'without_noise pic',fontsize=15)
for i in range(10):
    axes[0][i].imshow(load_digits().images[i,:,:],cmap='binary')
    axes[1][i].imshow(x_with_noise[i,:,:],cmap='binary')
    axes[2][i].imshow(x_without_noise[i,:,:],cmap='binary')
    axes[2][i].set_title(load_digits().target[i],y=-0.2,fontsize=15)
'''
可以看出，降噪之后的图片将数字周围的噪声点模糊了许多
'''

如果上面的这个例子还不够清楚的话，请看下面这个例子

digit = pd.read_csv('digit recognizor.csv')
x = digit.iloc[:,1:]
y = digit.iloc[:,0]

fig,axes = plt.subplots(4,4
                       ,figsize=(10,10)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('original pic',y=0.92,fontsize=15) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(x.iloc[i,:].values.reshape(28,28),cmap='binary')
    ax.set_title(y[i])

rng = np.random.RandomState(805)
noise = rng.normal(x,100) #为每张图片的每个pixel生成噪声
x_with_noise = x+noise

fig,axes = plt.subplots(4,4
                       ,figsize=(10,10)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('noise pic',y=0.92,fontsize=15) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(x_with_noise.iloc[i,:].values.reshape(28,28),cmap='binary')
    ax.set_title(y[i])
# 可以看到，在数字周围生成了很多噪声点

# 使用pca提取原始图片中的重要特征
pca = PCA(0.5,svd_solver='full').fit(x_with_noise) 
x_pca = pca.transform(x_with_noise)
x_pca.shape #即35个特征包含了原始特征矩阵50%的信息

(42000, 35)

x_without_noise = pca.inverse_transform(x_pca)

fig,axes = plt.subplots(3,10
                       ,figsize=(25,7)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.text(0.5,0.9,'original pic',fontsize=15)
fig.text(0.5,0.63,'noise pic',fontsize=15)
fig.text(0.5,0.36,'without_noise pic',fontsize=15)
for i in range(10):
    axes[0][i].imshow(x.iloc[i,:].values.reshape(28,28),cmap='binary')
    axes[1][i].imshow(x_with_noise.iloc[i,:].values.reshape(28,28),cmap='binary')
    axes[2][i].imshow(x_without_noise[i,:].reshape(28,28),cmap='binary')
    axes[2][i].set_title(y[i],y=-0.2,fontsize=15)
'''
可以看出，降噪之后的图片保留了原始图片中数字部分的信息（绝大部分信息），而忽略了数字周围的噪声点
'''

4.使用PCA后对分类效果的影响

背景交代：手写数字识别，使用KNN准确率96%，但是要花半小时左右，即使使用过滤法提取一半特征之后，也要花费20分钟

使用RF准确率94%，耗时10s，经过特征选择、不断调参，能使准确率上到96%;

因此，虽然KNN准确率在毫无处理（不进行特征工程、不进行调参）的情况下较高,但由于太耗时，所以我们之前选择的是RF

而KNN耗时的原因就在于它要遍历所有特征（RF在建每一棵树时，是随机选取部分特征的），所以我们猜测使用PCA对原始特征矩阵降维之后，能使KNN花费时间减少

digit = pd.read_csv('digit recognizor.csv')
x = digit.iloc[:,1:]
y = digit.iloc[:,0]

fig,axes = plt.subplots(4,4
                       ,figsize=(10,10)
                       ,subplot_kw={'xticks':[],'yticks':[]}) #去掉所有子图的坐标
fig.suptitle('original pic',y=0.92,fontsize=15) #给整个画布加上一个总标题
for i,ax in enumerate(axes.flat):
    ax.imshow(x.iloc[i,:].values.reshape(28,28),cmap='binary')
    ax.set_title(y[i])

4.1 pca+rf

from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score

rfc = RFC(random_state=85,n_estimators=200)

x_score = cross_val_score(rfc,x,y,cv=5).mean() #使用全部特征
x_score

0.9659762754609975

pca = PCA().fit(x)

ex_var_ratio = pca.explained_variance_ratio_

len(ex_var_ratio)

784

plt.figure(figsize=(20,5))
plt.plot(np.cumsum(ex_var_ratio))
plt.axhline(y=0.85,c='r')
plt.text(150,0.8,'85%',fontsize=15)
plt.title('碎石图')
plt.show()
# 可以几十个特征就已经包含了85%的信息

pca_scores = []
for i in range(1,101,10):
    x_pca = PCA(i).fit_transform(x)
    pca_scores.append(cross_val_score(rfc,x_pca,y,cv=5).mean())

plt.figure(figsize=(20,5))
plt.plot(list(range(1,101,10)),pca_scores)
plt.scatter((pca_scores.index(max(pca_scores))+1)*10,max(pca_scores),c='r')
plt.text((pca_scores.index(max(pca_scores))+1)*10+0.5,max(pca_scores)-0.05,
         '({},{:.2f}):效果最好的点'.format((pca_scores.index(max(pca_scores))+1)*10,max(pca_scores)))
plt.show()
# 可以看到，降维到30时，取得了最好的效果，那么下一步我们进一步细化20~40这个区间

pca_scores = []
for i in range(20,41):
    x_pca = PCA(i).fit_transform(x)
    pca_scores.append(cross_val_score(rfc,x_pca,y,cv=5).mean())

plt.figure(figsize=(20,5))
plt.plot(list(range(20,41)),pca_scores)
plt.scatter(pca_scores.index(max(pca_scores))+20,max(pca_scores),c='r')
plt.text(pca_scores.index(max(pca_scores))+20,max(pca_scores)-0.0005,
         '({},{:.2f}):效果最好的点'.format(pca_scores.index(max(pca_scores))+20,max(pca_scores)))
plt.show()

x_pca = PCA(28).fit_transform(x)
cross_val_score(RFC(n_estimators=200,random_state=85),x_pca,y,cv=5).mean()
# 效果不如使用全部特征，但是时间减少很多
# 后续也可以通过继续调参使准确率提升，但这里就不再进行了
# 反正知道pca可以在使用很少的特征情况下，达到不错的效果

0.9486197900364252

4.2 pca+knn

from sklearn.neighbors import KNeighborsClassifier as KNN

cross_val_score(KNN(),x_pca,y,cv=5).mean()
# 可以看到,在KNN未进行调参的情况下，使用28个特征准确率已经达到了97%，
# 效果好于使用全部特征，并且时间只有40s!!!

0.9717138275521892

%%timeit
cross_val_score(KNN(),x_pca,y,cv=5).mean()

40.6 s ± 1.86 s per loop (mean ± std. dev. of 7 runs, 1 loop each)

import time
start_time = time.time()
knn_scores = []
for k in range(1,11):
    knn_scores.append(cross_val_score(KNN(k),x_pca,y,cv=5).mean())
end_time = time.time()
print('{:.2f}s'.format(end_time-start_time))

364.40s

plt.figure(figsize=(15,5))
plt.plot(list(range(1,11)),knn_scores)
plt.scatter(list(range(1,11))[knn_scores.index(max(knn_scores))],max(knn_scores),c='r')
plt.text(list(range(1,11))[knn_scores.index(max(knn_scores))]+0.06,max(knn_scores)-0.0003,'({},{:.2f})'.format(list(range(1,11))[knn_scores.index(max(knn_scores))],max(knn_scores)))
plt.show()
# 即n_neighbors=5时，分类效果最好，准确率达97%

因此使用pca+knn确实能在追求高准确率的同时，减少耗时。